 Backend Development
Backend Development
 PHP Tutorial
PHP Tutorial
 How to use PHP and GMP to test Fermat's theorem for large integers
How to use PHP and GMP to test Fermat's theorem for large integers
How to use PHP and GMP to test Fermat's theorem for large integers
How to use PHP and GMP to test Fermat's Little Theorem for large integers
Fermat's Little Theorem is one of the important theorems in number theory. It can be used to perform primality testing of large integers, that is, to determine whether a large integer is prime. In this article, we will introduce how to use PHP and the GMP extension library to perform testing of Fermat's Little Theorem for large integers.
First of all, we need to understand the principle of Fermat's theorem. Fermat's Little Theorem is expressed as follows:
If p is a prime number, a is any integer, and a is not divisible by p, then a^(p-1) ≡ 1 (mod p).
According to the Little Fermat Theorem, we can test the Little Fermat Theorem for large integers. The specific steps are as follows:
Step 1: Import the GMP extension library
Since PHP’s built-in functions cannot handle large integers, we need to import the GMP extension library to process large integers. In PHP, you can import the GMP extension library through the following code:
if (extension_loaded('gmp')) {
echo "GMP扩展库已加载。
";
} else {
echo "GMP扩展库未加载。
";
exit;
}Step 2: Implement the Little Fermat Theorem test function
We can implement the Little Fermat Theorem for large integers by defining a function test. The function is defined as follows:
function fermatTest($n, $k) {
for ($i = 0; $i < $k; $i++) {
$a = gmp_random_range(2, $n-1); // 随机选择一个整数a
$result = gmp_powm($a, $n-1, $n); // 计算 a^(n-1) mod n
if (gmp_cmp($result, 1) !== 0) { // 如果结果不等于1,则n不是素数
return false;
}
}
return true; // 如果所有测试都通过,则n可能是素数
}In the above code, we use the gmp_random_range function to generate a random integer $a$ between 2 and $n-1$, and then use the gmp_powm function to calculate $a^ The result of {n-1} mod n$. If the result is not equal to 1, then $n$ is not a prime number and returns false; otherwise, continue with the next test. If all tests pass, then $n$ is probably prime, return true.
Step 3: Test function
We can write a test function to verify the correctness of the implemented Little Fermat Theorem test function. The test function is defined as follows:
function testFermatTest($n) {
if (fermatTest($n, 10)) { // 进行10次小费马定理测试
echo "{$n} 可能是素数。
";
} else {
echo "{$n} 不是素数。
";
}
}In the above code, we call the fermatTest function to test Fermat's theorem 10 times, and then output the corresponding information based on the test results.
Step 4: Execute the test
Finally, we can call the test function to perform the little Fermat theorem test. For example, we can test a larger integer 100000000000000000003 with the following code:
testFermatTest(gmp_init("100000000000000000003"));In the above code, we use the gmp_init function to convert the string "100000000000000000003" into a large integer, and then perform the Fermat theorem test.
Through the above steps, we can use PHP and GMP extension libraries to test the small Fermat theorem of large integers. This is a simple yet effective method for determining whether a large integer is prime.
Please note that in practical applications, Fermat's Theorem test is often combined with other testing methods to improve the accuracy and reliability of the test.
The above is the detailed content of How to use PHP and GMP to test Fermat's theorem for large integers. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 CakePHP Project Configuration
Sep 10, 2024 pm 05:25 PM
CakePHP Project Configuration
Sep 10, 2024 pm 05:25 PM
In this chapter, we will understand the Environment Variables, General Configuration, Database Configuration and Email Configuration in CakePHP.
 PHP 8.4 Installation and Upgrade guide for Ubuntu and Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 Installation and Upgrade guide for Ubuntu and Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 brings several new features, security improvements, and performance improvements with healthy amounts of feature deprecations and removals. This guide explains how to install PHP 8.4 or upgrade to PHP 8.4 on Ubuntu, Debian, or their derivati
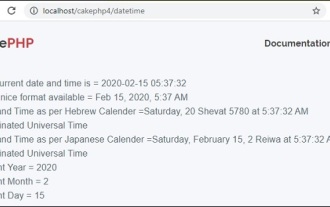 CakePHP Date and Time
Sep 10, 2024 pm 05:27 PM
CakePHP Date and Time
Sep 10, 2024 pm 05:27 PM
To work with date and time in cakephp4, we are going to make use of the available FrozenTime class.
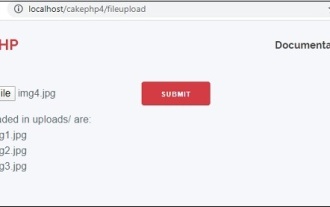 CakePHP File upload
Sep 10, 2024 pm 05:27 PM
CakePHP File upload
Sep 10, 2024 pm 05:27 PM
To work on file upload we are going to use the form helper. Here, is an example for file upload.
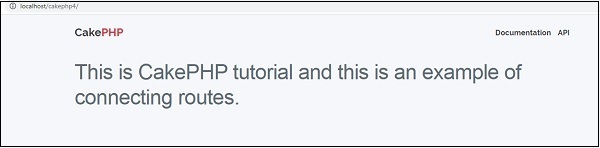 CakePHP Routing
Sep 10, 2024 pm 05:25 PM
CakePHP Routing
Sep 10, 2024 pm 05:25 PM
In this chapter, we are going to learn the following topics related to routing ?
 Discuss CakePHP
Sep 10, 2024 pm 05:28 PM
Discuss CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP is an open-source framework for PHP. It is intended to make developing, deploying and maintaining applications much easier. CakePHP is based on a MVC-like architecture that is both powerful and easy to grasp. Models, Views, and Controllers gu
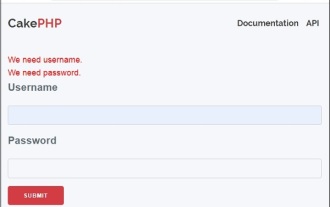 CakePHP Creating Validators
Sep 10, 2024 pm 05:26 PM
CakePHP Creating Validators
Sep 10, 2024 pm 05:26 PM
Validator can be created by adding the following two lines in the controller.
 How To Set Up Visual Studio Code (VS Code) for PHP Development
Dec 20, 2024 am 11:31 AM
How To Set Up Visual Studio Code (VS Code) for PHP Development
Dec 20, 2024 am 11:31 AM
Visual Studio Code, also known as VS Code, is a free source code editor — or integrated development environment (IDE) — available for all major operating systems. With a large collection of extensions for many programming languages, VS Code can be c





