Drawing Bezier curves using canvas_html5 tutorial tips

1. Quadratic Bezier Curve

QuadraticCurveTo(cpx,cpy,x,y) //cpx, cpy represents the coordinates of the control point, x, y represents the end point coordinates;

The mathematical formula is expressed as follows:

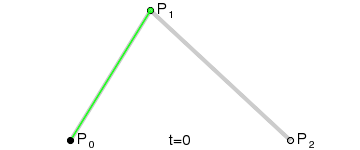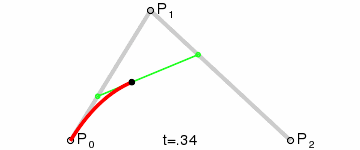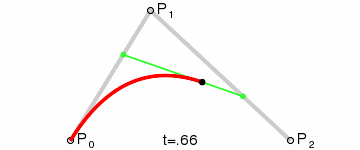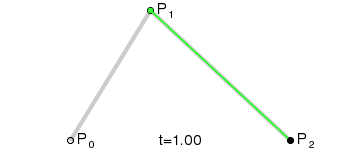
The path of the quadratic Bezier curve is traced by the function B (t) given the points P0, P1, P2:

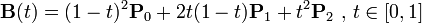
Code example:

Copy code

The code is as follows:

<script><br> function draw() {<br> var canvas=document.getElementById('canvas');<br> var context=canvas.getContext('2d');<br> //Drawing starting point , control point, end point <br> context.beginPath(); <br> context.moveTo(20,170); <br> context.lineTo(130,40); <br> context.lineTo(180,150); <br> context .stroke(); </p> <p> //Draw a quadratic Bezier curve <br> context.beginPath(); <br> context.moveTo(20,170); <br> context.quadraticCurveTo(130,40,180,150); <br> context.strokeStyle = "red"; <br> context.stroke(); <br>}<br></script>

Code effect:

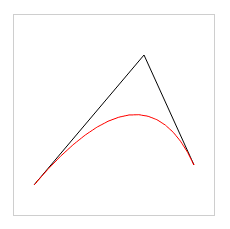
2. Cubic Bezier Curve

BezierCurveTo(cp1x,cp1y,cp2x,cp2y,x,y) //cp1x, cp1y represents the coordinates of the first control point, cp2x, cp2y represents the coordinates of the second control point, x, y represents the coordinates of the end point ;

The mathematical formula is expressed as follows:

The four points P0, P1, P2, and P3 define a cubic Bezier curve on a plane or in a three-dimensional space. The curve starts from P0 and goes to P1, and from the direction of P2 to P3. Generally it will not pass through P1 or P2; these two points are just there to provide directional information. The distance between P0 and P1 determines "how long" the curve goes in the direction of P2 before turning towards P3.

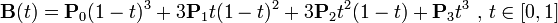
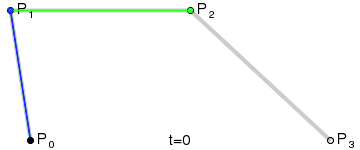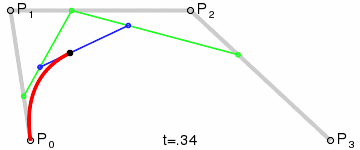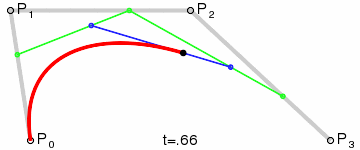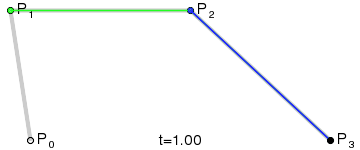
Code example:

Copy code

The code is as follows:

three times Bezier curve

function draw() {
var canvas=document.getElementById('canvas');
var context=canvas.getContext('2d');
//Draw starting point, control point , end point
context.beginPath();
context.moveTo(25,175);
context.lineTo(60,80);
context.lineTo(150,30);
context. lineTo(170,150);
context.stroke();

//Draw a cubic Bezier curve
context.beginPath();
context.moveTo(25,175);
context.bezierCurveTo(60,80,150,30,170,150);
context .strokeStyle = "red";
context.stroke();
}

Code rendering:

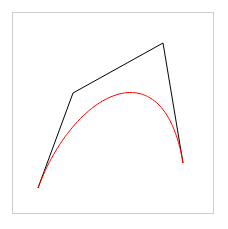
Isn’t it a cool effect? . . HTML5 canvas is really a fun thing, addictive.