 Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 Python program to calculate the sum of the right diagonal elements of a matrix
Python program to calculate the sum of the right diagonal elements of a matrix
Python program to calculate the sum of the right diagonal elements of a matrix

A popular general-purpose programming language is Python. It is used in a variety of industries, including desktop applications, web development, and machine learning. Fortunately, Python has a simple and easy-to-understand syntax that is suitable for beginners. In this article, we will use Python to calculate the sum of the right diagonal of a matrix.
What is a matrix?
In mathematics, we use a rectangular array or matrix to describe a mathematical object or its properties. It is a rectangular array or table containing numbers, symbols, or expressions arranged in rows. and column arrangement.
For example −
2 3 4 5 1 2 3 6 7 5 7 4
So, this is a matrix with 3 rows and 4 columns, expressed as a 3*4 matrix.
Now, there are two diagonals in the matrix, the main diagonal and the sub-diagonal. The main diagonal is the diagonal line from the upper left corner to the lower right corner, and the secondary diagonal is the diagonal line from the lower left corner to the upper right corner.
We can see from the above example that a00 and a11 are both main diagonals (left diagonals), while a10 and a01 are secondary diagonals (right diagonals), as shown below
2 3 a<sub>00</sub> a<sub>01</sub> 1 2 a<sub>10</sub> a<sub>11</sub>
Sum of right diagonal of matrix
Since we have revised the basic concepts and have a complete understanding of matrices and diagonals, let us now delve deeper into the topic and complete the coding part of the concept.
To calculate the sum, we can use a 2D matrix. Consider a 4*4 matrix whose elements are
Here, a00, a11, a22 and a33 are the main diagonal elements of the matrix. The subdiagonal consists of elements a30, a21, a12 and a03.
Before completing this task, there is an important condition to consider: in order to take the sum of the elements on the main diagonal, it must satisfy the so-called row and column conditions, that is, each element in each row must have a Equal column numbers.
Similarly, for calculating the sum of elements on the sub-diagonal (a03, a12, a21 and a30), the row and column conditions will be equal to the number of rows minus the number of columns minus 1.
2 4 6 8 a00 a01 a02 a03 3 5 7 9 a10 a11 a12 a13 1 4 6 7 a20 a21 a22 a23 3 5 1 4 a30 a31 a32 a33
Use For Loop
In this method we will use two loops, one for rows and columns and another to check the condition we provide.
algorithm
Give a value, which is the maximum value.
Define a function for the matrix.
Use a for loop to iterate over numbers
Provide conditions for the right diagonal of the matrix.
Print this value.
Example
This example defines a constant MAX with a value of 50, and then creates a function called SUM_RIGHT_MATRIX that accepts a matrix and an integer as parameters.
This function adds all the numbers on the right diagonal of the given matrix (i.e. from the upper right corner to the lower left corner) and prints out the sum.
MAX = 50
def SUM_RIGHT_MATRIX (matrix, m):
rightD = 0;
for i in range (0, m):
for j in range (0, m):
if ((i + j) == (m - 1)):
rightD += matrix[i][j]
print ("Sum of right diagonal is:", rightD)
T = [[ 13, 21, 33, 45 ],
[ 52, 16, 27, 28 ],
[ 17, 28, 31, 43 ],
[ 54, 26, 87, 28 ]]
SUM_RIGHT_MATRIX (T, 4)
Output
After executing the above program, we get "The sum of the right diagonals is: 155". This means the sum of all the numbers on the right diagonal is 155.
Sum of right diagonal is: 154
Use a single loop
Using this method, the sum of the main diagonal and the sub-diagonal is calculated through a loop.
algorithm
Give a value, which is the maximum value.
Define a function for the matrix.
Use a for loop to iterate over numbers.
Provide conditions for the right diagonal of the matrix.
Print this value.
Example
The following example defines a function named sumofrightdiagonal that accepts two parameters: a matrix and m.
It loops through the matrix and adds each number on the right diagonal of the matrix, storing them in a variable called right_diagonal.
Finally, it prints "Sum of Right Diagonal is:", followed by the value stored in right_diagonal. The example also includes an input example T (a 4x4 matrix) where m equals 4, so when Sumofrightdiagonal is called with these values as arguments, it will calculate and print out the sum of all elements on the right diagonal of T.
MAX = 50
def sumofrightdiagonal (matrix, m):
right_diagonal = 0
for i in range (0, m):
right_diagonal += matrix [i] [m - i - 1]
print ("Sum of Right Diagonal is:", right_diagonal)
T = [[ 11, 12, 33, 24 ],
[ 54, 69, 72, 84 ],
[ 14, 22, 63, 34 ],
[ 53, 64, 79, 83 ]]
sumofrightdiagonal (T, 4)
Output
Sum of Right Diagonal: 171
in conclusion
In this article, we briefly discussed two simple ways to calculate the right diagonal sum of a matrix using Python programs. The first method uses two loops to accomplish the task we provided, while the second method provides a more efficient way to accomplish the same task, but with a shorter path.
The above is the detailed content of Python program to calculate the sum of the right diagonal elements of a matrix. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
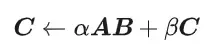 CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) is a vital part of many applications and algorithms, and is also one of the important indicators for evaluating computer hardware performance. In-depth research and optimization of the implementation of GEMM can help us better understand high-performance computing and the relationship between software and hardware systems. In computer science, effective optimization of GEMM can increase computing speed and save resources, which is crucial to improving the overall performance of a computer system. An in-depth understanding of the working principle and optimization method of GEMM will help us better utilize the potential of modern computing hardware and provide more efficient solutions for various complex computing tasks. By optimizing the performance of GEMM
 How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
WORD is a powerful word processor. We can use word to edit various texts. In Excel tables, we have mastered the calculation methods of addition, subtraction and multipliers. So if we need to calculate the addition of numerical values in Word tables, How to subtract the multiplier? Can I only use a calculator to calculate it? The answer is of course no, WORD can also do it. Today I will teach you how to use formulas to calculate basic operations such as addition, subtraction, multiplication and division in tables in Word documents. Let's learn together. So, today let me demonstrate in detail how to calculate addition, subtraction, multiplication and division in a WORD document? Step 1: Open a WORD, click [Table] under [Insert] on the toolbar, and insert a table in the drop-down menu.
 How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to use Python's count() function to calculate the number of an element in a list requires specific code examples. As a powerful and easy-to-learn programming language, Python provides many built-in functions to handle different data structures. One of them is the count() function, which can be used to count the number of elements in a list. In this article, we will explain how to use the count() function in detail and provide specific code examples. The count() function is a built-in function of Python, used to calculate a certain
 Exploring the History and Matrix of Artificial Intelligence: Artificial Intelligence Tutorial (2)
Nov 20, 2023 pm 05:25 PM
Exploring the History and Matrix of Artificial Intelligence: Artificial Intelligence Tutorial (2)
Nov 20, 2023 pm 05:25 PM
In the first article of this series, we discussed the connections and differences between artificial intelligence, machine learning, deep learning, data science, and more. We also made some hard choices about the programming languages, tools, and more that the entire series would use. Finally, we also introduced a little bit of matrix knowledge. In this article, we will discuss in depth the matrix, the core of artificial intelligence. But before that, let’s first understand the history of artificial intelligence. Why do we need to understand the history of artificial intelligence? There have been many AI booms in history, but in many cases the huge expectations for AI's potential failed to materialize. Understanding the history of artificial intelligence can help us see whether this wave of artificial intelligence will create miracles or is just another bubble about to burst. us
 Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Given two strings str_1 and str_2. The goal is to count the number of occurrences of substring str2 in string str1 using a recursive procedure. A recursive function is a function that calls itself within its definition. If str1 is "Iknowthatyouknowthatiknow" and str2 is "know" the number of occurrences is -3. Let us understand through examples. For example, input str1="TPisTPareTPamTP", str2="TP"; output Countofoccurrencesofasubstringrecursi
 How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
In C#, there is a Math class library, which contains many mathematical functions. These include the function Math.Pow, which calculates powers, which can help us calculate the power of a specified number. The usage of the Math.Pow function is very simple, you only need to specify the base and exponent. The syntax is as follows: Math.Pow(base,exponent); where base represents the base and exponent represents the exponent. This function returns a double type result, that is, the power calculation result. Let's
 Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Introduction The Java program for calculating the area of a triangle using determinants is a concise and efficient program that can calculate the area of a triangle given the coordinates of three vertices. This program is useful for anyone learning or working with geometry, as it demonstrates how to use basic arithmetic and algebraic calculations in Java, as well as how to use the Scanner class to read user input. The program prompts the user for the coordinates of three points of the triangle, which are then read in and used to calculate the determinant of the coordinate matrix. Use the absolute value of the determinant to ensure the area is always positive, then use a formula to calculate the area of the triangle and display it to the user. The program can be easily modified to accept input in different formats or to perform additional calculations, making it a versatile tool for geometric calculations. ranks of determinants
 Python program to multiply two matrices using multidimensional arrays
Sep 11, 2023 pm 05:09 PM
Python program to multiply two matrices using multidimensional arrays
Sep 11, 2023 pm 05:09 PM
A matrix is a set of numbers arranged in rows and columns. A matrix with m rows and n columns is called an mXn matrix, and m and n are called its dimensions. A matrix is a two-dimensional array created in Python using lists or NumPy arrays. In general, matrix multiplication can be done by multiplying the rows of the first matrix by the columns of the second matrix. Here, the number of columns of the first matrix should be equal to the number of rows of the second matrix. Input and output scenario Suppose we have two matrices A and B. The dimensions of these two matrices are 2X3 and 3X2 respectively. The resulting matrix after multiplication will have 2 rows and 1 column. [b1,b2][a1,a2,a3]*[b3,b4]=[a1*b1+a2*b2+a3*a3][a4,a5,a6][b5,b6][a4*b2+a



