Meituan interview: Please handwrite a quick schedule, I was shocked!

Today, this question was asked by the interviewer to quickly arrange it by handwriting on the spot. The scene is as follows:

Interviewer: Let’s continue chatting. Regarding data structures and algorithms, can you write a quick sort? (While speaking, he turned my resume over and handed me a pen, meaning he asked me to write on the back of my resume)

Rookie Me: What do you mean? Write it here? (Pointing to the resume)

Interviewer: Yeah

Rookie Me: No

Interviewer: Okay, that’s all for today’s interview

Rookie Me: (I’m very angry. It’s a labor-management resume. Do you want to write code on the labor-management resume?) Shadiao

Interviewer: (Looking back, confused)

Thinking about it, I was still too young, but that wouldn't be the case now. Just write, it’s just a piece of paper anyway.

Actually, quick queuing is simple, but I guess many people can’t write it by hand. Is it difficult? There are many people who can write it by hand on the spot in several ways.

I am a newbie, but I can still write by hand. After all, I just deliberately prepared "dictate writing" before the interview.

Next, we will analyze and analyze ---- quick sort.

Background

From encyclopedia:

Quick sort was proposed by C. A. R. Hoare in 1962. Its basic idea is to divide the data to be sorted into two independent parts through one sorting. All the data in one part is smaller than all the data in the other part, and then use this method to quickly separate the two parts of the data. Sorting, the entire sorting process can be performed [recursively], so that the entire data becomes an ordered sequence.

It is quite difficult to understand this concept.

It can be understood this way:

Quick sort is an improved version of bubble sort. The whole process is to tear things apart and patch them up. Complement side by side until all elements reach an ordered state.

Core idea:

First take a number from the sequence as the base number, and then perform size partitioning;

During the partitioning process, compare this number Place all large numbers to its right, and put all numbers less than or equal to it to its left;

Repeat the second step for the left and right intervals until there is only one number in each interval, and the sorting is completed.

Implementation case

The following is a step-by-step disassembly in the form of pictures and texts.

Take the array [4,1,6,2,9,3] as an example.

First pass:

• First split [4,1,6,2,9,3] and select element 4 as the pivot point
• Check whether 1 < 4 (pivot point)
• Check if 6 < 4 (pivot point)
• Check if 2 < 4 (pivot point) Point)
• ##2 < 4 (pivot point) is true, exchange index 2 and stored index 6
• Check if 9 < 4 (pivot point)
##Check if 3 < 4 (pivot point)
• ##3 < 4 (axis center point) is true, exchange index 3 and storage index 6
• Exchange pivot point 4 and storage index 3
• At this time, the left side of pivot point 4 is less than 4, and the right side is greater than 4

The current array sequence is [3, 1, 2, 4, 9, 6].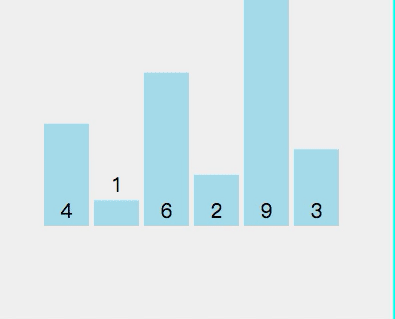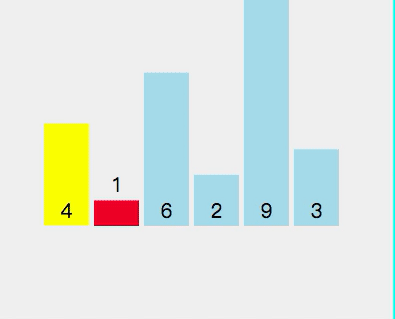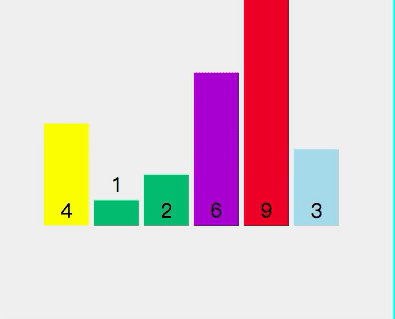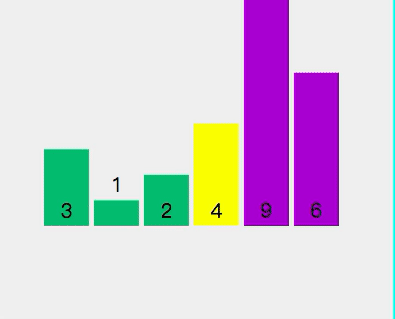

Next step:

Sort the left side first

• ##Select element 3 as the pivot point
• Check if 1 < 3 (pivot point)
• Check if 2 < 3 (pivot point)
• Exchange pivot point 3 and storage index value 2
• The pivot point is now at the sorted position
• Split [2,1] and select 2 as the pivot point
• Check whether 1 < 2 (pivot point)
• ## The traversal on the left is completed, and the pivot point 2 and the storage index 1 are exchanged.
• The same is true for the right... I will not describe them one by one to avoid visual fatigue. You can see the dynamic demonstration picture below.

2. The whole process of quick sorting

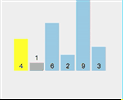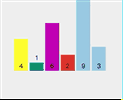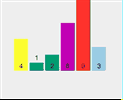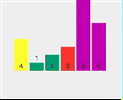
3. Code implementation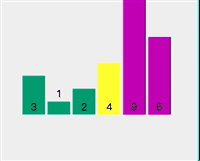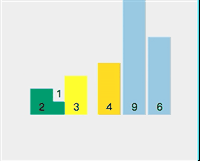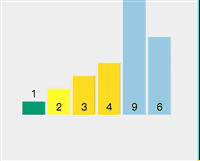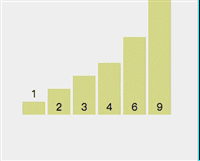

Below, we use Java language to implement the previous quick sort case:

import java.util.Arrays;

public class QuickSortDemo {
    //四个步骤：
    //1.比较startIndex和endIndex，更喜欢理解为校验
    //2.找出基准
    //3.左边部分排序
    //4.右边排序
    public static void quickSort(int[] arr, int startIndex, int endIndex) {
        if (startIndex < endIndex) {
            //找出基准
            int partition = partition(arr, startIndex, endIndex);
            //分成两边递归进行
            quickSort(arr, startIndex, partition - 1);
            quickSort(arr, partition + 1, endIndex);
        }
    }

    //找基准
    private static int partition(int[] arr, int startIndex, int endIndex) {
        int pivot = arr[startIndex];
        
        int left = startIndex;
        int right = endIndex;
        
        //等于就没有必要排序
        while (left != right) {
            
            while (left < right && arr[right] > pivot) {
                right--;
            }
          
            while (left < right && arr[left] <= pivot) {
                left++;
            }
            //找到left比基准大，right比基准小，进行交换
            if (left < right) {
                swap(arr, left, right);
            }
        }
        //第一轮完成，让left和right重合的位置和基准交换，返回基准的位置
        swap(arr, startIndex, left);
        return left;
    }

    //两数交换
    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] a = {3, 1, 2, 4, 9, 6};
        quickSort(a, 0, a.length - 1);
        //输出结果
        System.out.println(Arrays.toString(a));
    }
}

Output result:

[1, 2, 3, 4, 6, 9]

Code implementation, it is recommended to combine it with the previous animation to make it easier to understand.

There are several ways to write quick sort. If you are interested, you can look it up yourself. You can also look at how quick sort is introduced in Wikipedia.

4. Complexity analysis

Time complexity:

Worst The situation is that the element taken each time is the smallest/largest in the array. This situation is actually bubble sorting (the order of one element is arranged every time)

The time complexity in this case is good Calculated, it is the time complexity of bubble sort: T[n] = n * (n-1) = n^2 n;

The best case is O(nlog2n), derivation The process is as follows:

(Time complexity formula of recursive algorithm: T[n] = aT[n/b] f(n) )

https://img2018.cnblogs.com/blog/1258817/201903/1258817-20190326191158640-601403776.png

So The average time complexity is O(nlog2n)

Space complexity:

The space used by quick sort is O(1), which is a constant level; what really consumes space is the recursive call. Because some data must be maintained for each recursion:

The space complexity in the optimal case is: O(log2n); when the group is divided equally every time

The worst case space complexity is: O(n); it degenerates into bubble sorting

So the average space complexity is O(log2n)

5. Summary of quick sorting method

• The first element is taken as the pivot point by default (pivot point The confirmation distinguishes two algorithms: "quick sorting method" and "random sorting method"), and random sorting randomly rands an element as the pivot point;
• If the two are not consistent Neighbor element exchange can eliminate multiple reverse orders in one exchange and speed up the sorting process.

Postscript

Finally, do you think quick sort is useful at work? ? I have never used it after working for nearly ten years, but I know the idea of ​​​​quick queue. If I don’t prepare before the interview, I definitely won’t be able to write it anyway. What about you?

The above is the detailed content of Meituan interview: Please handwrite a quick schedule, I was shocked!. For more information, please follow other related articles on the PHP Chinese website!