 Backend Development
Backend Development
 C++
C++
 Write a program in C language to print out a sequence of N pentagonal numbers
Write a program in C language to print out a sequence of N pentagonal numbers
Write a program in C language to print out a sequence of N pentagonal numbers
Program description
The five-dimensional number is the fifth number in any row of Pascal's triangle, starting from left to right or right to left, starting from the 5-term row 1 4 6 4 1.
The first few numbers of this kind are
1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, 1365
Pentatope numbers belong in the class of figurate numbers, which can be represented as regular, discrete geometric patterns. The formula for the nth pentatopic number is
$$\left(\begin{array}{c}n 3\ 4\end{array}\right)=\left(\frac{n(n 1) ( n 2) (n 3)}{24}\right)=\left(\frac{n^2}{4!}\right)$$
Algorithm
Accept the Nth Term from the User to find the Pentotope Numbers.
Use the formula
$$\left(\begin{array}{c}n 3\ 4\end{array}\right) =\left(\frac{n(n 1) (n 2) (n 3)}{24}\right)=\left(\frac{n^2}{4!}\right)$$
Example
/* Program to print pentatope numbers upto Nth term */
#include<stdio.h>
int main() {
int n, n1, nthterm, nthterm1, i;
clrscr();
printf("</p><p> Please enter the nth term to print Pentatope: ");
scanf("%d",&n);
nthterm = n * (n + 1) * (n + 2) * (n + 3) / 24;
printf("The Pentotpe Number is: ");
printf("%d", nthterm);
printf("</p><p></p><p>");
printf("Printing the Pentotope Numbers upto Nth Term");
printf("</p><p> Print Pentatope Numbers till the term: ");
scanf("%d",&n1);
printf("</p><p></p><p>");
printf("The Pentotope Numbers are:");
printf("</p><p></p><p>");
for (i = 1; i <= n1; i++){
nthterm1 = (i * (i + 1) * (i + 2) * (i + 3) / 24);
printf("%d\t", nthterm1);
}
getch();
return 0;
}Output
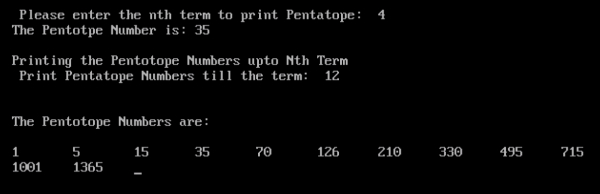
The above is the detailed content of Write a program in C language to print out a sequence of N pentagonal numbers. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1389
1389
 52
52
 What should I do if the frame line disappears when printing in Excel?
Mar 21, 2024 am 09:50 AM
What should I do if the frame line disappears when printing in Excel?
Mar 21, 2024 am 09:50 AM
If when opening a file that needs to be printed, we will find that the table frame line has disappeared for some reason in the print preview. When encountering such a situation, we must deal with it in time. If this also appears in your print file If you have questions like this, then join the editor to learn the following course: What should I do if the frame line disappears when printing a table in Excel? 1. Open a file that needs to be printed, as shown in the figure below. 2. Select all required content areas, as shown in the figure below. 3. Right-click the mouse and select the "Format Cells" option, as shown in the figure below. 4. Click the “Border” option at the top of the window, as shown in the figure below. 5. Select the thin solid line pattern in the line style on the left, as shown in the figure below. 6. Select "Outer Border"
 Insufficient memory or disk space to repagin or print this document Word error
Feb 19, 2024 pm 07:15 PM
Insufficient memory or disk space to repagin or print this document Word error
Feb 19, 2024 pm 07:15 PM
This article will introduce how to solve the problem of insufficient memory or disk space to repage or print the document in Microsoft Word. This error usually occurs when users try to print a Word document. If you encounter a similar error, please refer to the suggestions provided in this article to resolve it. Insufficient memory or disk space to repage or print this document Word error How to resolve the Microsoft Word printing error "There is not enough memory or disk space to repage or print the document." Update Microsoft Office Close memory-hogging applications Change your default printer Start Word in safe mode Rename the NorMal.dotm file Save the Word file as another
 4 Ways to Print from iPhone
Feb 02, 2024 pm 04:10 PM
4 Ways to Print from iPhone
Feb 02, 2024 pm 04:10 PM
In this digital world, the need for printed pages has not disappeared. While you might think it's more convenient to save content on your computer and send it directly to the printer, you can do the same thing on your iPhone. With your iPhone's camera, you can take a photo or document, and you can also store the file directly for printing at any time. This way you can quickly and easily materialize the information you need and save it in a paper document. Whether at work or in daily life, iPhone provides you with a portable printing solution. The following post will help you understand everything you need to know if you wish to use your iPhone to print pages on a printer. Print from iPhone: Ask Apple
 Can't print from snipping tool in Windows 11/10
Feb 19, 2024 am 11:39 AM
Can't print from snipping tool in Windows 11/10
Feb 19, 2024 am 11:39 AM
If you are unable to print using the Snipping Tool in Windows 11/10, it may be caused by corrupted system files or driver issues. This article will provide you with solutions to this problem. Can't print from Snipping Tool in Windows 11/10 If you can't print from Snipping Tool in Windows 11/10, use these fixes: Restart PC Printer Clear print queue Update printer and graphics driver Fix or reset Snipping Tool Run SFC and DISM Scan uses PowerShell commands to uninstall and reinstall Snipping Tool. let us start. 1] Restart your PC and printer Restarting your PC and printer helps eliminate temporary glitches
 How to pause printing in Windows 11
Feb 19, 2024 am 11:50 AM
How to pause printing in Windows 11
Feb 19, 2024 am 11:50 AM
Printed a large file by mistake? Need to stop or pause printing to save ink and paper? There are many situations where you may need to pause an ongoing print job on your Windows 11 device. How to pause printing in Windows 11? In Windows 11, pausing printing will pause the print job, but it will not cancel the print task. This provides users with more flexible control. There are three ways to do this: Pause printing using the taskbar Pausing printing using Windows Settings Printing using the control panel Now, let’s look at these in detail. 1] Print using taskbar Right-click the print queue notification on the taskbar. Click to open all active printer options. Here, right-click on the print job and select Pause All
 Word mail merge prints blank page
Feb 19, 2024 pm 04:51 PM
Word mail merge prints blank page
Feb 19, 2024 pm 04:51 PM
If you find that blank pages appear when printing a mail merge document using Word, this article will help you. Mail merge is a convenient feature that allows you to easily create personalized documents and send them to multiple recipients. In Microsoft Word, the mail merge feature is highly regarded because it helps users save time manually copying the same content for each recipient. In order to print the mail merge document, you can go to the Mailings tab. But some Word users have reported that when trying to print a mail merge document, the printer prints a blank page or doesn't print at all. This may be due to incorrect formatting or printer settings. Try checking the document and printer settings and make sure to preview the document before printing to ensure the content is correct. if
 How to print all attachments in Outlook
Feb 20, 2024 am 10:30 AM
How to print all attachments in Outlook
Feb 20, 2024 am 10:30 AM
Outlook is one of the most feature-rich email clients and has become an indispensable tool for professional communication. One of the challenges is printing all attachments at the same time in Outlook. Usually you need to download attachments one by one before you can print them, but if you want to print everything at once, this is the problem most people encounter. How to Print All Attachments in Outlook Although most of the information is maintained online in the Outlook application, there are times when you need to print out the information for backup. Must sign documents in person to satisfy legal requirements such as contracts, government forms, or homework assignments. There are several methods that allow you to print all attachments in Outlook with one click instead of printing them one by one. Let's look at each one in detail. Outloo
 How to implement printing function in Vue
Nov 07, 2023 pm 12:33 PM
How to implement printing function in Vue
Nov 07, 2023 pm 12:33 PM
How to implement printing functionality in Vue requires specific code examples Vue.js is a progressive JavaScript framework for building user interfaces. In many web applications, printing functionality is a very important part. This article will introduce how to implement the printing function in Vue and provide specific code examples. To implement the printing function in Vue, you must first clarify what the printed content is. Usually, we will put the content to be printed in an HTML element, such as a div. Then, via Jav



