
A synchronization method called Lamport's Bakery method solves the critical section problem in parallel computing systems. When multiple processes need to use a shared resource simultaneously but only one process can do so, this is called a critical section problem. To avoid conflicts and guarantee system accuracy, the challenge is to ensure that each process uses resources in a mutually exclusive manner.
Here is the pseudocode of Lamport’s baking algorithm -
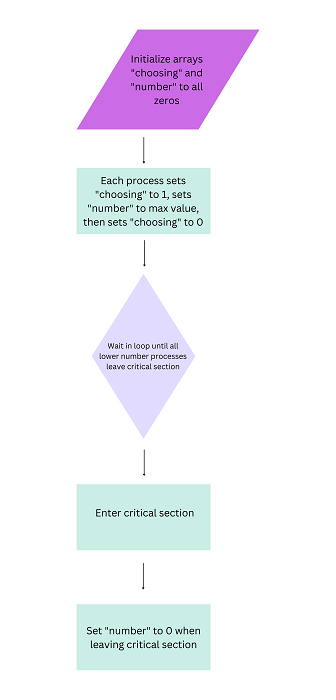
Initialize an array (called "select") of size N, where N is the total number of processes, to all zeros.
Initialize an array, called number, of size N, all zeros.
Each process i will execute the following code when it wants to enter the critical section -
Set selection[i] = 1
Set number[i] = max(number[0], number[1], ..., number[N-1]) 1
Set selection[i] = 0
For each other process j, repeat until (number[j] == 0) or (number[i], i)
Enter the key part
Each process i will execute the following code when leaving the critical section -
Set number[i] = 0
Here is a piece of code explaining the practical application of Lamport's baking algorithm. We will use C as the implementation language in this example.
#include <iostream>
#include <atomic>
#include <thread>
#define N 5
// total number of processes
using namespace std;
atomic<bool> entering[N] = {false};
// to keep track of which process is currently trying to enter critical section
atomic<int> number[N] = {0};
// to hold the ticket number for each process
void process(int i) {
while (true) {
// Step 1: Get ticket number
entering[i] = true;
int max_number = 0;
for (int j = 0; j < N; j++) {
if (number[j] > max_number) {
max_number = number[j];
}
}
number[i] = max_number + 1;
entering[i] = false;
// Step 2: Wait until it is this process's turn to enter the critical section
for (int j = 0; j < N; j++) {
while (entering[j]) {}
// wait until process j has finished choosing its ticket number
while ((number[j] != 0) && ((number[j] < number[i]) || ((number[j] == number[i]) && j < i))) {}
// busy wait until it is this process's turn to enter the critical section
}
// Step 3: Enter the critical section
cout << "Process " << i << " enters the critical section." << endl;
// perform critical section operations here
// Step 4: Exit the critical section
number[i] = 0;
cout << "Process " << i << " exits the critical section." << endl;
// perform remainder section operations here
}
}
int main() {
// create threads for each process
thread t[N];
for (int i = 0; i < N; i++) {
t[i] = thread(process, i);
}
// join threads
for (int i = 0; i < N; i++) {
t[i].join();
}
return 0;
}
Process 0 enters the critical section. Process 0 exits the critical section. Process 1 enters the critical section. Process 1 exits the critical section. Process 2 enters the critical section. Process 2 exits the critical section. Process 3 enters the critical section. Process 3 exits the critical section. Process 0 enters the critical section. Process 0 exits the critical section. Process 1 enters the critical section. Process 1 exits the critical section. Process 4 enters the critical section. Process 4Process exits the critical section.2 .............
The advantages of Lamport’s baking algorithm are listed below -
Fairness is ensured by providing different tokens to processes or threads requesting access to shared resources.
Distributing tokens based on specified values prevents starvation.
Use token-based strategies that are simple and easy to understand and execute.
Efficient and does not require complex data structures or inter-process interactions.
It provides mutual exclusion without specialized hardware or hardware assistance.
It has a wide range of applications and strong adaptability. It can be applied to a variety of different scenarios to ensure fairness and mutual exclusion of concurrent calculations.
A useful tool for software engineers working on distributed or parallel systems.
Busy Wait - This algorithm calls busy wait, which can lead to inefficiency and high CPU utilization, especially when there are a large number of processes or threads competing for access to the same shared resource.
hunger - Although the algorithm ensures justice, there are no safeguards. Occasionally, a process or thread may be repeatedly stopped, which prevents it from obtaining a token and accessing resources.
Overhead - This algorithm requires more memory and processing time to determine the token sequence because it requires storing state information for each process or thread.
Complexity - Application of the algorithm can be difficult because it must carefully handle race conditions and deadlocks, and may use synchronization mechanisms such as mutexes or semaphores.
李>A mutually exclusive algorithm called Lamport's baking algorithm ensures that individual processes or threads can take advantage of shared resources without interfering with each other. It's a simple algorithm that prevents starvation and ensures justice.
The algorithm works by assigning a token to each process or thread that makes a resource access request, and then comparing the values of these tokens to determine the order in which they were given. The resource is available first to operations with the fewest tokens.
The above is the detailed content of Lamport's Bakery Algorithm: Lamport's Bakery Algorithm. For more information, please follow other related articles on the PHP Chinese website!




