 Backend Development
Backend Development
 C++
C++
 Number of paths from root to leaves with at most M consecutive nodes and value K
Number of paths from root to leaves with at most M consecutive nodes and value K
Number of paths from root to leaves with at most M consecutive nodes and value K
Introduction
Binary trees are a fascinating data structure with a wide range of applications in computer science and programming. An interesting problem is to find the count from a given tree consisting of a parent node and its children. A binary tree is composed of nodes, the root node is determined, and the root node can provide child nodes according to user needs. The K value is determined, and the movement method is selected by the M value.
Count of root to leaf paths
The graph is created using various nodes that hold values in the form of integers. This article mainly focuses on counting from the starting node or root node to the leaf node or child node.
Example
The graph is created from a binary tree with various nodes.
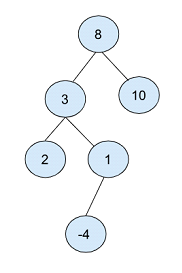
In the above binary tree, the root node is selected as "8".
Then create two nodes, one with a value of 3 and the other with a value of 10, occupying the left and right positions of the root node.
With the node with value 2 as the root, create another child node with values 2 and 1 as left and right nodes respectively.
Finally, a child node with a value of 1 creates a child node with a value of -4.
Method 1: C code to use a recursive function to compute a root-to-leaf path consisting of up to M consecutive nodes with K values
To solve this problem efficiently, we will utilize basic concepts such as tree traversal algorithm and recursion.
algorithm
Step 1: Create a structure to represent the tree node, which includes two pointers (left child node and right child node) and an integer field to store the node value.
Step 2: Design a recursive function to traverse the binary tree starting from the root, while tracking the current path length (initialized to 0), the number of consecutive occurrences (initially set to 0), and the target value K, allowing The maximum number of consecutive occurrences M.
Step 3: Call the function recursively on each left and right subtree, passing updated parameters such as incremental path length and number of consecutive occurrences (if applicable).
Step 4: For each non-empty node visited during the traversal:
a) If its value is equal to K, add one to both variables.
b) Reset the variable to zero if its value does not match K or exceeds the number of consecutive occurrences of M that have been encountered so far in the path.
Step 5: While traversing the tree, if the value of the child node is zero in both the left and right cases - we can handle it in two ways, namely
a) Check whether the variable does not exceed M.
b) If yes, increase the total number of paths that meet the condition by 1.
Example
//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
if (end == NULL || consCount > M) {
return 0;
}
//To check when the root is equal to the K value, increment by 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//If it is not equal, it will return 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // Value of node
int M = 2; // Maximum consecutive nodes
int currCount = -1; // Current count
int consCount = -1; // Consecutive count
cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
Output
The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3
in conclusion
In this article, we explore the problem of counting the number of paths from the top (i.e., leaf) to the tip or root. Such problems can be solved efficiently by using tree traversal algorithms and recursive techniques in C. The process of traversing a binary tree may seem difficult, but it becomes easy with examples.
The above is the detailed content of Number of paths from root to leaves with at most M consecutive nodes and value K. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 What is an MD5 hash value?
Feb 18, 2024 pm 08:50 PM
What is an MD5 hash value?
Feb 18, 2024 pm 08:50 PM
What is the MD5 value? In computer science, MD5 (MessageDigestAlgorithm5) is a commonly used hash function used to digest or encrypt messages. It produces a fixed-length 128-bit binary number, usually represented in 32-bit hexadecimal. The MD5 algorithm was designed by Ronald Rivest in 1991. Although the MD5 algorithm is considered no longer secure in the field of cryptography, it is still widely used in data integrity verification and file verification.
 PHP value analysis: Detailed explanation of the concept and application of values in PHP
Mar 21, 2024 pm 09:06 PM
PHP value analysis: Detailed explanation of the concept and application of values in PHP
Mar 21, 2024 pm 09:06 PM
PHP value analysis: Detailed explanation of the concept and application of value in PHP In PHP programming, value is a very basic and important concept. In this article, we will take a deep dive into the concept of values in PHP and its application in real-world programming. We will analyze in detail basic value types, variables, arrays, objects and constants, etc., and provide specific code examples to help readers better understand and use values in PHP. Basic value types In PHP, the most common basic value types include integer, floating point, string, Boolean and null. These basic
 Explore unaddressable values in Go
Mar 25, 2024 am 09:33 AM
Explore unaddressable values in Go
Mar 25, 2024 am 09:33 AM
In the Go language, some values are not addressable, that is, their memory addresses cannot be obtained. These values include constants, literals, and expressions that cannot be addressed. In this article, we will explore these non-addressable values and understand their characteristics through concrete code examples. First, let's look at some examples of constants. In the Go language, constants are not addressable because their values are determined at compile time and there is no runtime memory address for access. Here is a sample code: packagemaini
 Programming in C++, find the number of paths from one point to another in a grid
Aug 29, 2023 pm 10:25 PM
Programming in C++, find the number of paths from one point to another in a grid
Aug 29, 2023 pm 10:25 PM
In this article, we are given a problem where we need to find the total number of paths from point A to point B, where A and B are fixed points, i.e. A is the upper left corner point in the grid and B is the Lower right corner point, for example −Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20 In the given problem, we can formalize the answer and derive the result through simple observations. Method of finding the solution In this method we come up with a formula by observing that when crossing the grid from A to B we need to go right n times and down n times which means we need to find all possible path combinations, so we get
 Optional class in Java 8: How to filter possibly null values using filter() method
Aug 01, 2023 pm 05:27 PM
Optional class in Java 8: How to filter possibly null values using filter() method
Aug 01, 2023 pm 05:27 PM
Optional class in Java8: How to use the filter() method to filter possibly null values In Java8, the Optional class is a very useful tool that allows us to better handle possibly null values and avoid the occurrence of NullPointerException. The Optional class provides many methods to manipulate potential null values, one of the important methods is filter(). The function of the filter() method is that if Option
 Find the number of paths with weight W in a K-ary tree using C++
Sep 16, 2023 pm 06:09 PM
Find the number of paths with weight W in a K-ary tree using C++
Sep 16, 2023 pm 06:09 PM
In this article, we will use C++ to count the number of paths with weight W in a K-ary tree. We have been given a K-ary tree, which is a tree in which each node has K children and each edge has a weight, with the weight decreasing from 1 to K from a node to all its children. We need to count the cumulative number of paths starting from the root node that have weight W and at least one edge with weight M. So, here is an example: Input:W=4,K=3,M=2Output:6 In the given problem, we will use dp to reduce the time and space complexity. By using memoization, we can make our programs faster and adapt them to larger constraints. Method In this method we will traverse the tree and trace the usage of
 Explore the charm of Java Map and solve the problems of data processing
Feb 19, 2024 pm 07:03 PM
Explore the charm of Java Map and solve the problems of data processing
Feb 19, 2024 pm 07:03 PM
Explanation of Map Map is a data structure that allows you to store key-value pairs. The keys are unique and the values can be any type of object. The Map interface provides methods for storing and retrieving key-value pairs, and allows you to traverse the key-value pairs in the Map. Types of Map There are several different implementations of Map in Java, the most common ones are HashMap, TreeMap and LinkedHashMap. HashMap: A Map implementation based on a hash table, which has the characteristics of fast search, insertion and deletion, but it is not ordered, which means that the order of key-value pairs in the Map is arbitrarily determined. TreeMap: A Map implementation based on red-black trees, with the characteristics of fast search, insertion and deletion, and it has
 What happens when converting a value to a boolean in JavaScript?
Sep 02, 2023 am 09:21 AM
What happens when converting a value to a boolean in JavaScript?
Sep 02, 2023 am 09:21 AM
Convert to a Boolean value using the Boolean() method in JavaScript. You can try running the following code to understand how to convert [50,100] to boolean in JavaScript. Example real-time demonstration<!DOCTYPEhtml><html> <body> <p>Convert[50,100]toBoolean</p> &



