 Backend Development
Backend Development
 C++
C++
 In C++, translate the following into Chinese: Count the number of numbers between L and R that are relatively prime to P
In C++, translate the following into Chinese: Count the number of numbers between L and R that are relatively prime to P
In C++, translate the following into Chinese: Count the number of numbers between L and R that are relatively prime to P

In the world of computer programming, finding the number of numbers in a given range that is coprime to a specific number can be a common task. Relatively prime numbers, also known as relative prime numbers, are numbers that have no common factors other than 1. In this article, we will explore finding the number of numbers that are relatively prime to a specific number P between given integers L and R by using C language.
grammar
We will first outline the syntax of the methods we will use in the following code examples -
int countCoprimes(int L, int R, int P);
algorithm
The algorithm we will use to calculate the number of coprime numbers is as follows −
Initialize the variable count to 0, which is used to store the count of coprime numbers.
Iterate each number num starting from L until R.
For each num, check whether it is relatively prime with P.
If num and P are relatively prime, increase the count by 1.
Return the final value of count.
Method 1: Naive method
The first method we will discuss is the naive method. In order to verify coprimeness with P using Euclidean's algorithm, this method requires iteratively checking each number within a specified range.
The Chinese translation ofExample
is:Example
#include <iostream>
int countCoprimes(int L, int R, int P) {
int count = 0;
for (int num = L; num <= R; num++) {
int a = num;
int b = P;
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
if (a == 1)
count++;
}
return count;
}
int main() {
int L = 1; // Set the starting range value
int R = 100; // Set the ending range value
int P = 7; // Set the value of P
int result = countCoprimes(L, R, P);
std::cout << "Count of numbers between " << L << " and " << R << " coprime with " << P << ": " << result << std::endl;
return 0;
}
Output
Count of numbers between 1 and 100 coprime with 7: 86
Explanation
is:Explanation
The countCoprimes function accepts three parameters: L (starting range value), R (ending range value) and P (value of P).
Inside the countCoprimes function, we initialize a variable count to 0, which will store the count of coprime numbers.
The for loop iterates each number num from L to R.
In the loop, we initialize the variables a and b to num and P respectively.
We use the Euclidean algorithm in the while loop to find the greatest common divisor (GCD) of a and b by repeatedly exchanging and performing modular operations.
If GCD (stored in a) is equal to 1, this means that num and P are co-prime. In this case, we increment the count variable.
We finalize our count value by carefully iterating through all the numbers and returning it when complete.
Main functions thoughtfully assign appropriate values to L, R and P variables.
We then call the countCoprimes function with the provided value and store the result in the result variable.
Finally, we display the result, which is the count of numbers that are relatively prime to P between L and R.
Method 2: Prime factor decomposition
This strategy involves exploiting prime factorization of P to accurately calculate the number of coprime integers that fall between L and R.
The Chinese translation ofExample
is:Example
#include <iostream>
#include <unordered_set>
int countCoprimes(int L, int R, int P) {
std::unordered_set<int> factors;
int tempP = P;
for (int i = 2; i * i <= tempP; i++) {
while (tempP % i == 0) {
factors.insert(i);
tempP /= i;
}
}
if (tempP > 1)
factors.insert(tempP);
int count = 0;
for (int num = L; num <= R; num++) {
bool isCoprime = true;
for (int factor : factors) {
if (num % factor == 0) {
isCoprime = false;
break;
}
}
if (isCoprime)
count++;
}
return count;
}
int main() {
int L = 1; // Set the starting range value
int R = 100; // Set the ending range value
int P = 7; // Set the value of P
int result = countCoprimes(L, R, P);
std::cout << "Count of numbers between " << L << " and " << R << " coprime with " << P << ": " << result << std::endl;
return 0;
}
Output
Count of numbers between 1 and 100 coprime with 7: 86
Explanation
is:Explanation
The countCoprimes function accepts three parameters: L (starting range value), R (ending range value) and P (value of P).
We create an unordered factor set to store the prime factors of P. We initialize a temporary variable tempP to P.
We iterate from 2 to the square root of tempP. If tempP is divisible by i, we add i to the set of factors and divide tempP by i until tempP is no longer divisible by i.
If tempP is greater than 1 after the above loop, it means that it is a prime number and should be added to the factor.
We initialize the variable count to 0, which will store the count of coprime numbers.
We iterate over each number num from L to R and check if it is divisible by any factor in the set factors. If we can, we label it non-coprime.
After completing the iteration of all numbers, the resulting count will be returned as the final value. As for the main function, it initializes L, R and P with the specified values.
We then call the countCoprimes function with the provided value and store the result in the result variable.
Finally, we display the result, which is the count of numbers that are relatively prime to P between L and R.
in conclusion
Calculating coprime numbers within a specified range L-R, and satisfying a specific value P, is a good challenge for programmers - but at the code level, what is the best approach? As part of this article, we take a deep dive into two C use cases that offer real efficiencies when solving problems like this. First, by iterating over all values within the target interval and using the Euclidean algorithm to check whether the numbers match as coprime numbers; and also by using the Euler function method, which uses an optimization strategy. Regardless of which method you use, whether you can get the most out of it depends largely on contextual factors, like the numbers you choose and the intervals you specify, but choosing wisely between the two possible methods can really speed things up overall. The execution speed of the program. For coders looking to add technical savvy to their technical skills and creative problem-solving abilities, mastering coprime number counting using C through these methods may be just what they need.
The above is the detailed content of In C++, translate the following into Chinese: Count the number of numbers between L and R that are relatively prime to P. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
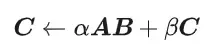 CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) is a vital part of many applications and algorithms, and is also one of the important indicators for evaluating computer hardware performance. In-depth research and optimization of the implementation of GEMM can help us better understand high-performance computing and the relationship between software and hardware systems. In computer science, effective optimization of GEMM can increase computing speed and save resources, which is crucial to improving the overall performance of a computer system. An in-depth understanding of the working principle and optimization method of GEMM will help us better utilize the potential of modern computing hardware and provide more efficient solutions for various complex computing tasks. By optimizing the performance of GEMM
 How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
WORD is a powerful word processor. We can use word to edit various texts. In Excel tables, we have mastered the calculation methods of addition, subtraction and multipliers. So if we need to calculate the addition of numerical values in Word tables, How to subtract the multiplier? Can I only use a calculator to calculate it? The answer is of course no, WORD can also do it. Today I will teach you how to use formulas to calculate basic operations such as addition, subtraction, multiplication and division in tables in Word documents. Let's learn together. So, today let me demonstrate in detail how to calculate addition, subtraction, multiplication and division in a WORD document? Step 1: Open a WORD, click [Table] under [Insert] on the toolbar, and insert a table in the drop-down menu.
 How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to use Python's count() function to calculate the number of an element in a list requires specific code examples. As a powerful and easy-to-learn programming language, Python provides many built-in functions to handle different data structures. One of them is the count() function, which can be used to count the number of elements in a list. In this article, we will explain how to use the count() function in detail and provide specific code examples. The count() function is a built-in function of Python, used to calculate a certain
 Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Given two strings str_1 and str_2. The goal is to count the number of occurrences of substring str2 in string str1 using a recursive procedure. A recursive function is a function that calls itself within its definition. If str1 is "Iknowthatyouknowthatiknow" and str2 is "know" the number of occurrences is -3. Let us understand through examples. For example, input str1="TPisTPareTPamTP", str2="TP"; output Countofoccurrencesofasubstringrecursi
 Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Introduction The Java program for calculating the area of a triangle using determinants is a concise and efficient program that can calculate the area of a triangle given the coordinates of three vertices. This program is useful for anyone learning or working with geometry, as it demonstrates how to use basic arithmetic and algebraic calculations in Java, as well as how to use the Scanner class to read user input. The program prompts the user for the coordinates of three points of the triangle, which are then read in and used to calculate the determinant of the coordinate matrix. Use the absolute value of the determinant to ensure the area is always positive, then use a formula to calculate the area of the triangle and display it to the user. The program can be easily modified to accept input in different formats or to perform additional calculations, making it a versatile tool for geometric calculations. ranks of determinants
 How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
In C#, there is a Math class library, which contains many mathematical functions. These include the function Math.Pow, which calculates powers, which can help us calculate the power of a specified number. The usage of the Math.Pow function is very simple, you only need to specify the base and exponent. The syntax is as follows: Math.Pow(base,exponent); where base represents the base and exponent represents the exponent. This function returns a double type result, that is, the power calculation result. Let's
 Java program example to calculate total score and percentage
Sep 11, 2023 pm 06:01 PM
Java program example to calculate total score and percentage
Sep 11, 2023 pm 06:01 PM
We will demonstrate how to calculate total scores and percentages using a Java program. Total score refers to the sum of all available scores, while the term percentage refers to the calculated score divided by the total score and multiplied by the resulting number 100. percentage_of_marks=(obtained_marks/total_marks)×100 Example 1 This is a Java program that demonstrates how to calculate total scores and percentages. //JavaProgramtodemonstratehowisTotalmarksandPercentagescalculatedimportjava.io.*;publicclassTotalMarks_
 PHP date processing tips: How to calculate the month difference between dates using PHP?
Mar 20, 2024 am 11:24 AM
PHP date processing tips: How to calculate the month difference between dates using PHP?
Mar 20, 2024 am 11:24 AM
PHP date processing tips: How to calculate the month difference between dates using PHP? Date processing is a very common requirement in web development, especially in business logic that needs to be related to time. In PHP, calculating the month difference between dates can be achieved through some methods. This article will introduce how to use PHP to calculate the month difference between two dates and provide specific code examples. Method 1: Use the DateTime class. PHP's DateTime class provides a wealth of date processing methods, including calculating dates.



