Find the number of solutions to a modular equation using C++

In this article we will explain what solutions to modular equations are and we will also write a program to find multiple solutions to modular equations. Here is the basic example -
Input : X = 30 Y = 2 Output : 4, 7, 14, 28 Explanation : 30 mod 4 = 2 (equals Y), 30 mod 7 = 2 (equals Y), 30 mod 14 = 2 (equals Y), 30 mod 28 = 2 (equals Y) Input : X = 30 Y = 2 Output : 4, 7, 14, 28 Explanation : 30 mod 4 = 2 (equals Y), 30 mod 7 = 2 (equals Y), 30 mod 14 = 2 (equals Y), 30 mod 28 = 2 (equals Y)
As we have seen in the above example, every integer is a solution that gives a remainder Y after dividing X. In this example, dividing 30 by 4, 7, 14, and 28 gives a remainder of 2, which is equal to Y. We will solve the modular equation this way.
Method to solve
We can apply a simple method of dividing X by every integer starting from 1 and check if it gives remainder Y, or we can put X - Y) is divided by every integer, and an integer that divides (X - Y) but not X is the solution. Let's write a C program to find different solutions to a modular equation.
Example
#include <bits/stdc++.h>
using namespace std;
int numberofdivisor(int X, int Y){
int N = (X - Y);
int noOfDivisors = 1;
for (int i = 1; i <= N/2; i++) {
// if N is divisible by i
if ((N % i) == 0) {
// count if integer is greater than Y
if (i > Y)
noOfDivisors++;
}
}
return noOfDivisors;
}
void numberofsolutions(int X, int Y){
int noOfSolutions;
if (X == Y)
noOfSolutions = -1;
if (X < Y)
noOfSolutions = 0;
if (X > Y)
noOfSolutions = numberofdivisor(X, Y);
if (noOfSolutions == -1) {
cout << "X can take Infinitely many values"
" greater than " << X << "\n";
}
else {
cout << "Number of solution = " << noOfSolutions;
}
}
// main function
int main(){
int X,Y;
cin >> X;
cin >> Y;
numberofsolutions(X, Y);
return 0;
}Output
When we write 0 as input, the program gives the following output-
X can take Infinitely many values greater than 0
When we enter other numbers , the above program will show an output like this (here we have provided 5 as input) -
Number of solution = 2
Explanation of the above code
Now we explain each function so that you can understand it easily program.
main() function
In the main function, we take the values of X and Y as input and find the number of possible solutions by calling the numberofsolutions() function.
Numberofsolutions() function
This function checks whether X and Y satisfy the condition that X should be greater than Y, because we cannot find a remainder greater than the dividend. This function calls another function numberofdivisor() and gets the number of divisors of X, resulting in the remainder Y.
Numberofdivisor() Function
This function finds the number of divisors of X - Y by running a loop from 1 to (X - Y)/2 and checking whether each integer is divisible and The integer should not exactly divide X.
Conclusion
The solution to a modular equation is an integer that divides X and gets the remainder Y; we know this from various examples. The equation can have some solutions, so we find these solutions by applying simple methods.
We can write a C program to compute the solution to the modular equation. We can write the same program in other languages like C, Java, Python or any other programming language. I hope you found this article helpful in understanding the concept of how to find multiple solutions to modular equations.
The above is the detailed content of Find the number of solutions to a modular equation using C++. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1387
1387
 52
52
 C language data structure: data representation and operation of trees and graphs
Apr 04, 2025 am 11:18 AM
C language data structure: data representation and operation of trees and graphs
Apr 04, 2025 am 11:18 AM
C language data structure: The data representation of the tree and graph is a hierarchical data structure consisting of nodes. Each node contains a data element and a pointer to its child nodes. The binary tree is a special type of tree. Each node has at most two child nodes. The data represents structTreeNode{intdata;structTreeNode*left;structTreeNode*right;}; Operation creates a tree traversal tree (predecision, in-order, and later order) search tree insertion node deletes node graph is a collection of data structures, where elements are vertices, and they can be connected together through edges with right or unrighted data representing neighbors.
 The truth behind the C language file operation problem
Apr 04, 2025 am 11:24 AM
The truth behind the C language file operation problem
Apr 04, 2025 am 11:24 AM
The truth about file operation problems: file opening failed: insufficient permissions, wrong paths, and file occupied. Data writing failed: the buffer is full, the file is not writable, and the disk space is insufficient. Other FAQs: slow file traversal, incorrect text file encoding, and binary file reading errors.
 C language multithreaded programming: a beginner's guide and troubleshooting
Apr 04, 2025 am 10:15 AM
C language multithreaded programming: a beginner's guide and troubleshooting
Apr 04, 2025 am 10:15 AM
C language multithreading programming guide: Creating threads: Use the pthread_create() function to specify thread ID, properties, and thread functions. Thread synchronization: Prevent data competition through mutexes, semaphores, and conditional variables. Practical case: Use multi-threading to calculate the Fibonacci number, assign tasks to multiple threads and synchronize the results. Troubleshooting: Solve problems such as program crashes, thread stop responses, and performance bottlenecks.
 How to output a countdown in C language
Apr 04, 2025 am 08:54 AM
How to output a countdown in C language
Apr 04, 2025 am 08:54 AM
How to output a countdown in C? Answer: Use loop statements. Steps: 1. Define the variable n and store the countdown number to output; 2. Use the while loop to continuously print n until n is less than 1; 3. In the loop body, print out the value of n; 4. At the end of the loop, subtract n by 1 to output the next smaller reciprocal.
 CS-Week 3
Apr 04, 2025 am 06:06 AM
CS-Week 3
Apr 04, 2025 am 06:06 AM
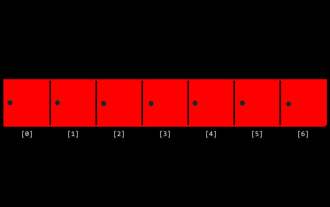
Algorithms are the set of instructions to solve problems, and their execution speed and memory usage vary. In programming, many algorithms are based on data search and sorting. This article will introduce several data retrieval and sorting algorithms. Linear search assumes that there is an array [20,500,10,5,100,1,50] and needs to find the number 50. The linear search algorithm checks each element in the array one by one until the target value is found or the complete array is traversed. The algorithm flowchart is as follows: The pseudo-code for linear search is as follows: Check each element: If the target value is found: Return true Return false C language implementation: #include#includeintmain(void){i
 C language data structure: the key role of data structures in artificial intelligence
Apr 04, 2025 am 10:45 AM
C language data structure: the key role of data structures in artificial intelligence
Apr 04, 2025 am 10:45 AM
C Language Data Structure: Overview of the Key Role of Data Structure in Artificial Intelligence In the field of artificial intelligence, data structures are crucial to processing large amounts of data. Data structures provide an effective way to organize and manage data, optimize algorithms and improve program efficiency. Common data structures Commonly used data structures in C language include: arrays: a set of consecutively stored data items with the same type. Structure: A data type that organizes different types of data together and gives them a name. Linked List: A linear data structure in which data items are connected together by pointers. Stack: Data structure that follows the last-in first-out (LIFO) principle. Queue: Data structure that follows the first-in first-out (FIFO) principle. Practical case: Adjacent table in graph theory is artificial intelligence
 Troubleshooting tips for processing files in C language
Apr 04, 2025 am 11:15 AM
Troubleshooting tips for processing files in C language
Apr 04, 2025 am 11:15 AM
Troubleshooting Tips for C language processing files When processing files in C language, you may encounter various problems. The following are common problems and corresponding solutions: Problem 1: Cannot open the file code: FILE*fp=fopen("myfile.txt","r");if(fp==NULL){//File opening failed} Reason: File path error File does not exist without file read permission Solution: Check the file path to ensure that the file has check file permission problem 2: File reading failed code: charbuffer[100];size_tread_bytes=fread(buffer,1,siz
 The concept of c language functions and their definition format
Apr 03, 2025 pm 11:33 PM
The concept of c language functions and their definition format
Apr 03, 2025 pm 11:33 PM
C language functions are reusable code blocks, receive parameters for processing, and return results. It is similar to the Swiss Army Knife, powerful and requires careful use. Functions include elements such as defining formats, parameters, return values, and function bodies. Advanced usage includes function pointers, recursive functions, and callback functions. Common errors are type mismatch and forgetting to declare prototypes. Debugging skills include printing variables and using a debugger. Performance optimization uses inline functions. Function design should follow the principle of single responsibility. Proficiency in C language functions can significantly improve programming efficiency and code quality.




