 Backend Development
Backend Development
 C++
C++
 C++ program to calculate the hyperbolic tangent of a given value in radians
C++ program to calculate the hyperbolic tangent of a given value in radians
C++ program to calculate the hyperbolic tangent of a given value in radians

Like regular trigonometric functions, hyperbolic functions are defined using hyperbolas instead of circles. In hyperbolic geometry, hyperbolic functions are used to calculate angles and distances. Additionally, they can be found in the answers to a large number of linear differential equations, cubic equations, etc. For a given angle $\theta$. The hyperbolic tangent function tanh$(\theta)$ is as follows -
$$\mathrm{tanh(x)\:=\:\frac{sinh(x)}{cosh(x)}\:=\:\frac{e^{x}-e^{-x }}{e^{x} e^{-x}}\:=\:\frac{e^{2x}-1}{e^{2x} 1}}$$
In this article we will discuss techniques for obtaining the value of tanh$(\theta)$ in C when the angle is given in radians.
tanh() function
This tanh$(\theta)$ requires the tanh() function in the C cmath library to run. This function takes an angle in radians as input and outputs a hyperbolic cosine value. Simple syntax is used below.
grammar
#include < cmath > tanh( <angle in radian> )
algorithm
- Take angle x (expressed in radians) as input.
- Use tanh(x) to calculate tanh (x).
- Return results.
Example
#include <iostream>
#include <cmath>
using namespace std;
float solve( float x ) {
float answer;
answer = tanh( x );
return answer;
}
int main()
{
cout << "The value of tanh( pi/2 ) is: " << solve( 3.14159 / 2 ) << endl;
cout << "The value of tanh( pi ) is: " << solve( 3.14159 ) << endl;
cout << "The value of tanh with an angle of 90 degrees is: " << solve( 90 * 3.14159 / 180 ) << endl;
cout << "The value of tanh with an angle of 45 degrees is: " << solve( 45 * 3.14159 / 180 ) << endl;
}
Output
The value of tanh( pi/2 ) is: 0.917152 The value of tanh( pi ) is: 0.996272 The value of tanh with an angle of 90 degrees is: 0.917152 The value of tanh with an angle of 45 degrees is: 0.655794
The first two input numbers in this example are in radians, while the last two are degrees that have been converted to radians using the following formula -
$$\mathrm{\theta_{rad}\:=\:\theta_{deg}\:\times\:\frac{\pi}{180}}$$
in conclusion
To calculate the hyperbolic tangent of a given angle in radians in C, use the tanh() function. Although the cmath header file is part of the standard library, it needs to be included in our C code to use this function. The tanh() function returns the value HUGE VAL and sets the error code to ERANGE if the result is too large (can be positive or negative, depending on the value of x). Although the C90 version of C had a double return type, later versions of C overloaded methods for float and long double in addition to better generic (template) usage for integral types. Several parameters of this function are used in the article, whether in radians or degrees; however, for degrees, the value is converted to radians using the formula given above.
The above is the detailed content of C++ program to calculate the hyperbolic tangent of a given value in radians. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
WORD is a powerful word processor. We can use word to edit various texts. In Excel tables, we have mastered the calculation methods of addition, subtraction and multipliers. So if we need to calculate the addition of numerical values in Word tables, How to subtract the multiplier? Can I only use a calculator to calculate it? The answer is of course no, WORD can also do it. Today I will teach you how to use formulas to calculate basic operations such as addition, subtraction, multiplication and division in tables in Word documents. Let's learn together. So, today let me demonstrate in detail how to calculate addition, subtraction, multiplication and division in a WORD document? Step 1: Open a WORD, click [Table] under [Insert] on the toolbar, and insert a table in the drop-down menu.
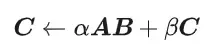 CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) is a vital part of many applications and algorithms, and is also one of the important indicators for evaluating computer hardware performance. In-depth research and optimization of the implementation of GEMM can help us better understand high-performance computing and the relationship between software and hardware systems. In computer science, effective optimization of GEMM can increase computing speed and save resources, which is crucial to improving the overall performance of a computer system. An in-depth understanding of the working principle and optimization method of GEMM will help us better utilize the potential of modern computing hardware and provide more efficient solutions for various complex computing tasks. By optimizing the performance of GEMM
 How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to use Python's count() function to calculate the number of an element in a list requires specific code examples. As a powerful and easy-to-learn programming language, Python provides many built-in functions to handle different data structures. One of them is the count() function, which can be used to count the number of elements in a list. In this article, we will explain how to use the count() function in detail and provide specific code examples. The count() function is a built-in function of Python, used to calculate a certain
 How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
In C#, there is a Math class library, which contains many mathematical functions. These include the function Math.Pow, which calculates powers, which can help us calculate the power of a specified number. The usage of the Math.Pow function is very simple, you only need to specify the base and exponent. The syntax is as follows: Math.Pow(base,exponent); where base represents the base and exponent represents the exponent. This function returns a double type result, that is, the power calculation result. Let's
 Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Given two strings str_1 and str_2. The goal is to count the number of occurrences of substring str2 in string str1 using a recursive procedure. A recursive function is a function that calls itself within its definition. If str1 is "Iknowthatyouknowthatiknow" and str2 is "know" the number of occurrences is -3. Let us understand through examples. For example, input str1="TPisTPareTPamTP", str2="TP"; output Countofoccurrencesofasubstringrecursi
 C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
Hyperbolic functions are defined using hyperbolas instead of circles and are equivalent to ordinary trigonometric functions. It returns the ratio parameter in the hyperbolic sine function from the supplied angle in radians. But do the opposite, or in other words. If we want to calculate an angle from a hyperbolic sine, we need an inverse hyperbolic trigonometric operation like the hyperbolic inverse sine operation. This course will demonstrate how to use the hyperbolic inverse sine (asinh) function in C++ to calculate angles using the hyperbolic sine value in radians. The hyperbolic arcsine operation follows the following formula -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Where\:In\:is\:natural logarithm\:(log_e\:k)
 C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
A map is a special type of container in C++ in which each element is a pair of two values, namely a key value and a map value. The key value is used to index each item, and the mapped value is the value associated with the key. Regardless of whether the mapped value is unique, the key is always unique. To print map elements in C++ we have to use iterator. An element in a set of items is indicated by an iterator object. Iterators are primarily used with arrays and other types of containers (such as vectors), and they have a specific set of operations that can be used to identify specific elements within a specific range. Iterators can be incremented or decremented to reference different elements present in a range or container. The iterator points to the memory location of a specific element in the range. Printing a map in C++ using iterators First, let's look at how to define
 C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
The rename function changes a file or directory from its old name to its new name. This operation is similar to the move operation. So we can also use this rename function to move files. This function exists in the stdio.h library header file. The syntax of the rename function is as follows: intrename(constchar*oldname,constchar*newname); The function of the rename() function accepts two parameters. One is oldname and the other is newname. Both parameters are pointers to constant characters that define the old and new names of the file. Returns zero if the file was renamed successfully; otherwise, returns a nonzero integer. During a rename operation





