The sum of all pairs of shortest paths in the tree

In trees, the term "sum of the shortest paths of all pairs of nodes" refers to the calculation of the sum of the individual shortest paths of all pairs of nodes. An effective method is to use the dual DFS (depth first search) algorithm. The distance between the selected node and every other node is determined during the first DFS pass. The tree is traversed again during the second DFS pass, considering each node as a potential LCA (lowest common ancestor) and calculating the sum of distances between pairs of descendant nodes of the selected LCA. Using this method you can calculate the sum of the shortest paths for all pairs of nodes in the tree and ensure an ideal solution
usage instructions
Double DFS (depth first search) method
Dynamic programming method
Double DFS (depth first search) method
For the sum of all pairs of shortest paths in the tree, we use a dual DFS (depth-first search) method, which involves two DFS passes. First, we calculate the distance from any node to all other nodes. Then, during the second DFS traversal, we navigate the tree while considering each node as a potential LCA. We calculate and sum the distances between pairs of nodes that are descendants of the selected LCA while traversing. By repeating this process for all nodes, we obtain the sum of all pairs of shortest paths. This strategy is very compelling for this problem because it effectively computes the sum of distances between all sets of nodes in the tree.
algorithm
Any node in the tree can be used as the starting node
To determine the distance from the selected starting node to all other nodes, perform a depth-first search (DFS) starting from that node. These distances should be saved in an array or data structure.
Next, run a second depth-first search (DFS) on the tree, considering each node as its possible nearest common ancestor (LCA)
During the second DFS traversal of the tree, calculate the distance between pairs of nodes that are descendants of the selected LCA. For each LCA, these distances are added together.
Repeat this process for each node in the tree
The sum of all matches in the most limited way in the tree is represented by the sum of all calculated distances in step 4.
Example
is:Example
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
|
Output
1 |
|
Dynamic programming method:
We first select any node as the root node, and convert the tree into a rooted tree in the dynamic programming method, which is used to calculate the sum of the shortest paths between all nodes in the tree. We use dynamic programming to calculate the split between each node and the root node and store the results in an array. Then, for each node, we add the (computed) separations of its children from the root node to determine the overall separation of all other nodes. In this way, we can quickly calculate the total number of shortest paths between all nodes. As an efficient way to solve this problem, the time complexity of this algorithm is O(N), where N is the number of nodes in the tree.
algorithm
Take any node in the tree as the root and root the tree (for example, using a depth search of the root node) to create a rooted tree.
Dynamic programming can be used to determine the distance of each node from the root. These distances should be stored in an array or data structure.
Calculate the sum of the distances from each node to all other nodes in the tree:
The sum of all pairs of shortest paths in the tree is the final result.
a. Traverse the child nodes of the current node.
b. To consider the path through the current node, add the number of nodes in the subtree for each subtree and the distance to the root previously calculated for each subtree.
c. For each child node of the active node, add these amounts
d. Add the current node's total to the final result.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
|
Output
1 |
|
in conclusion
The sum of all pairs of shortest paths in the tree can be calculated using the Double DFS (Depth First Search) method or dynamic programming. The Double DFS method consists of two passes, first calculating the distance from the selected node to all other nodes, and then traversing the tree again while treating each node as a potential lowest common ancestor (LCA) to sum the distances between Descendant node pairs. Dynamic programming methods require recursively using DFS to build the root of the tree and calculate the distance from the root to every other node. The result of both methods is the same and consists of the sum of all pairwise shortest paths in the tree. The decision between two algorithms may be based on specific implementation preferences or tree structures, but both algorithms provide efficient solutions.
The above is the detailed content of The sum of all pairs of shortest paths in the tree. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 1207
1207
 24
24
 The sum of all pairs of shortest paths in the tree
Aug 28, 2023 pm 03:17 PM
The sum of all pairs of shortest paths in the tree
Aug 28, 2023 pm 03:17 PM
In trees, the term "sum of the shortest paths of all pairs of nodes" refers to the calculation of the sum of the individual shortest paths of all pairs of nodes. An effective method is to use the dual DFS (depth first search) algorithm. The distance between the selected node and every other node is determined during the first DFS pass. The tree is traversed again during the second DFS pass, considering each node as a potential LCA (lowest common ancestor) and calculating the sum of distances between pairs of descendant nodes of the selected LCA. Using this method you can calculate the sum of the shortest paths for all pairs of nodes in the tree and ensure an ideal solution Methods used Dual DFS (Depth First Search) method Dynamic programming method Dual DFS (Depth First Search) method for the tree All pairs of shortest paths
 How to implement the shortest path algorithm using java
Sep 19, 2023 am 08:18 AM
How to implement the shortest path algorithm using java
Sep 19, 2023 am 08:18 AM
Overview of how to use Java to implement the shortest path algorithm: The shortest path algorithm is an important application in graph theory and is widely used in network routing, map navigation and other fields. In this article, we will learn how to implement the shortest path algorithm using Java and provide concrete code examples. Algorithm idea: There are many ways to implement the shortest path algorithm, among which the two most famous algorithms are Dijkstra algorithm and A* algorithm. Here we will focus on the implementation of Dijkstra's algorithm. The basis of Dijkstra's algorithm
 In-depth exploration of the application and implementation methods of non-linear data structures of trees and graphs in Java
Dec 26, 2023 am 10:22 AM
In-depth exploration of the application and implementation methods of non-linear data structures of trees and graphs in Java
Dec 26, 2023 am 10:22 AM
Understanding Trees and Graphs in Java: Exploring Applications and Implementations of Nonlinear Data Structures Introduction In computer science, data structures are the way data is stored, organized, and managed in computers. Data structures can be divided into linear data structures and non-linear data structures. Trees and graphs are the two most commonly used types of nonlinear data structures. This article will focus on the concepts, applications and implementation of trees and graphs in Java, and give specific code examples. The Concept and Application of Tree A tree is an abstract data type, a collection of nodes and edges. Each node of the tree contains a number
 The wonderful use of recursion in C++ data structures: implementation of stacks and trees
May 04, 2024 pm 01:54 PM
The wonderful use of recursion in C++ data structures: implementation of stacks and trees
May 04, 2024 pm 01:54 PM
Application of recursion in C++ data structures: Stack: The stack is implemented recursively through the last-in-first-out (LIFO) structure. Tree: Tree is implemented recursively through a hierarchical structure, supporting operations such as insertion and depth calculation. Recursion provides a concise and efficient solution for processing nested structures, making the implementation of data structures more intuitive and easier to maintain.
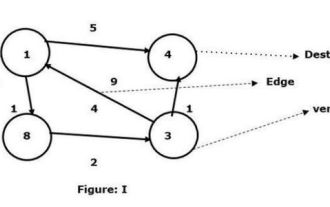 Find the shortest path between any two nodes using the Floyd-Warshal algorithm
Sep 20, 2023 pm 02:21 PM
Find the shortest path between any two nodes using the Floyd-Warshal algorithm
Sep 20, 2023 pm 02:21 PM
C++ has a macro, which is defined as a piece of code or an expected value, and it will be reused whenever the user needs it. The Floyd-Walshall algorithm is the process of finding the shortest path between all pairs of vertices in a given weighted graph. The algorithm follows a dynamic programming approach to find the minimum weight graph. Let us understand the meaning of Floyd-Walshall algorithm through a diagram - take vertex 1 as the source and vertex 4 as the destination and find the shortest path between them. We have seen that there are two paths that can be connected to the target vertex 4. 1->4 – the edge has a weight of 51->8->3->4 – the edge weight (1+2+1) is 4. In the given graph I, we see the smallest edge connecting two vertices. So here the vertex
 PHP algorithm design ideas: How to achieve an efficient solution to the shortest path problem of graphs?
Sep 19, 2023 pm 03:43 PM
PHP algorithm design ideas: How to achieve an efficient solution to the shortest path problem of graphs?
Sep 19, 2023 pm 03:43 PM
PHP algorithm design ideas: How to achieve an efficient solution to the shortest path problem of graphs? In actual development, we often need to solve the shortest path problem, such as in map navigation, network routing, logistics distribution and other fields. The shortest path algorithm for graphs is the key to solving this type of problem. A graph consists of a set of vertices and a set of edges. Vertices represent nodes, and edges represent relationships between nodes. The shortest path problem is to find the shortest path connecting two nodes. In PHP, we can use a variety of algorithms to solve the shortest path problem, the most famous of which is
 Use C++ to delete all nodes that are not on any path and the path sum is less than k
Sep 04, 2023 am 10:17 AM
Use C++ to delete all nodes that are not on any path and the path sum is less than k
Sep 04, 2023 am 10:17 AM
In this problem, we have a binary tree whose path from root node to leaf node is fully defined. The sum of all nodes from the root node to the leaf nodes must be greater than or equal to k. So we need to delete all nodes in the path whose sum is less than k. The important thing to remember here is that a node may be part of many paths, so only if the sum of all paths left is 10+20+5, which is 25, which is less than 150, we need to prune it and remove 5 . After that, let's evaluate 10->30->40. It's less than 150, so delete 40. Now we see another path 10->20->35->50 and the sum 115 is less than 150, so
 C++ program to remove nodes that do not satisfy path and are greater than or equal to k
Sep 14, 2023 am 11:25 AM
C++ program to remove nodes that do not satisfy path and are greater than or equal to k
Sep 14, 2023 am 11:25 AM
In this problem, we have a binary tree whose path from root node to leaf node is fully defined. The sum of all nodes from the root node to the leaf nodes must be greater than or equal to the constant value k. Therefore, we need to delete all nodes in those paths whose sum is less than k, so that the remaining paths in the tree will be greater than k. The important thing to remember here is that a node may be part of many paths, so only if the sum of all paths leading to that node, left, sums to 10+20+5, which is 25, less than 150, we need to Trim and remove 5. After that, let's evaluate 10->30->40. It is less than 150, so 40 is deleted. Now we see another path 10->20-




