 Backend Development
Backend Development
 C++
C++
 Find the permutation that leads to the worst case scenario of merge sort in C
Find the permutation that leads to the worst case scenario of merge sort in C
Find the permutation that leads to the worst case scenario of merge sort in C

Concept
For a given set of elements, determine which arrangement will result in the worst case scenario of merge sort?
We know that asymptotically, merge sort always takes O(n log n) time, but in practice, situations that require more comparisons usually take more time. Now we basically need to determine an arrangement of input elements that maximizes the number of comparisons when implementing a typical merge sort algorithm.
Example
Consider the following set of elements as a sorted array 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
The input array that results in the worst case scenario for merge sort is 11 19 15 23 13 21 17 25 12 20 16 24 14 22 18 26
Method
We study how to construct the worst case scenario for merge sort Input collection?
Now we try to build the array in a bottom-up manner
Now let the sorted array be {11, 12, 13, 14, 15, 16, 17, 18}.
To construct the worst-case scenario for merge sort, the merge operation resulting in the above sorted array should result in the most comparisons. Therefore, the left subarray and right subarray participating in the merge operation should alternately store the elements of the sorted array. The left subarray should be {11, 13, 15, 17}, and the right subarray should be {12, 14, 16, 18 }. This way, each element of the array will be compared at least once, resulting in a maximum number of comparisons. Now we implement the same logic for the left sub-array and the right sub-array as well. For the array {11, 13, 15, 17}, the worst case occurs when its left subarray is {11, 15} and its right subarray is {13, 17}. For the array {12, 14, 16, 18}, The worst case occurs at {12, 14} and {16, 18}.
Complete algorithm
GenerateWorstCase(arr[])
Now we create two auxiliary arrays left and right, and Store alternating array elements in them.
We call GenerateWorstCase - GenerateWorstCase (left) on the left subarray
We call GenerateWorstCase on the right subarray - GenerateWorstCase (right)
Now we copy all the elements of the left and right subarrays back to the original array.
Example
Demonstration
// C program to generate Worst Case of Merge Sort
#include <stdlib.h>
#include <stdio.h>
// Indicates function to print an array
void printArray(int A1[], int size1){
for (int i = 0; i < size1; i++)
printf("%d ", A1[i]);
printf("</p><p>");
}
// Indicates function to join left and right subarray
int join(int arr1[], int left1[], int right1[],
int l1, int m1, int r1){
int i; // So used in second loop
for (i = 0; i <= m1 - l1; i++)
arr1[i] = left1[i];
for (int j = 0; j < r1 - m1; j++)
arr1[i + j] = right1[j];
}
// Indicates function to store alternate elemets in left
// and right subarray
int split(int arr1[], int left1[], int right1[],
int l1, int m1, int r1){
for (int i = 0; i <= m1 - l1; i++)
left1[i] = arr1[i * 2];
for (int i = 0; i < r1 - m1; i++)
right1[i] = arr1[i * 2 + 1];
}
// Indicates function to generate Worst Case of Merge Sort
int generateWorstCase(int arr1[], int l1, int r1){
if (l1 < r1){
int m1 = l1 + (r1 - l1) / 2;
// creating two auxillary arrays
int left1[m1 - l1 + 1];
int right1[r1 - m1];
// Storing alternate array elements in left
// and right subarray
split(arr1, left1, right1, l1, m1, r1);
// Recursing first and second halves
generateWorstCase(left1, l1, m1);
generateWorstCase(right1, m1 + 1, r1);
// joining left and right subarray
join(arr1, left1, right1, l1, m1, r1);
}
}
// Driver code
int main(){
// Initializes sorted array
int arr1[] = { 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26 };
int n1 = sizeof(arr1) / sizeof(arr1[0]);
printf("Sorted array is </p><p>");
printArray(arr1, n1);
// generating worst Case of Merge Sort
generateWorstCase(arr1, 0, n1 - 1);
printf("</p><p>Input array that will result in " "worst case of merge sort is </p><p>");
printArray(arr1, n1);
return 0;
}Output
Sorted array is 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Input array that will result in worst case of merge sort is 11 19 15 23 13 21 17 25 12 20 16 24 14 22 18 26
The above is the detailed content of Find the permutation that leads to the worst case scenario of merge sort in C. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to check traffic on Apple mobile phone
May 09, 2024 pm 06:00 PM
How to check traffic on Apple mobile phone
May 09, 2024 pm 06:00 PM
How to check data usage on Apple 1. The specific steps to check data usage on Apple mobile phone are as follows: Open the settings of the phone. Click the Cellular button. Scroll down on the cellular network page to see the specific data usage of each application. Click Apply to also set allowed networks. 2. Turn on the phone, find the settings option on the phone desktop, and click to enter. In the settings interface, find "Cellular Network" in the taskbar below and click to enter. In the cellular network interface, find the "Usage" option on the page and click to enter. 3. Another way is to check the traffic by yourself through the mobile phone, but the mobile phone can only see the total usage and will not display the remaining traffic: turn on the iPhone, find the "Settings" option and open it. Select "Bee"
 How to disable snapshot layout in Windows 11_ Tips for not using snapshot layout in win11
May 08, 2024 pm 06:46 PM
How to disable snapshot layout in Windows 11_ Tips for not using snapshot layout in win11
May 08, 2024 pm 06:46 PM
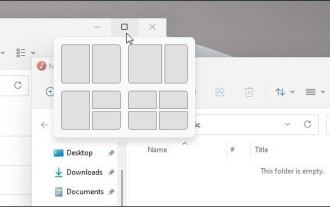
Win11 system announced the new [Snapshot Layout], which provides users with various window layout options through the [Maximize] button, so that users can choose from multiple layout templates to display two, three or four on the screen. open applications. This is an improvement over dragging multiple windows to the sides of the screen and then adjusting everything manually. [SnapGroups] will save the collection of apps the user is using and their layout, allowing the user to easily return to that setting when they have to stop and deal with other things. If someone is using a monitor that the user must unplug, when re-docking, the previously used snapshot layout will also be restored. To use snapshot layout, we can use the keyboard shortcut WindowsKey+Z to start
 How to sort the list page alphabetically in vscode How to sort the list page alphabetically in vscode
May 09, 2024 am 09:40 AM
How to sort the list page alphabetically in vscode How to sort the list page alphabetically in vscode
May 09, 2024 am 09:40 AM
1. First, after opening the vscode interface, click the settings icon button in the lower left corner of the page 2. Then, click the Settings option in the drop-down page column 3. Then, find the Explorer option in the jumped window 4. Finally, on the right side of the page Click the OpenEditorsnaming option, select the alphabetical button from the drop-down page and save the settings to complete the alphabetical sorting
 The operation process of creating bottle type text layout effect with AI
May 06, 2024 pm 02:28 PM
The operation process of creating bottle type text layout effect with AI
May 06, 2024 pm 02:28 PM
1. Open the material picture of a bottle in AI and type the text content that needs to be produced on the side. 2. Cancel the fill color of the bottle and only stroke it to form a hollow closed path. 3. Adjust the font size, font and line spacing of the text, and arrange the bottle layers to the top. 4. Select the text and the bottle at the same time, click Object-Envelope Distortion-Create with top-level object, and you will get a bottle-shaped text group. 5. Double-click the text to enter the isolation mode, and you can modify the text content and change the color. After the modification, the bottle shape will not be affected when exiting isolation mode. The final effect is as follows:
 How to set ring text in ai - specific method of setting ring text in ai
May 06, 2024 pm 05:58 PM
How to set ring text in ai - specific method of setting ring text in ai
May 06, 2024 pm 05:58 PM
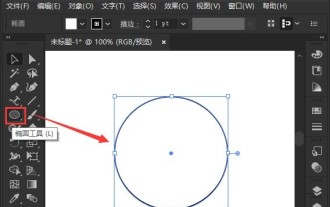
1. First, after opening the interface, click the Ellipse tool to draw a perfect circle 2. Click the Path Text tool button on the left and enter text along the circular frame 3. Select the letter with the mouse, open the character panel, and set the font size to 20.7 pt4. Select the circle, click 3D options in the effect menu, and select the rotation button 5. In the opened 3D rotation option settings, set the position option to custom rotation effect, modify the parameters and click OK to save 6. Finally, it is a ring Just add a red fill effect to the text
 How to use matplotlib to generate charts in python
May 05, 2024 pm 07:54 PM
How to use matplotlib to generate charts in python
May 05, 2024 pm 07:54 PM
To use Matplotlib to generate charts in Python, follow these steps: Install the Matplotlib library. Import Matplotlib and use the plt.plot() function to generate the plot. Customize charts, set titles, labels, grids, colors and markers. Use the plt.savefig() function to save the chart to a file.
 Can I plug in a wireless network card when assembling a computer?
May 08, 2024 am 09:13 AM
Can I plug in a wireless network card when assembling a computer?
May 08, 2024 am 09:13 AM
Can I plug in a wireless network card when assembling a computer? First of all, the wireless network card you are talking about here should be a 2G/3G/4G wireless network card, that is, a wireless network card, right? My answer is yes. However, you also need an AP that supports USB wireless network cards, such as: (only for Jiuli use, not a recommended product) Can I use a wireless network card to access the Internet by assembling a desktop computer? Network cards are essential for modern computers. Without a network card, you cannot access the Internet, whether it is an onboard network card, an independent network card, or a wireless network card. When assembling a computer, a separate network card is generally not installed, because the current motherboards have integrated network cards, so there is no need to buy another one. However, the computers assembled now cannot use wireless Internet access like notebooks, because there is no wireless network card installed. Players can According to your own needs
 How to use merge in java
May 09, 2024 am 06:03 AM
How to use merge in java
May 09, 2024 am 06:03 AM
The merge() method in Java Collections merges two sorted ordered collections to generate a new sorted collection, maintaining the original order. Syntax: public static <T> List<T> merge(SortedMap<T, Double> a, SortedMap<T, Double> b). It accepts two sorted collections and returns a new collection containing all elements in sorted order. Note: The values of duplicate keys will be merged according to the merge function, and the original collection will not be modified.





