 Backend Development
Backend Development
 C++
C++
 C/C++ program to calculate the number of trailing zeros in the factorial of a number
C/C++ program to calculate the number of trailing zeros in the factorial of a number
C/C++ program to calculate the number of trailing zeros in the factorial of a number
Here we will see how to calculate the number of trailing 0s in the factorial result of any number. So if n = 5, then 5! =120. There is only one trailing 0. For 20!, it would be 4 zeros as 20! = 2432902008176640000.
The simplest way is to calculate the factorial and calculate 0. But for larger values of n, this approach fails. So we're going to take another approach. If the prime factors are 2 and 5, then trailing zeros will appear. If we calculate 2 and 5, we get the result. To do this we will follow this rule.
Trailing 0 = Count of 5 in factorial(n) prime factors
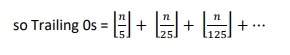
begin
count := 0
for i := 5, (n/i) >= 1, increase i := i * 5, do
count := count + (n / i)
done
return count;
endCopy after login## The Chinese translation of #Example
is: begin
count := 0
for i := 5, (n/i) >= 1, increase i := i * 5, do
count := count + (n / i)
done
return count;
endExample
#include <iostream>
#include <cmath>
#define MAX 20
using namespace std;
int countTrailingZeros(int n) {
int count = 0;
for (int i = 5; n / i >= 1; i *= 5)
count += n / i;
return count;
}
main() {
int n = 20;
cout << "Number of trailing zeros: " << countTrailingZeros(n);
}Output
Number of trailing zeros: 4
The above is the detailed content of C/C++ program to calculate the number of trailing zeros in the factorial of a number. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to calculate the factorial of n in C language
Jan 04, 2023 pm 03:18 PM
How to calculate the factorial of n in C language
Jan 04, 2023 pm 03:18 PM
How to calculate the factorial of n in C language: 1. Calculate the factorial through a for loop, with code such as "for (i = 1; i <= n; i++){fact *= i;}"; 2. Calculate the factorial through a while loop, Code such as "while (i <= n){fact *= i;i++;}"; 3. Calculate factorial recursively, code such as "int Fact(int n){int res = n;if (n > 1) res...".
 Factorial program in C program
Sep 09, 2023 am 11:17 AM
Factorial program in C program
Sep 09, 2023 am 11:17 AM
Givenwiththenumbernthetaskistocalculatethefactorialofanumber.Factorialofanumberiscalculatedbymultiplyingthenumberwithitssmallestorequalintegervalues.Factorialiscalculatedas−0!=11!=12!=2X1=23!=3X2X1=64!=4X3X2X1=245!=5X4X3X2X1=120...N!=n*(n-1
 What are the differences between php and c#
Jun 02, 2023 pm 01:45 PM
What are the differences between php and c#
Jun 02, 2023 pm 01:45 PM
The differences between php and c# are: 1. The language type system is different, PHP is dynamic, while C# is static type; 2. The platforms used are different, PHP can be cross-platform, while C# is exclusive to Windows; 3. The programming paradigm is different, PHP It supports object-oriented, procedural and functional programming, and C# is more inclined to object-oriented programming; 4. The execution speed is different, PHP is faster, and C# is relatively slow; 5. The application scenarios are different, PHP is used in web development, servers, etc. C# is used for Windows desktop and web applications.
 Why in C/C++, the sizeof of the structure is not equal to the sum of the sizeof of each member?
Aug 26, 2023 am 09:29 AM
Why in C/C++, the sizeof of the structure is not equal to the sum of the sizeof of each member?
Aug 26, 2023 am 09:29 AM
The size of the structure type elements obtained by sizeof() is not always equal to the size of each individual member. Sometimes the compiler adds some padding to avoid alignment problems. So dimensions may change. Padding is added when a structure member is followed by a member of larger size or is at the end of the structure. Different compilers have different types of alignment constraints. In the C standard, total alignment structures are implementation dependent. Case 1 In this case, the double z is 8 bytes long, which is larger than x (4 bytes)). So another 4 bytes of padding are added. Additionally, the short type data y has 2 bytes of space in memory, so an extra 6 bytes are added as padding. Sample code #include<stdio.h>structmyS
 Create a C/C++ code formatting tool using Clang tool
Aug 26, 2023 pm 01:09 PM
Create a C/C++ code formatting tool using Clang tool
Aug 26, 2023 pm 01:09 PM
In this tutorial, we willdiscussingaprogramtocreateaC/C++codeformattingtoolwiththehelpofclangtools.SETUPsudoaptinstallpythonsudoaptinstallclang-format-3.5 We will then create a Python file in a location where the current user has read and write permissions. Example importoscpp_extensions=(".cxx",".cpp&
 C/C++ programming to calculate the number of trailing zeros in the factorial of a number?
Sep 20, 2023 pm 10:05 PM
C/C++ programming to calculate the number of trailing zeros in the factorial of a number?
Sep 20, 2023 pm 10:05 PM
Calculating the number of trailing zeros in a factorial number is done by counting the number of 2's and 5's in the factors of the number. Because 2*5 is equal to 10, and 10 is the last zero in the factorial number. The factorial of Example 7 = 5040, and the number of 0s at the end is 1. According to our logic, 7!=2*3*4*5*6*7, which has 3 2s and 1 5, so the number of 0s at the end is 1. #include<iostream>usingnamespacestd;intmain(){ intn=45; intcount=0; &nb
![One article explains in detail vscode configuration C/C++ running environment [nanny-level teaching]](https://img.php.cn/upload/article/000/000/024/63fc94eb8852a975.jpg?x-oss-process=image/resize,m_fill,h_207,w_330) One article explains in detail vscode configuration C/C++ running environment [nanny-level teaching]
Feb 27, 2023 pm 07:33 PM
One article explains in detail vscode configuration C/C++ running environment [nanny-level teaching]
Feb 27, 2023 pm 07:33 PM
How to develop C/C++ in VScode? How to configure the C/C++ environment? The following article will share with you the VScode configuration C/C++ running environment tutorial (nanny-level teaching). I hope it will be helpful to you!
 In C/C++, there are two operations: pre-increment and post-increment.
Aug 25, 2023 pm 02:25 PM
In C/C++, there are two operations: pre-increment and post-increment.
Aug 25, 2023 pm 02:25 PM
Here we take a look at what are pre-increment and post-increment in C or C++. Both pre-increment and post-increment are increment operators. But there is little difference between them. The pre-increment operator first increments the value of a variable and then assigns it to other variables, but in the case of post-increment operator, it first assigns to a variable and then increments the value. Example #include<iostream>usingnamespacestd;main(){ intx,y,z; x=10; y=10;&nb





