 Backend Development
Backend Development
 C++
C++
 In C++, find the number of operations required to make all elements of an array equal
In C++, find the number of operations required to make all elements of an array equal
In C++, find the number of operations required to make all elements of an array equal

In this problem, we get an array arr of size n. Our task is to find the number of operations required to make all array elements equal. ##.
If it is not possible to make array elements equal, print -1.Let us take an example to understand this problem,
Input : arr[] = {7, 3, 3, 3}
Output : 3
The allocated array is {4, 4, 4 , 4}Solution
A simple way to solve this problem is to find the maximum value of the array. This maximum value is then used to check if all elements of the array are equal and if the value is equal to the maximum value of the array minus n (or a multiple thereof). If yes, n is returned, if no, -1 is returned (indicating that it is not possible).
Example
Let’s take an example to understand the problem
#include<bits/stdc++.h>
using namespace std;
int findOperationCount(int arr[],int n){
int j = 0, operations = 0;
int maxVal = arr[0];
int minVal = arr[0];
int maxValInd = 0;
for (int i = 1; i < n; i++){
if(arr[i] > maxVal){
maxVal = arr[i];
maxValInd = i;
}
if(arr[i] < minVal){
minVal = arr[i];
}
}
for (int i =0;i<n;i++){
if (arr[i] != maxVal && arr[i] <= minVal && arr[i] != 0){
arr[j] += 1;
arr[maxValInd] -= 1;
maxVal -= 1;
operations += 1;
j += 1;
}
else if (arr[i] != 0){
j += 1;
}
}
for (int i = 0; i < n; i++){
if (arr[i] != maxVal){
operations = -1;
break;
}
}
return operations;
}
int main(){
int arr[] = {4, 4, 8, 4};
int n = sizeof(arr)/sizeof(arr[0]);
cout<<"The number of operations required to make all array elements Equal is "<<findOperationCount(arr, n);
return 0;
}Output
The number of operations required to make all array elements Equal is 3
The above is the detailed content of In C++, find the number of operations required to make all elements of an array equal. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1392
1392
 52
52
 Use C++ to write code to find the Nth non-square number
Aug 30, 2023 pm 10:41 PM
Use C++ to write code to find the Nth non-square number
Aug 30, 2023 pm 10:41 PM
We all know numbers that are not the square of any number, such as 2, 3, 5, 7, 8, etc. There are N non-square numbers, and it is impossible to know every number. So, in this article, we will explain everything about squareless or non-square numbers and ways to find the Nth non-square number in C++. Nth non-square number If a number is the square of an integer, then the number is called a perfect square. Some examples of perfect square numbers are -1issquareof14issquareof29issquareof316issquareof425issquareof5 If a number is not the square of any integer, then the number is called non-square. For example, the first 15 non-square numbers are -2,3,5,6,
 Inversion algorithm for right rotation of array written in C++
Sep 08, 2023 pm 08:17 PM
Inversion algorithm for right rotation of array written in C++
Sep 08, 2023 pm 08:17 PM
In this article, we will learn about the reversal algorithm to rotate a given array to the right by k elements, for example −Input:arr[]={4,6,2,6,43,7,3,7},k= 4Output:{43,7,3,7,4,6,2,6}Explanation:Rotatingeachelementofarrayby4-elementtotherightgives{43,7,3,7,4,6,2,6}.Input:arr[]={8 ,5,8,2,1,4,9,3},k=3Output:{4,9,3,8,5,8,2,1} Find the solution
 In C programming, find the area of a circle
Aug 25, 2023 pm 10:57 PM
In C programming, find the area of a circle
Aug 25, 2023 pm 10:57 PM
A circle is a closed figure. All points on a circle are equidistant from a point inside the circle. The center point is called the center of the circle. The distance from a point to the center of a circle is called the radius. Area is a quantitative representation of the span of dimensions of a closed figure. The area of a circle is the area enclosed within the dimensions of the circle. The formula to calculate the area of a circle, Area=π*r*r To calculate the area, we give the radius of the circle as input, we will use the formula to calculate the area, algorithm STEP1: Takeradiusasinputfromtheuserusingstdinput.STEP2: Calculatetheareaofcircleusing, area=(
 Find the number of unique pairs in an array using C++
Sep 07, 2023 am 11:53 AM
Find the number of unique pairs in an array using C++
Sep 07, 2023 am 11:53 AM
We need proper knowledge to create several unique pairs in array syntax of C++. While finding the number of unique pairs, we count all the unique pairs in the given array i.e. all possible pairs can be formed where each pair should be unique. For example -Input:array[]={5,5,9}Output:4Explanation:Thenumberoffalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[]= {5,4,3,2,2}Output:16 Ways to Find Solution There are two ways to solve this problem, they are −
 Write a code using C++ to find the number of subarrays with the same minimum and maximum values
Aug 25, 2023 pm 11:33 PM
Write a code using C++ to find the number of subarrays with the same minimum and maximum values
Aug 25, 2023 pm 11:33 PM
In this article, we will use C++ to solve the problem of finding the number of subarrays whose maximum and minimum values are the same. The following is an example of the problem −Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6},{2 },{4},{4},{4},{6,6},{4,4},{4,4}and{4,4,4}arethesubarrayswhichcanbeformedwithmaximumandminimumelementsame.Input:array={3,3, 1,5,
 Written in C++, find the number of quadruples whose first three terms are arithmetic sequences and the last three terms are geometric sequences.
Aug 30, 2023 pm 02:09 PM
Written in C++, find the number of quadruples whose first three terms are arithmetic sequences and the last three terms are geometric sequences.
Aug 30, 2023 pm 02:09 PM
In this article we will describe all possible ways to find quaternions, using A.P. for the first 3 terms and G.P. for the last 3 terms. First, we will explain the basic definitions of arithmetic progression (A.P.) and geometric progression (G.P.). Arithmetic Progression (A.P.) - It is a sequence of numbers in which the common difference (d) is the same or constant, meaning that the difference of two consecutive numbers is constant. For example: 1,3,5,7,9|d=2 Geometric Progression (G.P.) - This is a sequence of numbers where the common ratio (r) is the same, which means we can multiply the previous number with a fixed number. For example: 3, 6, 12, 24, ....|r=2 In this problem, we need to determine how many are in the array arr[] of N integers
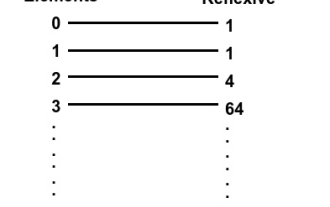 Written in C++, find the number of reflexive relations on a set
Aug 26, 2023 pm 08:17 PM
Written in C++, find the number of reflexive relations on a set
Aug 26, 2023 pm 08:17 PM
In this article we will explain ways to find reflexive relations on a set. In this problem, we are given a number n, and a set of n natural numbers, and we must determine the number of reflexive relations. Reflexive relation - A relation R is said to be a reflexive relation on the set A if for every 'a' in the set A, (a, a) belongs to the relation R. For example -Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*
 Reverse doubly linked list grouping by given size using C++
Sep 04, 2023 am 09:49 AM
Reverse doubly linked list grouping by given size using C++
Sep 04, 2023 am 09:49 AM
In this problem, we are given a pointer to the head of the linked list and an integer k. In a group of size k, we need to reverse the linked list. For example -Input:1<->2<->3<->4<->5(doublylinkedlist),k=3Output:3<->2<->1<->5<->4 looking for solutions Method In this problem, we will formulate a recursive algorithm to solve this problem. In this method we will use recursion and solve the problem using recursion. Example#include<iostream&



