What is an AA tree in C/C++?

In computer science, an AA tree is defined as a balanced tree implementation for efficient storage and retrieval of ordered data. AA trees are considered a variant of red-black trees, a binary search tree that supports efficient addition and deletion of entries. Unlike the red-black tree, the red node on the AA tree can only be added as a right child node and cannot be added as a left child node. The result of this operation is to simulate a 2-3 tree instead of a 2-3-4 tree, thus simplifying maintenance operations. The maintenance algorithm for red-black trees needs to assume or consider seven different shapes to correctly balance the tree.

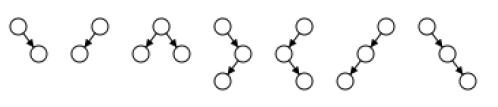
Contrary to the red-black tree, the AA tree only needs to assume or consider two shapes, since only the right link can be red.

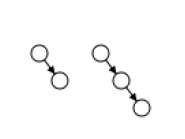
balanced rotation

Red-black trees require one balancing metadata bit (color) per node , while each node of the AA tree requires O(log(log(N))) metadata bits, in the form of integer "level". The following invariant applies to AA trees:

• The level of each leaf node is considered to be 1.

• The level of each left child node is 1 less than its parent node.

• The level of each right child node is equal to or 1 less than its parent node.

• The level of each right grandchild node is strictly smaller than that of its grandparent node.

• Every node with level greater than 1 has two child nodes.

Rebalancing an AA tree is much simpler than rebalancing a red-black tree.

In an AA tree, only two different operations are needed to restore balance: "skew" and "split". Skew is treated as a right rotation, replacing a subtree consisting of a left horizontal link with a right horizontal link. In the case of Split, it is left-turning and level-increasing, replacing a subtree containing two less consecutive right horizontal links with two or more consecutive right horizontal links. The two operations "skew" and "split" are explained below.

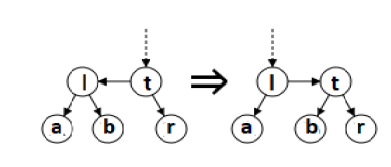
The definition of function skew is as follows:

   input: An AA tree that needs to be rebalanced is represented by a node, t.
   output: The rebalanced AA tree is represented by another node.
if nil(t) then
return nil
else if nil(left(t)) then
return t
else if level(left(t)) == level(t) then
   Exchange the pointers of horizontal left links.
   l = left(t)
left(t) := right(l)
right(l) := t
return l
else
return t
end if
end function

##The translation of function split is

is:

The function split is

   input: An AA tree that needs to be rebalanced is represented by a node, t.
   output: The rebalanced AA tree is represented by another node.
if nil(t) then
return nil
else if nil(right(t)) or nil(right(right(t))) then
return t
else if level(t) == level(right(right(t))) then
We have two horizontal right links. The middle node is taken, elevate it, and return it.
      r = right(t)
right(t) := left(r)
left(r) := t
level(r) := level(r) + 1
return r
else
return t
end if
end function

split-

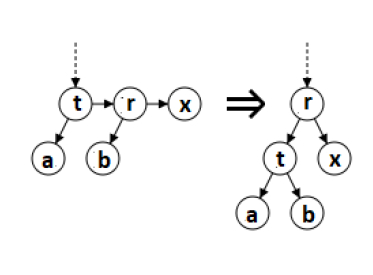
The above is the detailed content of What is an AA tree in C/C++?. For more information, please follow other related articles on the PHP Chinese website!