If no more than two points in the plane are collinear, what is the number of triangles?

Let's see how to count the number of triangles on a plane given n points, and limit the collinear points to no more than two.

Calculating the number of triangles in a plane with no more than two collinear points is a typical problem in computational geometry, which is applied in computer graphics, image processing, and other fields of computer science.

For example, when creating a 2D image from a 3D scene in 3D graphics, the problem may arise of calculating triangles in a plane with no more than two collinear points. In this case, the triangle counting process can be used to determine how many triangles are present in the final 2D image after projecting the 3D scene onto a plane. This allows you to determine the complexity of the scene and increase rendering speed.

In image processing, we may want to count the number of unique objects or shapes in an image, this problem is helpful. In this case, we can represent the image as a collection of points on a plane, and then we can count the number of triangles that can be created between these points by applying triangle counting techniques. We can determine the approximate number of different items or shapes in an image by counting the number of triangles formed.

illustrate

Let us understand this problem through a few examples and try to solve it. ​​

The purpose is to determine how many triangles are formed on a plane with n points such that no more than two points are collinear.

Example -

Assume N is the number of points on the plane.

N = 3

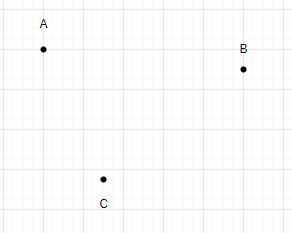
Using these points we can only draw a triangle.

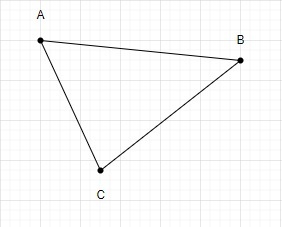
Therefore, the total number of triangles formed using 3 points is 1.

Let N = 4

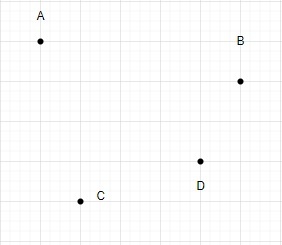
Let's draw a triangle using these four points.

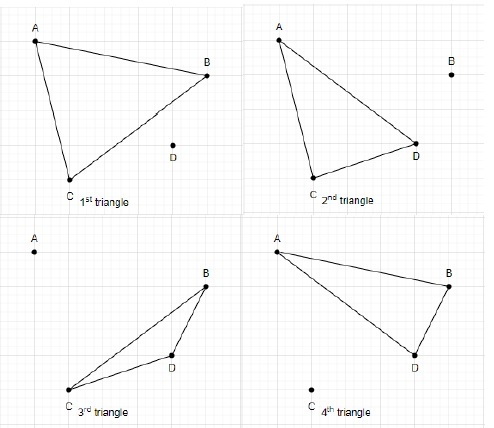
The total number of triangles formed using 4 points is 4.

Let's look at some of the math involved in calculating the number of triangles. This can be obtained using permutations and combinations. To build a triangle, you need 3 points out of the total at a time.

Thus, if a plane contains n points and no more than two of them are collinear, the number of triangles in the plane is given by the following formula.

$$\mathrm{n_{C_{3}}\:=\:\frac{n(n-1)\:(n-2)}{6}}$$

method

The program finds the number of triangles in the plane if no more than two points are collinear, using the following algorithm.

• Take the number of points on the plane as input and limit it to no more than two collinear points.

• Use the above formula to calculate the total number of triangles.

• Print the total number of triangles as output.

Example

C program to calculate the number of triangles in a plane if no more than two points are collinear.

#include <iostream>
using namespace std;

int main() {
   int number_of_points = 4;
   int number_of_triangle;
   
   number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
   cout << "Total number of triangles formed using " << number_of_points<< " points = " <<  number_of_triangle << endl;
   
   return 0;
}

Output

Total number of triangles formed using 4 points = 4

Complexity

Time complexity: O(1) because this code performs a fixed number of calculations regardless of the input size.

Space Complexity: O(1) because the code uses a fixed number of variables to store input values ​​and results regardless of the size of the input.

in conclusion

In this article, we try to explain the method to find the total number of possible triangles with n given points, with the constraint that no two points are collinear. I hope this article helps you learn this concept better.

The above is the detailed content of If no more than two points in the plane are collinear, what is the number of triangles?. For more information, please follow other related articles on the PHP Chinese website!