Space-optimized solution for LCS in C program?

Here we will see a spatial optimization method for the LCS problem. LCS is the longest common subsequence. If the two strings are "BHHUBC" and "HYUYBZC", then the length of the subsequence is 4. Dynamic programming method is already one of them, but using dynamic programming method will take up more space. We need a table of order m x n, where m is the number of characters in the first string and n is the number of characters in the second string.
Here we will learn how to use O(n) auxiliary space. If we look at the old approach, we can see that in each iteration, we need the data from the previous row. Not all data is required. So if we make a table of size 2n, that's no problem. Let's look at the algorithm to understand this idea.
Algorithm
lcs_problem(X, Y) -
begin
m := length of X
n := length of Y
define table of size L[2, n+1]
index is to point 0th or 1st row of the table L.
for i in range 1 to m, do
index := index AND 1
for j in range 0 to n, do
if i = 0 or j = 0, then
L[index, j] := 0
else if X[i - 1] = Y[j - 1], then
L[index, j] := L[1 – index, j - 1] + 1
else
L[index, j] := max of L[1 – index, j] and L[index, j-1]
end if
done
done
return L[index, n]
endExample
#include <iostream>
using namespace std;
int lcsOptimized(string &X, string &Y) {
int m = X.length(), n = Y.length();
int L[2][n + 1];
bool index;
for (int i = 0; i <= m; i++) {
index = i & 1;
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[index][j] = 0;
else if (X[i-1] == Y[j-1])
L[index][j] = L[1 - index][j - 1] + 1;
else
L[index][j] = max(L[1 - index][j], L[index][j - 1]);
}
}
return L[index][n];
}
int main() {
string X = "BHHUBC";
string Y = "HYUYBZC";
cout << "Length of LCS is :" << lcsOptimized(X, Y);
}Output
Length of LCS is :4
The above is the detailed content of Space-optimized solution for LCS in C program?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Translate the following into Chinese: C program to convert Roman numerals to decimal numbers
Sep 05, 2023 pm 09:53 PM
Translate the following into Chinese: C program to convert Roman numerals to decimal numbers
Sep 05, 2023 pm 09:53 PM
Given below is a C language algorithm to convert Roman numerals to decimal numbers: Algorithm Step 1 - Start Step 2 - Read Roman numerals at runtime Step 3 - Length: = strlen(roman) Step 4 - For i=0 to Length-1 Step 4.1-switch(roman[i]) Step 4.1.1-case'm': &nbs
 C++ program to compare the lexicographic order of two strings
Sep 04, 2023 pm 05:13 PM
C++ program to compare the lexicographic order of two strings
Sep 04, 2023 pm 05:13 PM
Lexicographic string comparison means that strings are compared in dictionary order. For example, if there are two strings 'apple' and 'appeal', the first string will come last because the first three characters of 'app' are the same. Then for the first string the character is 'l' and in the second string the fourth character is 'e'. Since 'e' is shorter than 'l', it will come first if we sort lexicographically. Strings are compared lexicographically before being arranged. In this article, we will see different techniques for lexicographically comparing two strings using C++. Using the compare() function in C++ strings The C++string object has a compare()
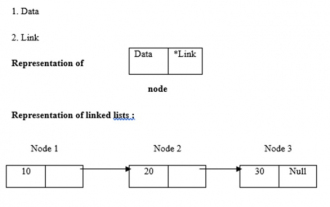 C program to find length of linked list
Sep 07, 2023 pm 07:33 PM
C program to find length of linked list
Sep 07, 2023 pm 07:33 PM
Linked lists use dynamic memory allocation, i.e. they grow and shrink accordingly. They are defined as collections of nodes. Here, a node has two parts, data and links. The representation of data, links and linked lists is as follows - Types of linked lists There are four types of linked lists, as follows: - Single linked list/Singly linked list Double/Doubly linked list Circular single linked list Circular double linked list We use the recursive method to find the length of the linked list The logic is -intlength(node *temp){ if(temp==NULL) returnl; else{&n
 C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
The rename function changes a file or directory from its old name to its new name. This operation is similar to the move operation. So we can also use this rename function to move files. This function exists in the stdio.h library header file. The syntax of the rename function is as follows: intrename(constchar*oldname,constchar*newname); The function of the rename() function accepts two parameters. One is oldname and the other is newname. Both parameters are pointers to constant characters that define the old and new names of the file. Returns zero if the file was renamed successfully; otherwise, returns a nonzero integer. During a rename operation
 C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
Hyperbolic functions are defined using hyperbolas instead of circles and are equivalent to ordinary trigonometric functions. It returns the ratio parameter in the hyperbolic sine function from the supplied angle in radians. But do the opposite, or in other words. If we want to calculate an angle from a hyperbolic sine, we need an inverse hyperbolic trigonometric operation like the hyperbolic inverse sine operation. This course will demonstrate how to use the hyperbolic inverse sine (asinh) function in C++ to calculate angles using the hyperbolic sine value in radians. The hyperbolic arcsine operation follows the following formula -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Where\:In\:is\:natural logarithm\:(log_e\:k)
 C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
A map is a special type of container in C++ in which each element is a pair of two values, namely a key value and a map value. The key value is used to index each item, and the mapped value is the value associated with the key. Regardless of whether the mapped value is unique, the key is always unique. To print map elements in C++ we have to use iterator. An element in a set of items is indicated by an iterator object. Iterators are primarily used with arrays and other types of containers (such as vectors), and they have a specific set of operations that can be used to identify specific elements within a specific range. Iterators can be incremented or decremented to reference different elements present in a range or container. The iterator points to the memory location of a specific element in the range. Printing a map in C++ using iterators First, let's look at how to define
 C++ program to check if a character is alphabetic or non-alphabetic
Sep 14, 2023 pm 03:37 PM
C++ program to check if a character is alphabetic or non-alphabetic
Sep 14, 2023 pm 03:37 PM
Using strings or characters is sometimes very useful when solving some logic programming problems. A string is a collection of characters, which is a 1-byte data type used to hold symbols in ASCII values. Symbols can be English letters, numbers, or special characters. In this article, we will learn how to check if a character is an English letter or a letter of the alphabet using C++. Checking the isalpha() function To check if a number is a letter, we can use the isalpha() function in the ctype.h header file. This takes a character as input and returns true if it is an alphabet, false otherwise. Let us look at the following C++ implementation to understand the usage of this function. The Chinese translation of Example is: show
 C++ program to get the imaginary part of a given complex number
Sep 06, 2023 pm 06:05 PM
C++ program to get the imaginary part of a given complex number
Sep 06, 2023 pm 06:05 PM
Modern science relies heavily on the concept of plural numbers, which was first established in the early 17th century by Girolamo Cardano, who introduced it in the 16th century. The formula for complex numbers is a+ib, where a holds the html code and b is a real number. A complex number is said to have two parts: the real part <a> and the imaginary part (<ib>). The value of i or iota is √-1. The plural class in C++ is a class used to represent complex numbers. The complex class in C++ can represent and control several complex number operations. Let's take a look at how to represent and control the display of plural numbers. imag() member function As mentioned above, complex numbers are composed of real part and imaginary part. To display the real part we use real()






