 Technology peripherals
Technology peripherals
 AI
AI
 The Thought Chain CoT evolved into the Thought Map GoT, and a prompt engineering technology better than the Thought Tree was born.
The Thought Chain CoT evolved into the Thought Map GoT, and a prompt engineering technology better than the Thought Tree was born.
The Thought Chain CoT evolved into the Thought Map GoT, and a prompt engineering technology better than the Thought Tree was born.
In order for large language models (LLM) to give full play to their capabilities, effective prompt design is essential. For this reason, the emerging field of prompt engineering has even emerged.
Among various prompt design solutions, Chain of Thinking (CoT) has attracted the attention of many researchers and users with its powerful reasoning capabilities. Based on its improved CoT-SC and further Thinking Tree (ToT) ) has also received a lot of attention.
Recently, a research team from ETH Zurich, Cledar and Warsaw University of Technology proposed a further idea: Maps of Mind (GoT). The ability to think from chains to trees to graphs and build a reasoning process for LLM has been continuously improved, and researchers have also proven this through experiments. They also released their own implementation of the GoT framework.

Research paper: https://arxiv.org/pdf/2308.09687v2.pdf
Official implementation: https://github.com/spcl /graph-of-thoughts
Paper Overview
Large-scale language models are becoming the dominant technology in the artificial intelligence world. The models that have developed rapidly in recent years are mainly based on decoder-only Transformer variants, such as GPT, PaLM or LLaMA.
When solving different LLM tasks, prompt engineering design is a method that can efficiently utilize resources. Simply put, a description of the task is included in the input sent to the LLM. If the task can be described in a suitable form, LLM can solve it with the help of its autoregressive token-based mechanism for generating text. Such prompts may contain example tasks with answers (few-shot prompt design, also known as contextual learning (ICL)), or they may not contain example tasks at all (zero-shot prompt design). Research and applications in recent years have shown that, This mechanism can be used to solve many types of tasks involving mathematics, common sense, or symbolic reasoning.
Chain of Thought (CoT) is a method used to design prompts, that is, in addition to the input of the task, the prompt In addition to output and output, it also includes intermediate steps of reasoning (intermediate thinking). Research shows that CoT can greatly improve the ability of LLM, enabling it to solve some difficult problems without any model updates.
Some researchers have also improved CoT proposes a method of using CoT to achieve self-consistency (CoT-SC); this solution is to generate multiple CoTs and then select the best result.
Recently, some researchers have further proposed thinking Tree (ToT), which models the LLM inference process through trees. This allows the model to use different thinking paths and can provide new functions, such as backtracking the inference process based on bad results. Unfortunately Unfortunately, since the ToT method imposes a strict tree structure on the thinking process, it will greatly limit prompt's reasoning ability. For more details, please refer to the article on this site "Thinking, thinking, thinking without stopping, Thinking Tree ToT" Military training "LLM" .
This research team from ETH Zurich, Cledar and Warsaw University of Technology believes that if the thinking of LLM can be constructed into an arbitrary graph structure, then it can provide prompt capabilities bring significant improvements. They said the idea was inspired by a variety of phenomena, such as the way humans reason, the structure of the brain, and the way algorithms execute.
Humans don’t behave like CoTs when thinking Following only one chain of thinking, instead of trying many different paths like ToT, will form a more complex network of thinking. For example, a person may first explore one chain of thinking, then backtrack and explore another, and then You may realize that an idea from the previous chain can be combined with the current chain to learn from each other and arrive at a new solution. Similarly, the brain will form complex networks, showing graph-like patterns, such as cyclic patterns. Algorithms The pattern of the network will also be revealed during execution, which can often be expressed as a directed acyclic graph.
The researchers said that if this corresponding graph-enabled transformation is used in LLM thinking, it is expected to create A powerful way to design prompts, but this transformation cannot be naturally expressed through CoT or ToT.
Then they observed: If the reasoning process of LLM is modeled as a graph, then it can be naturally Achieving these and many other thinking transformations. Based on this observation, they proposed GoT/Graph of Thoughts, a method that can enhance the capabilities of LLM through network-form reasoning.
In GoT, an LLM thought is modeled as a vertex, and the dependencies between vertices are modeled as edges. Using GoT, arbitrary ideas can be aggregated by constructing vertices with more than one input edge. Overall, the graph abstraction method used by GoT can seamlessly generalize CoT and ToT to more complex thinking models, and this process does not require updating the model.
However, to actually implement GoT, there are some design challenges that need to be solved. For example, what is the best graph structure for different tasks? What is the best approach to convergent thinking in order to maximize accuracy and minimize cost?
To answer these questions and more, these researchers designed a modular architecture for implementing GoT. The design has two major highlights.
First, it can achieve fine-grained control of each thinking. This gives users full control over conversations with LLM and the use of advanced thought transformations, such as combining the two most promising thoughts from an ongoing inference to get a new one.
The second is that this architecture is designed with scalability in mind - it can be seamlessly extended for new thinking transformations, reasoning modes (i.e., mind maps) and LLM models. This allows users to use GoT to quickly prototype new design ideas for prompt while experimenting with different models such as GPT-3.5, GPT-4 or Llama-2.
The researchers also demonstrated some use cases of GoT (sorting, keyword counting of summaries, set operations, document merging), and they also detailed how to implement them using a graph-based paradigm. They experimentally evaluate GoT, demonstrating its advantages over other state-of-the-art methods.
Researchers say that overall, GoT is particularly suitable for tasks that can be naturally decomposed into smaller subtasks, and these subtasks can be solved separately and then merged into a final solution. In this regard, GoT performs better than other solutions. For example, on the sorting task, GoT is better than CoT and ToT by about 70% and 62% respectively, while the cost is more than 31% lower than ToT.
Table 1 gives a qualitative comparison between GoT and other prompt design solutions. GoT is the only solution that can implement any graph-based thinking transformation (such as aggregation) within a prompt, thereby encompassing all previous solutions.

They also have another contribution, which is to propose a new evaluation metric - the volume of a thought, which can be used to evaluate prompt design strategies. The goal of using this metric, the researchers say, is to better understand the differences between prompt design options.
For a given thought v, the capacity of v refers to the number of LLM thoughts, based on which the user can use directed edges to obtain v. Intuitively, these are all the LLM ideas that are expected to contribute to v.
The author has shown through research that by integrating thinking transformation technologies such as aggregation, GoT can make the thinking capacity significantly larger than other solutions.
GoT Framework
The following is a detailed introduction to the GoT framework. The schematic diagram is shown in Figure 1, which also provides schematic diagrams of other prompt design strategies.

In mathematical form, GoT can be modeled as a tuple (G, T, E, R), where G is the LLM inference process (i.e. all the LLM thoughts and their relations), T is the possible thought transformations, E is the evaluator function used to obtain the thought score, and R is the ranking function used to select the most relevant thought.
Inference process
Here, the inference process is modeled as a directed graph G = (V, E), where V is a set of vertices, E ⊆ V × V is a set of edges. G is directed, so edges are subsets of ordered vertex pairs E ⊆ V × V . A vertex contains a solution to the current problem, whether it is the initial, intermediate, or final problem. The exact form of this thinking depends on the use case; it might be a piece of text (in a writing task) or a sequence of values (in a sorting task). The directed edge (t_1, t_2) represents the way the thought t_2 is constructed by using t_1 as "direct input", i.e. by explicitly instructing the LLM to use t_1 to generate t_2.
In some use cases, graph nodes belong to different categories. For example, in a writing task, some vertices model the plan for writing a text segment, while other nodes model the actual text segment. In this case, GoT adopts a heterogeneous graph G = (V, E, c) to model LLM inference, where c maps vertices V to their respective classes C (in the above case, C = {plan, par} ). This way, any vertex v can model different aspects of reasoning.
So G is associated with the LLM inference process. To facilitate this process, the user can use Thought Shift on G. An example of this kind of transformation: fuse the thought with the highest score so far into a new one. Another example is looping a thought in order to strengthen it. Note that these transformations strictly extend the set of transformations available in CoT, CoT-SC or ToT.
Thinking transformation
Thanks to the use of graph-based models for reasoning, GoT can achieve new thinking transformations. Researchers call this a graph-enabled transformation. For example, in a writing task multiple input articles can be combined into a coherent summary. When sorting, multiple sorted numeric subarrays can be combined into a final sorted array. Figure 2 gives an example of aggregation and generation.

Mathematically speaking, each such transformation can be modeled as T (G, p_θ), where G = (V, E) is the reflection of the current inference State diagram, p_θ is the LLM used. T usually modifies G by adding new vertices and their incoming edges. Then we have G′ = T (G, p_θ) = (V′, E′), where V′ = (V ∪ {V^ }) \ {V^−} and E′ = (E ∪ {E^ }) \{E^−}. V^ and E^ are new vertices and edges injected into G, which model new thinking and their dependencies respectively.
To maximize the expressive power of GoT, users can also delete thoughts by specifying the corresponding vertices and edges to be deleted (V^− and E^− respectively). Here, it is the user's responsibility to ensure that the sets V^ , E^ , V^− and E^− have consistent transformations (for example, the user will not try to delete non-existent vertices). This enables seamless integration of prompt solutions, where the user can remove non-improved parts of the reasoning to save space in the context.
The specific form of T and how it affects G depends on the specific transformation. The following will first introduce in detail the thinking transformations enabled by the main graphs, and then describe how GoT includes the transformations of previous solutions. Unless otherwise stated, V^− = E^− = ∅.
Aggregation Transformation: Users can use GoT to aggregate any thoughts into new thoughts to learn from each other's strengths. Here's a look at the basic form that only creates a new vertex: V^ = {v^ } and E^ = {(v_1, v^ ), ...,(v_k, v^ )}, where v_1, ..., v_k is the k thoughts being merged. More generally, this enables the aggregation of reasoning paths, i.e. longer chains of thoughts, rather than just individual thoughts. Using a graph model, an aggregation transformation can be easily implemented: by adding outgoing edges from vertices v_1, ..., v_k that model the last thought in several chains, to point to a single thought v^ that combines these chains.
Refining transformation: Another thinking transformation is to refine the current thinking v by modifying the content: V^ = {} and E^ = {(v, v)}. This loop in the diagram represents an iterative version of thinking that has the same connections as the original thought.
Generate transformation: Finally, the user can also generate one or more new thoughts based on an existing single thought v. Included in this category are similar reasoning steps from earlier schemes such as ToT or CoT-SC. Mathematically speaking, there Is the answer good enough? The score is modeled as a general function E (v, G, p_θ), where v is the thought being evaluated. In order to make E as general as possible, the whole process of reasoning (G) is also used in E, since in some assessment scenarios the scores may be related to other thinking.

System architecture and expansion capabilities
GoT consists of a set of interactive modules, see Figure 3 (blue part). These modules are Prompter (prepare messages for LLM), Parser (parser, extract information in LLM replies), Scoring module (validate LLM replies and score), Controller (controller, coordinate the entire reasoning process and decide how to proceed reasoning). Controller contains two other important components: graph of operations (GoO) and graph reasoning state (GRS). A GoO is a static structure that specifies the graph decomposition for a given task, i.e. it specifies the transformations applied to LLM thinking and their order and dependencies. The GRS is a dynamic structure that maintains the state of the ongoing LLM inference process (the history of its thinking and its states).Use case examples
The researcher describes some use cases of GoT, including sorting, set operations, keyword counting, and document merging ; Figure 4 below is an example of graph decomposition in GoT's sorting use case. We will not introduce the use cases in detail here, please refer to the original paper for details.


Latency vs. Capacity Tradeoff
Latency (how long it takes to reach a given final thought in the mind map The trade-off between hop count) and capacity is also very important, and researchers have shown that GoT is better than previous prompt designs on this trade-off. This paper defines a new metric - thought capacity, which is the number of previous LLM thoughts that can influence a given thought t. Mathematically, the capacity of thought t is the number of thoughts that have paths between t and t in the thought map. The researchers assumed that the cost of outputting a single thought is O (1) and fixed the total cost of each prompt solution as Θ(n).
The structure of various schemes is as follows. CoT-SC consists of k independent chains originating from a single starting thought. ToT is a complete k-ary tree. In GoT, a complete k-ary tree is added to its leaf nodes, with a "mirror" k-ary tree - the size is the same but the edges are reversed.
See Table 2 for detailed analysis. CoT has a larger capacity, up to N, but it also has a high latency cost of N. CoT-SC reduces latency by a factor of k (corresponding to its branching factor), but at the same time its capacity is reduced by a factor of k. The latency of ToT is log_k N, but the capacity is also low. GoT is the only solution that can achieve low latency log_k N and high capacity N. GoT is able to do this because it leverages thought aggregation, allowing it to arrive at the final thought from any other intermediate thoughts in the graph decomposition.

Evaluation
The researchers demonstrated the advantages of GoT over other solutions through experiments. The key comparison is between GoT and ToT, because the performance of ToT is already better than other solutions. Of course, they still did some experiments with IO, CoT and CoT-SC.
Figures 5 (sorting), 6 (set intersection), 7 (keyword counting), and 8 (document merging) show the experimental results.




The above is the detailed content of The Thought Chain CoT evolved into the Thought Map GoT, and a prompt engineering technology better than the Thought Tree was born.. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1382
1382
 52
52
 The author of ControlNet has another hit! The whole process of generating a painting from a picture, earning 1.4k stars in two days
Jul 17, 2024 am 01:56 AM
The author of ControlNet has another hit! The whole process of generating a painting from a picture, earning 1.4k stars in two days
Jul 17, 2024 am 01:56 AM
It is also a Tusheng video, but PaintsUndo has taken a different route. ControlNet author LvminZhang started to live again! This time I aim at the field of painting. The new project PaintsUndo has received 1.4kstar (still rising crazily) not long after it was launched. Project address: https://github.com/lllyasviel/Paints-UNDO Through this project, the user inputs a static image, and PaintsUndo can automatically help you generate a video of the entire painting process, from line draft to finished product. follow. During the drawing process, the line changes are amazing. The final video result is very similar to the original image: Let’s take a look at a complete drawing.
 Topping the list of open source AI software engineers, UIUC's agent-less solution easily solves SWE-bench real programming problems
Jul 17, 2024 pm 10:02 PM
Topping the list of open source AI software engineers, UIUC's agent-less solution easily solves SWE-bench real programming problems
Jul 17, 2024 pm 10:02 PM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com The authors of this paper are all from the team of teacher Zhang Lingming at the University of Illinois at Urbana-Champaign (UIUC), including: Steven Code repair; Deng Yinlin, fourth-year doctoral student, researcher
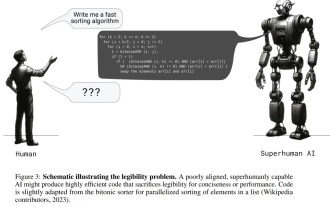 Posthumous work of the OpenAI Super Alignment Team: Two large models play a game, and the output becomes more understandable
Jul 19, 2024 am 01:29 AM
Posthumous work of the OpenAI Super Alignment Team: Two large models play a game, and the output becomes more understandable
Jul 19, 2024 am 01:29 AM
If the answer given by the AI model is incomprehensible at all, would you dare to use it? As machine learning systems are used in more important areas, it becomes increasingly important to demonstrate why we can trust their output, and when not to trust them. One possible way to gain trust in the output of a complex system is to require the system to produce an interpretation of its output that is readable to a human or another trusted system, that is, fully understandable to the point that any possible errors can be found. For example, to build trust in the judicial system, we require courts to provide clear and readable written opinions that explain and support their decisions. For large language models, we can also adopt a similar approach. However, when taking this approach, ensure that the language model generates
 From RLHF to DPO to TDPO, large model alignment algorithms are already 'token-level'
Jun 24, 2024 pm 03:04 PM
From RLHF to DPO to TDPO, large model alignment algorithms are already 'token-level'
Jun 24, 2024 pm 03:04 PM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com In the development process of artificial intelligence, the control and guidance of large language models (LLM) has always been one of the core challenges, aiming to ensure that these models are both powerful and safe serve human society. Early efforts focused on reinforcement learning methods through human feedback (RL
 arXiv papers can be posted as 'barrage', Stanford alphaXiv discussion platform is online, LeCun likes it
Aug 01, 2024 pm 05:18 PM
arXiv papers can be posted as 'barrage', Stanford alphaXiv discussion platform is online, LeCun likes it
Aug 01, 2024 pm 05:18 PM
cheers! What is it like when a paper discussion is down to words? Recently, students at Stanford University created alphaXiv, an open discussion forum for arXiv papers that allows questions and comments to be posted directly on any arXiv paper. Website link: https://alphaxiv.org/ In fact, there is no need to visit this website specifically. Just change arXiv in any URL to alphaXiv to directly open the corresponding paper on the alphaXiv forum: you can accurately locate the paragraphs in the paper, Sentence: In the discussion area on the right, users can post questions to ask the author about the ideas and details of the paper. For example, they can also comment on the content of the paper, such as: "Given to
 A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Aug 05, 2024 pm 03:32 PM
A significant breakthrough in the Riemann Hypothesis! Tao Zhexuan strongly recommends new papers from MIT and Oxford, and the 37-year-old Fields Medal winner participated
Aug 05, 2024 pm 03:32 PM
Recently, the Riemann Hypothesis, known as one of the seven major problems of the millennium, has achieved a new breakthrough. The Riemann Hypothesis is a very important unsolved problem in mathematics, related to the precise properties of the distribution of prime numbers (primes are those numbers that are only divisible by 1 and themselves, and they play a fundamental role in number theory). In today's mathematical literature, there are more than a thousand mathematical propositions based on the establishment of the Riemann Hypothesis (or its generalized form). In other words, once the Riemann Hypothesis and its generalized form are proven, these more than a thousand propositions will be established as theorems, which will have a profound impact on the field of mathematics; and if the Riemann Hypothesis is proven wrong, then among these propositions part of it will also lose its effectiveness. New breakthrough comes from MIT mathematics professor Larry Guth and Oxford University
 Axiomatic training allows LLM to learn causal reasoning: the 67 million parameter model is comparable to the trillion parameter level GPT-4
Jul 17, 2024 am 10:14 AM
Axiomatic training allows LLM to learn causal reasoning: the 67 million parameter model is comparable to the trillion parameter level GPT-4
Jul 17, 2024 am 10:14 AM
Show the causal chain to LLM and it learns the axioms. AI is already helping mathematicians and scientists conduct research. For example, the famous mathematician Terence Tao has repeatedly shared his research and exploration experience with the help of AI tools such as GPT. For AI to compete in these fields, strong and reliable causal reasoning capabilities are essential. The research to be introduced in this article found that a Transformer model trained on the demonstration of the causal transitivity axiom on small graphs can generalize to the transitive axiom on large graphs. In other words, if the Transformer learns to perform simple causal reasoning, it may be used for more complex causal reasoning. The axiomatic training framework proposed by the team is a new paradigm for learning causal reasoning based on passive data, with only demonstrations
 The first Mamba-based MLLM is here! Model weights, training code, etc. have all been open source
Jul 17, 2024 am 02:46 AM
The first Mamba-based MLLM is here! Model weights, training code, etc. have all been open source
Jul 17, 2024 am 02:46 AM
The AIxiv column is a column where this site publishes academic and technical content. In the past few years, the AIxiv column of this site has received more than 2,000 reports, covering top laboratories from major universities and companies around the world, effectively promoting academic exchanges and dissemination. If you have excellent work that you want to share, please feel free to contribute or contact us for reporting. Submission email: liyazhou@jiqizhixin.com; zhaoyunfeng@jiqizhixin.com. Introduction In recent years, the application of multimodal large language models (MLLM) in various fields has achieved remarkable success. However, as the basic model for many downstream tasks, current MLLM consists of the well-known Transformer network, which



