Program to calculate the area and perimeter of an equilateral triangle

A triangle is a closed figure with three sides. All sides of an equilateral triangle are equal. The area and perimeter of an equilateral triangle can be calculated using the following formula:
Area of an equilateral triangle = (√3)/4*a2
of an equilateral triangle Perimeter = 3 * a
Code Logic
To calculate the area of an equilateral triangle, the program uses the square root and power functions. The math library has these two functions that can be used to perform calculations in programs.
The following code shows the program to calculate the area and perimeter of an equilateral triangle,
Example
Live demonstration
#include <stdio.h>
#include <math.h>
int main(){
int side = 5, perimeter;
float area;
perimeter = (3 * side);
area = (sqrt(3)/4)*(side*side);
printf("perimeter is %d</p><p>", perimeter);
printf("area is %f", area);
return 0;
}Output
perimeter is 15 area is 10.825317
The above is the detailed content of Program to calculate the area and perimeter of an equilateral triangle. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
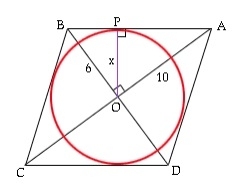 What is the area of a circle inscribed in a rhombus?
Sep 05, 2023 am 08:25 AM
What is the area of a circle inscribed in a rhombus?
Sep 05, 2023 am 08:25 AM
The inscribed circle of a rhombus is tangent to its four sides and four endpoints. The sides of the rhombus are tangent to the circle. Here, r is the radius found using a and the diagonal of the given value. Now the area triangle AOB = ½*OA*OB = ½*AB*r (both using the formula ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Circle area = π*r*r=π*(a2*b2)/4(a2support>+b2) Example of the diagonals of rhombus 5 and 10. Area is 15.700000 Example code Real-time demonstration #include<stdio.h>intma
 How to mark the area in CAD
Mar 14, 2023 am 11:30 AM
How to mark the area in CAD
Mar 14, 2023 am 11:30 AM
Method for area labeling in CAD: 1. Open CAD, click "Draw" to draw graphics; 2. Enter the "AREA" command and press Enter; 3. Select the area; 4. Press the space bar to display the area of the area; 5. Enter the command "T" and then enter the size of the area within the area.
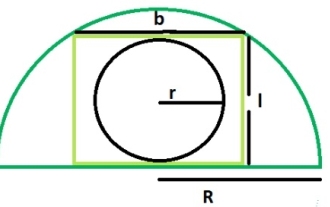 What is the area of a circle within a rectangle inscribed in a semicircle?
Sep 13, 2023 am 08:45 AM
What is the area of a circle within a rectangle inscribed in a semicircle?
Sep 13, 2023 am 08:45 AM
A circle inscribed in a rectangle is tangent to the longer side of the rectangle, that is, its length is tangent to the circle. A rectangle inscribed in a semicircle touches two points on the arc of the semicircle. The width of the rectangle is equal to the diameter of the circle. If R is the radius of the semicircle. The length of the rectangle = √2R/2 The width of the rectangle = R/√2 The radius of the inscribed circle is r = b/2 = R/2√2 Using this formula we can calculate the rectangle inscribed in the semicircle The area of a circle, area = (π*r2)=π*R/8 Example Demonstration #include<stdio.h>intmain(){&
 What is the area of the circular sector?
Aug 30, 2023 am 08:33 AM
What is the area of the circular sector?
Aug 30, 2023 am 08:33 AM
A circular sector, also known as a circular sector/sector of a circle, is a portion of a circle bounded by an arc between two radii. This area is bounded by two radii and an arc. To find the area inscribed, we need to find the angle between the two radii. The total area is equal to 360 degrees of angle. To find the area of an angle, we multiply the area by θ/360. This gives the area of the inscribed part. where θ is the angle (in degrees) between the two radii. The area of the circular sector = π*r*r*(θ/360). For example, the area of a circular sector with a radius of 5 and an angle of 60 degrees is 13.083. Area=(3.14*5*5)*(60/360)=13.03Example codeDemo#incl
 Find the area of a circle inscribed in a square in Java
Aug 19, 2023 pm 04:53 PM
Find the area of a circle inscribed in a square in Java
Aug 19, 2023 pm 04:53 PM
Acircleisaroundshapetwo-dimensionaldiagramwhichhasnocorners.Everycirclehasanoriginpointandeverypointonthecirclemaintainsequaldistancefromtheorigin.ThedistancebetweentheoriginandapointinacircleisknownasRadiusofthecircle.Andsimilarly,ifwedrawalinefromo
 How to measure the area of graphics in CAD Viewer. How to measure the area of graphics in CAD Viewer.
Mar 13, 2024 pm 01:43 PM
How to measure the area of graphics in CAD Viewer. How to measure the area of graphics in CAD Viewer.
Mar 13, 2024 pm 01:43 PM
How to measure the area of graphics in CAD Viewer? CAD Viewer is a very easy-to-use software for viewing engineering drawings. This software has many functions, and drawings in various formats can be opened and viewed. If when we look at the drawings, we find that the area measurement of some graphics is wrong or that some graphics forget to measure the area, we can use this software to measure the area of the graphics. So how to measure the area of graphics? Below, the editor of this site has compiled a CAD drawing king's steps to measure the area of graphics for your reference. Steps for measuring the graphic area in CAD Viewer 1. First, open the drawing file in CAD Viewer APP, take the drawing with arc graphics as an example, and measure the area of the graphic. 2. After opening the drawing, go to the bottom of the software interface
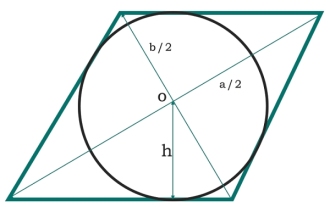 In the C program, what is the area of a circle inscribed in a rhombus?
Sep 01, 2023 pm 09:29 PM
In the C program, what is the area of a circle inscribed in a rhombus?
Sep 01, 2023 pm 09:29 PM
Here we will see the area of a circle inscribed in a rhombus. The diagonals of the rhombus are 'a' and 'b' respectively. The radius of the circle is h. Two diagonals form four equal triangles. Every triangle is a right triangle, so their area is - Each side of the rhombus is the hypotenuse - Therefore, the area of the circle is - Example#include<iostream>#include<cmath>usingnamespacestd;floatarea(floata,floatb) { if(a<0||b<0)//ifthevaluesaren
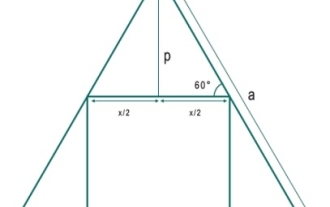 What is the largest square that can be inscribed in an equilateral triangle?
Sep 22, 2023 pm 06:21 PM
What is the largest square that can be inscribed in an equilateral triangle?
Sep 22, 2023 pm 06:21 PM
Here we will see the area of the largest square that can be inscribed in an equilateral triangle. The side length of the triangle is 'a' and the side length of the square is x. The side length 'a' of the triangle is − so x is − Example #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi




