
Suppose there is a weighted undirected graph with n vertices and m edges. The score of a graph is defined as the sum of the weights of all edges in the graph. Edge weights can be negative, and if they are removed, the graph's score will increase. What we need to do is to minimize the score of the graph by removing edges in the graph while maintaining the connectivity of the graph. We need to find the maximum score that can be reduced.
The graph is given in the form of an array 'edges', where each element is of the form {weight, {vertex1, vertex2}}.
So if the input is n = 5, m = 6, edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3} }, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}, then the output will be 4.
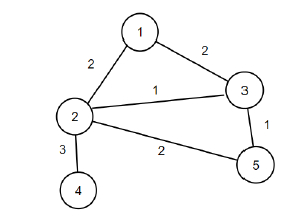
If we remove edges (1, 2) and (2, 5) from the graph, the total reduction in score will be 4 and the graph will still remain connected.
To solve this problem, we will follow the following steps:
cnum := 0
Define an array par of size: 100.
Define an array dim of size: 100.
Define a function make(), this will take v,
par[v] := v
dim[v] := 1
Define a function find(), this will take v,
if par[v] is same as v, then:
return v
return par[v] = find(par[v])
Define a function unify(), this will take a, b,
a := find(a)
b := find(b)
if a is not equal to b, then:
(decrease cnum by 1)
if dim[a] > dim[b], then:
swap values of (a, b)
par[a] := b
dim[b] := dim[b] + dim[a]
cnum := n
sort the array edges based on edge weights
for initialize i := 1, when i <= n, update (increase i by 1), do:
make(i)
res := 0
for each edge in edges, do:
a := first vertex of edge
b := second vertex of edge
weight := weight of edge
if find(a) is same as find(b), then:
if weight >= 0, then:
res := res + 1 * weight
Ignore following part, skip to the next iteration
if cnum is same as 1, then:
if weight >= 0, then:
res := res + 1 * weight
Otherwise
unify(a, b)
return resLet us see the following implementation for better understanding-
#include <bits/stdc++.h>
using namespace std;
int cnum = 0;
int par[100];
int dim[100];
void make(int v){
par[v] = v;
dim[v] = 1;
}
int find(int v){
if(par[v] == v)
return v;
return par[v] = find(par[v]);
}
void unify(int a, int b){
a = find(a); b = find(b);
if(a != b){
cnum--; if(dim[a] > dim[b]){
swap(a, b);
}
par[a] = b; dim[b] += dim[a];
}
}
int solve(int n, int m, vector <pair <int, pair<int,int>>> edges){
cnum = n;
sort(edges.begin(), edges.end());
for(int i = 1; i <= n; i++)
make(i);
int res = 0;
for(auto &edge : edges){
int a = edge.second.first;
int b = edge.second.second;
int weight = edge.first;
if(find(a) == find(b)) {
if(weight >= 0)
res += 1 * weight;
continue;
}
if(cnum == 1){
if(weight >= 0)
res += 1 * weight;
} else{
unify(a, b);
}
}
return res;
}
int main() {
int n = 5, m = 6;
vector <pair<int, pair<int,int>>> edges = {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}};
cout<< solve(n, m, edges);
return 0;
}5, 6, {{2, {1, 2}}, {2, {1, 3}}, {1, {2, 3}}, {3, {2, 4}}, {2, {2, 5}}, {1, {3, 5}}}
4
The above is the detailed content of C++ program to find the maximum score component that can be reduced from a graph. For more information, please follow other related articles on the PHP Chinese website!




