 Backend Development
Backend Development
 C++
C++
 C++ program to find out the minimum number of points needed to achieve a G score
C++ program to find out the minimum number of points needed to achieve a G score
C++ program to find out the minimum number of points needed to achieve a G score

Suppose we have two arrays p and c, each array has D elements, and there is another number G. Consider that in a programming competition, each question is scored based on its difficulty. The score of question p[i] is 100i. These p[1]...p[D] problems are all problems in the competition. Users on programming websites have a numerical total_score. The user's total_score is the sum of the following two elements.
Basic score: The sum of the scores of all problems solved
Reward: When When users solve all problems with a score of 100i, in addition to the basic score, they will also receive a perfect reward c[i].
Amal is new to the competition and has not solved any problems yet. His goal is to get an overall grade of G or more. We need to find out how many problems he needs to solve at least to reach this goal.
So if the input is G = 500; P = [3, 5]; C = [500, 800], then the output will be 3
Steps
For To solve this problem, we will follow the following steps:
D := size of p
mi := 10000
for initialize i := 0, when i < 1 << D, update (increase i by 1), do:
sum := 0
count := 0
at := 0
an array to store 10 bits b, initialize from bit value of i
for initialize j := 0, when j < D, update (increase j by 1), do:
if jth bit in b is 1, then:
count := p[j]
sum := sum + ((j + 1) * 100 * p[j] + c[j]
Otherwise
at := j
if sum < G, then:
d := (G - sum + (at + 1) * 100 - 1) / ((at + 1) * 100)
if d <= p[at], then:
sum := sum + (at + 1)
count := count + d
if sum >= G, then:
mi := minimum of mi and count
return miExample
Let us see the implementation below for better understanding −
#include <bits/stdc++.h>
using namespace std;
int solve(int G, vector<int> p, vector<int> c){
int D = p.size();
int mi = 10000;
for (int i = 0; i < 1 << D; i++){
int sum = 0;
int count = 0;
int at = 0;
bitset<10> b(i);
for (int j = 0; j < D; j++){
if (b.test(j)){
count += p.at(j);
sum += (j + 1) * 100 * p.at(j) + c.at(j);
} else {
at = j;
}
}
if (sum < G){
int d = (G - sum + (at + 1) * 100 - 1) / ((at + 1) * 100);
if (d <= p.at(at)){
sum += (at + 1) * 100 * d;
count += d;
}
}
if (sum >= G) {
mi = min(mi, count);
}
}
return mi;
}
int main() {
int G = 500;
vector<int> P = { 3, 5 };
vector<int> C = { 500, 800 };
cout << solve(G, P, C) << endl;
}Input
500, { 3, 5 }, { 500, 800 }Output
3
The above is the detailed content of C++ program to find out the minimum number of points needed to achieve a G score. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1377
1377
 52
52
 Translate the following into Chinese: C program to convert Roman numerals to decimal numbers
Sep 05, 2023 pm 09:53 PM
Translate the following into Chinese: C program to convert Roman numerals to decimal numbers
Sep 05, 2023 pm 09:53 PM
Given below is a C language algorithm to convert Roman numerals to decimal numbers: Algorithm Step 1 - Start Step 2 - Read Roman numerals at runtime Step 3 - Length: = strlen(roman) Step 4 - For i=0 to Length-1 Step 4.1-switch(roman[i]) Step 4.1.1-case'm': &nbs
 C++ program to compare the lexicographic order of two strings
Sep 04, 2023 pm 05:13 PM
C++ program to compare the lexicographic order of two strings
Sep 04, 2023 pm 05:13 PM
Lexicographic string comparison means that strings are compared in dictionary order. For example, if there are two strings 'apple' and 'appeal', the first string will come last because the first three characters of 'app' are the same. Then for the first string the character is 'l' and in the second string the fourth character is 'e'. Since 'e' is shorter than 'l', it will come first if we sort lexicographically. Strings are compared lexicographically before being arranged. In this article, we will see different techniques for lexicographically comparing two strings using C++. Using the compare() function in C++ strings The C++string object has a compare()
 How to calculate the score of the house in Misty Jianghu
Feb 29, 2024 pm 12:43 PM
How to calculate the score of the house in Misty Jianghu
Feb 29, 2024 pm 12:43 PM
There is a kind of house gameplay in Yanyu Jianghu. Players are free to build their own houses. After the house is successfully built, they will also get a house score. At the same time, the house score in the game also has its own calculation method. Of course, its calculation method is also It will be calculated using the given calculation method, and players can take a look. Calculation method of house score in Yanyujianghu 1. House score: appearance score, placement score, scale score, and research are divided into four parts. 2. Appearance score: mainly building skin bonus points and moving bonus points (200 points). There are two building skins. There are two types, one is the hand patch exchanged in the home shop above, and the other is the skin patch on the turntable. 3. Placement points: the points obtained by the crafted furniture, the green upper limit is 10 points, the blue upper limit is 15 points, and the purple upper limit is 10 points.
 How to insert fractions in word
Mar 19, 2024 pm 08:31 PM
How to insert fractions in word
Mar 19, 2024 pm 08:31 PM
There may be many people who don't know how to insert fractions into Word. After all, we don't often encounter the situation of entering fractions. But it will be more troublesome if you encounter it, so we should understand how to enter Word scores. Entering fractions in Word is actually very simple. Next, I will share how to enter fractions in Word. There are many ways to enter fractions in Word, one of which is to use the insert formula function. The steps are as follows: After opening the Word document, click the [Insert] option in the menu bar, and then select [Formula] in the pop-up menu. This will open a formula editor where you can enter the desired fraction. In the editor, you can use the fraction format buttons to create fractions, or manually enter "\frac{numerator}{
 C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
C++ program to find the value of the inverse hyperbolic sine function taking a given value as argument
Sep 17, 2023 am 10:49 AM
Hyperbolic functions are defined using hyperbolas instead of circles and are equivalent to ordinary trigonometric functions. It returns the ratio parameter in the hyperbolic sine function from the supplied angle in radians. But do the opposite, or in other words. If we want to calculate an angle from a hyperbolic sine, we need an inverse hyperbolic trigonometric operation like the hyperbolic inverse sine operation. This course will demonstrate how to use the hyperbolic inverse sine (asinh) function in C++ to calculate angles using the hyperbolic sine value in radians. The hyperbolic arcsine operation follows the following formula -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Where\:In\:is\:natural logarithm\:(log_e\:k)
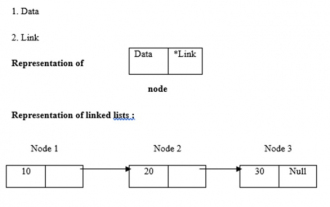 C program to find length of linked list
Sep 07, 2023 pm 07:33 PM
C program to find length of linked list
Sep 07, 2023 pm 07:33 PM
Linked lists use dynamic memory allocation, i.e. they grow and shrink accordingly. They are defined as collections of nodes. Here, a node has two parts, data and links. The representation of data, links and linked lists is as follows - Types of linked lists There are four types of linked lists, as follows: - Single linked list/Singly linked list Double/Doubly linked list Circular single linked list Circular double linked list We use the recursive method to find the length of the linked list The logic is -intlength(node *temp){ if(temp==NULL) returnl; else{&n
 C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
C++ program to print dictionary
Sep 11, 2023 am 10:33 AM
A map is a special type of container in C++ in which each element is a pair of two values, namely a key value and a map value. The key value is used to index each item, and the mapped value is the value associated with the key. Regardless of whether the mapped value is unique, the key is always unique. To print map elements in C++ we have to use iterator. An element in a set of items is indicated by an iterator object. Iterators are primarily used with arrays and other types of containers (such as vectors), and they have a specific set of operations that can be used to identify specific elements within a specific range. Iterators can be incremented or decremented to reference different elements present in a range or container. The iterator points to the memory location of a specific element in the range. Printing a map in C++ using iterators First, let's look at how to define
 C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
C program uses rename() function to change file name
Sep 21, 2023 pm 10:01 PM
The rename function changes a file or directory from its old name to its new name. This operation is similar to the move operation. So we can also use this rename function to move files. This function exists in the stdio.h library header file. The syntax of the rename function is as follows: intrename(constchar*oldname,constchar*newname); The function of the rename() function accepts two parameters. One is oldname and the other is newname. Both parameters are pointers to constant characters that define the old and new names of the file. Returns zero if the file was renamed successfully; otherwise, returns a nonzero integer. During a rename operation



