How to implement gradient descent algorithm in Python to find local minima?

Gradient descent is an important optimization method in machine learning, used to minimize the loss function of the model. In layman's terms, it requires repeatedly changing the parameters of the model until the ideal value range that minimizes the loss function is found. The method works by taking tiny steps in the direction of the negative gradient of the loss function, or more specifically, along the path of steepest descent. The learning rate is a hyperparameter that regulates the trade-off between algorithm speed and accuracy, and it affects the size of the step size. Many machine learning methods, including linear regression, logistic regression, and neural networks, to name a few, employ gradient descent. Its main application is model training, where the goal is to minimize the difference between the expected and actual values ​​of the target variable. In this article, we will look at implementing gradient descent in Python to find local minima.

Now it’s time to implement gradient descent in Python. Here's a basic description of how we implement it -

• First, we import the necessary libraries.

• Define its function and its derivatives.

• Next, we will apply the gradient descent function.

• After applying the function, we will set the parameters to find the local minimum,

• Finally, we will plot the output.

Implementing Gradient Descent in Python

Import library

import numpy as np
import matplotlib.pyplot as plt

Then we define the function f(x) and its derivative f'(x) -

def f(x):
   return x**2 - 4*x + 6

def df(x):
   return 2*x - 4

F(x) is the function that must be reduced and df is its derivative (x). The gradient descent method uses derivatives to guide itself toward the minimum by revealing the slope of the function along the way.

Then define the gradient descent function.

def gradient_descent(initial_x, learning_rate, num_iterations):
   x = initial_x
   x_history = [x]
  
   for i in range(num_iterations):
       gradient = df(x)
       x = x - learning_rate * gradient
       x_history.append(x)
      
   return x, x_history

The starting value of x, the learning rate and the required number of iterations are sent to the gradient descent function. To save the value of x after each iteration, it initializes x to its original value and generates an empty list. The method then performs gradient descent for the provided number of iterations, changing x in each iteration according to the equation x = x - learning rate * gradient. This function generates a list of x values ​​for each iteration and the final value of x.

The gradient descent function can now be used to locate the local minimum of f(x) -

Example

initial_x = 0
learning_rate = 0.1
num_iterations = 50

x, x_history = gradient_descent(initial_x, learning_rate, num_iterations)

print("Local minimum: {:.2f}".format(x))

Output

Local minimum: 2.00

In this figure, x is initially set to 0, the learning rate is 0.1, and 50 iterations are run. Finally, we publish the value of x, which should be close to the local minimum at x=2.

Plotting the function f(x) and the x value for each iteration allows us to see the gradient descent process in action -

Example

# Create a range of x values to plot
x_vals = np.linspace(-1, 5, 100)

# Plot the function f(x)
plt.plot(x_vals, f(x_vals))

# Plot the values of x at each iteration
plt.plot(x_history, f(np.array(x_history)), 'rx')

# Label the axes and add a title
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')

# Show the plot
plt.show()

Output

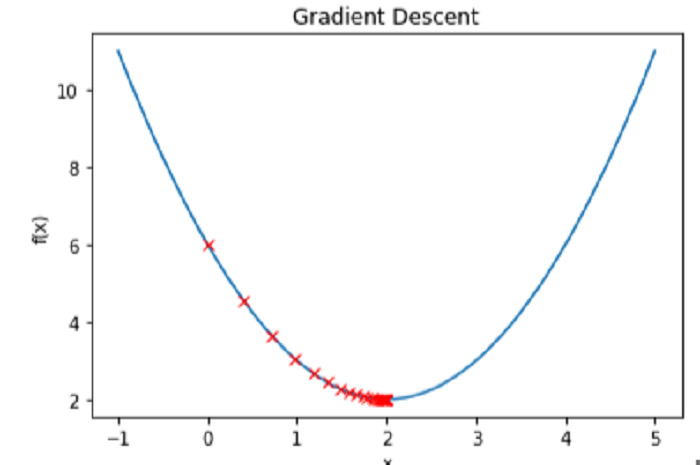
in conclusion

In summary, to find the local minimum of a function, Python utilizes an efficient optimization process called gradient descent. Gradient descent works by computing the derivative of a function at each step, repeatedly updating input values ​​in the direction of steepest descent until the lowest value is reached. Implementing gradient descent in Python requires specifying the function to be optimized and its derivatives, initializing input values, and determining the learning rate and number of iterations of the algorithm. After optimization is complete, the method can be evaluated by tracing its steps to the minimum and seeing how it reaches that goal. Gradient descent is a useful technique in machine learning and optimization applications because Python can handle large data sets and complex functions.

The above is the detailed content of How to implement gradient descent algorithm in Python to find local minima?. For more information, please follow other related articles on the PHP Chinese website!