In C, the largest Reuleaux triangle inside a square
A Lule Triangle is a shape formed by the intersection of three disks, with the center of each disk on the boundary of the other two disks. Its boundary is a curve of constant width, and apart from the circle itself, it is the simplest and best-known such curve. Constant width means that the spacing between each two parallel support lines is the same, regardless of their orientation. Because all its diameters are the same.
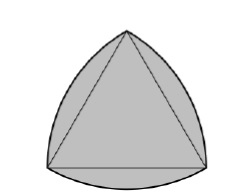
The boundary of the Lule triangle is a constant-width curve based on an equilateral triangle. All points on an edge are equidistant from the opposite vertex.
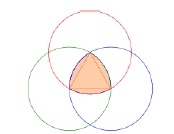
Construct a Lule triangle
The formula of Lule triangle
If the curve is based on an equilateral triangle, the side length of the triangle is h , then the area of the Reuleaux triangle is
A = (π * h<sup>2</sup>) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h<sup>2</sup> / 2 = 0.70477 * h<sup>2</sup>
Find the largest Reuleaux triangle inside a square
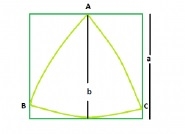
Let us give an example,
Input: a = 6 Output: 25.3717
Explanation
The area of Reuleaux triangle is 0.70477 * b2, where b is the distance between parallel lines Support Reuleaux triangle .
The distance between the parallel lines supporting the Reuleaux triangle = the side length of the square, that is, a
The area of the Reuleaux triangle, A = 0.70477 * a2
##Example#include <stdio.h>
#include <math.h>
int main() {
float a = 6;
float area = 0.70477 * pow(a, 2);
printf("The area is : %f",area);
return 0;
}Copy after login
Output#include <stdio.h>
#include <math.h>
int main() {
float a = 6;
float area = 0.70477 * pow(a, 2);
printf("The area is : %f",area);
return 0;
}The area is : 25.371719
Copy after login
The area is : 25.371719
The above is the detailed content of In C, the largest Reuleaux triangle inside a square. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 C language data structure: data representation and operation of trees and graphs
Apr 04, 2025 am 11:18 AM
C language data structure: data representation and operation of trees and graphs
Apr 04, 2025 am 11:18 AM
C language data structure: The data representation of the tree and graph is a hierarchical data structure consisting of nodes. Each node contains a data element and a pointer to its child nodes. The binary tree is a special type of tree. Each node has at most two child nodes. The data represents structTreeNode{intdata;structTreeNode*left;structTreeNode*right;}; Operation creates a tree traversal tree (predecision, in-order, and later order) search tree insertion node deletes node graph is a collection of data structures, where elements are vertices, and they can be connected together through edges with right or unrighted data representing neighbors.
 The truth behind the C language file operation problem
Apr 04, 2025 am 11:24 AM
The truth behind the C language file operation problem
Apr 04, 2025 am 11:24 AM
The truth about file operation problems: file opening failed: insufficient permissions, wrong paths, and file occupied. Data writing failed: the buffer is full, the file is not writable, and the disk space is insufficient. Other FAQs: slow file traversal, incorrect text file encoding, and binary file reading errors.
 C language multithreaded programming: a beginner's guide and troubleshooting
Apr 04, 2025 am 10:15 AM
C language multithreaded programming: a beginner's guide and troubleshooting
Apr 04, 2025 am 10:15 AM
C language multithreading programming guide: Creating threads: Use the pthread_create() function to specify thread ID, properties, and thread functions. Thread synchronization: Prevent data competition through mutexes, semaphores, and conditional variables. Practical case: Use multi-threading to calculate the Fibonacci number, assign tasks to multiple threads and synchronize the results. Troubleshooting: Solve problems such as program crashes, thread stop responses, and performance bottlenecks.
 CS-Week 3
Apr 04, 2025 am 06:06 AM
CS-Week 3
Apr 04, 2025 am 06:06 AM
Algorithms are the set of instructions to solve problems, and their execution speed and memory usage vary. In programming, many algorithms are based on data search and sorting. This article will introduce several data retrieval and sorting algorithms. Linear search assumes that there is an array [20,500,10,5,100,1,50] and needs to find the number 50. The linear search algorithm checks each element in the array one by one until the target value is found or the complete array is traversed. The algorithm flowchart is as follows: The pseudo-code for linear search is as follows: Check each element: If the target value is found: Return true Return false C language implementation: #include#includeintmain(void){i
 How to output a countdown in C language
Apr 04, 2025 am 08:54 AM
How to output a countdown in C language
Apr 04, 2025 am 08:54 AM
How to output a countdown in C? Answer: Use loop statements. Steps: 1. Define the variable n and store the countdown number to output; 2. Use the while loop to continuously print n until n is less than 1; 3. In the loop body, print out the value of n; 4. At the end of the loop, subtract n by 1 to output the next smaller reciprocal.
 C language data structure: the key role of data structures in artificial intelligence
Apr 04, 2025 am 10:45 AM
C language data structure: the key role of data structures in artificial intelligence
Apr 04, 2025 am 10:45 AM
C Language Data Structure: Overview of the Key Role of Data Structure in Artificial Intelligence In the field of artificial intelligence, data structures are crucial to processing large amounts of data. Data structures provide an effective way to organize and manage data, optimize algorithms and improve program efficiency. Common data structures Commonly used data structures in C language include: arrays: a set of consecutively stored data items with the same type. Structure: A data type that organizes different types of data together and gives them a name. Linked List: A linear data structure in which data items are connected together by pointers. Stack: Data structure that follows the last-in first-out (LIFO) principle. Queue: Data structure that follows the first-in first-out (FIFO) principle. Practical case: Adjacent table in graph theory is artificial intelligence
 Concept of c language function
Apr 03, 2025 pm 10:09 PM
Concept of c language function
Apr 03, 2025 pm 10:09 PM
C language functions are reusable code blocks. They receive input, perform operations, and return results, which modularly improves reusability and reduces complexity. The internal mechanism of the function includes parameter passing, function execution, and return values. The entire process involves optimization such as function inline. A good function is written following the principle of single responsibility, small number of parameters, naming specifications, and error handling. Pointers combined with functions can achieve more powerful functions, such as modifying external variable values. Function pointers pass functions as parameters or store addresses, and are used to implement dynamic calls to functions. Understanding function features and techniques is the key to writing efficient, maintainable, and easy to understand C programs.
 The concept of c language functions and their definition format
Apr 03, 2025 pm 11:33 PM
The concept of c language functions and their definition format
Apr 03, 2025 pm 11:33 PM
C language functions are reusable code blocks, receive parameters for processing, and return results. It is similar to the Swiss Army Knife, powerful and requires careful use. Functions include elements such as defining formats, parameters, return values, and function bodies. Advanced usage includes function pointers, recursive functions, and callback functions. Common errors are type mismatch and forgetting to declare prototypes. Debugging skills include printing variables and using a debugger. Performance optimization uses inline functions. Function design should follow the principle of single responsibility. Proficiency in C language functions can significantly improve programming efficiency and code quality.




