C++ program to calculate the base 10 logarithm of a given value

Natural calculations in a variety of applications require base 10 logarithms. For competitive exams, there are some quick ways to remember some log values. When programming, there are several ways to calculate logarithmic results using library functions as well as some shortcuts. In this article, we will introduce several ways to calculate the base 10 logarithm of a given number in C.
Use log10() function
The library function used to determine the base 10 logarithm of a given argument is called log10(). The response can be an integer or a float. Using this method is very simple; all you have to do is call the function with a single integer argument and the cmath library and let it calculate the base 10 logarithm for you. Let's look at the syntax and related procedures to see how it is used.
grammar
#include < cmath > log2( <number> )
algorithm
- Take the number x as input
- Use log10(x) to calculate the base 10 logarithm of x
- Return results.
Example
#include <iostream>
#include <cmath>
using namespace std;
float solve( int x ){
float answer;
answer = log10( x );
return answer;
}
int main(){
cout << "Log base 10 for input x = 100 is: " << solve( 100 ) << endl;
cout << "Log base 10 for input x = 1000 is: " << solve( 1000 ) << endl;
cout << "Log base 10 for input x = 5487 is: " << solve( 5487 ) << endl;
cout << "Log base 10 for input x = 25479 is: " << solve( 25479 ) << endl;
}
Output
Log base 10 for input x = 100 is: 2 Log base 10 for input x = 1000 is: 3 Log base 10 for input x = 5487 is: 3.73934 Log base 10 for input x = 25479 is: 4.40618
Use logarithmic functions with other bases
Some interesting characteristics of logarithms. We can calculate from any base the logarithmic output of another base. To calculate using any logarithmic base, use the following formula.
$$\mathrm{log_{10}\left ( x \right )=\frac{log_{k}\left ( x \right )}{log_{k}\left ( 10 \right )}}$ $
algorithm
- Take the number x as input
- nume := log-base-k ( x )
- deno := log-base-k(10)
- Return (nume/deno).
Example
#include <iostream>
#include <cmath>
using namespace std;
float solve( int x ){
float nume, deno;
nume = log( x );
deno = log( 10 );
return nume / deno;
}
int main(){
cout << "Log base 10 for input x = 100 is: " << solve( 100 ) << endl;
cout << "Log base 10 for input x = 1000 is: " << solve( 1000 ) << endl;
cout << "Log base 10 for input x = 5487 is: " << solve( 5487 ) << endl;
cout << "Log base 10 for input x = 25479 is: " << solve( 25479 ) << endl;
}
Output
Log base 10 for input x = 100 is: 2 Log base 10 for input x = 1000 is: 3 Log base 10 for input x = 5487 is: 3.73933 Log base 10 for input x = 25479 is: 4.40618
in conclusion
The log10() method of the cmath package can be used to calculate the base 10 logarithm. The result will be returned as an integer or fraction. Another approach is to use a different logarithmic base and a simple logarithmic formula, as shown in Part II. To obtain more accurate results, we can also use numerical methods to calculate logarithmic results using the bisection method, Newton-Raphson method, or any other nonlinear equation solving technique.
The above is the detailed content of C++ program to calculate the base 10 logarithm of a given value. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 37
37
 110
110
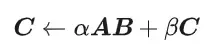 CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
CUDA's universal matrix multiplication: from entry to proficiency!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) is a vital part of many applications and algorithms, and is also one of the important indicators for evaluating computer hardware performance. In-depth research and optimization of the implementation of GEMM can help us better understand high-performance computing and the relationship between software and hardware systems. In computer science, effective optimization of GEMM can increase computing speed and save resources, which is crucial to improving the overall performance of a computer system. An in-depth understanding of the working principle and optimization method of GEMM will help us better utilize the potential of modern computing hardware and provide more efficient solutions for various complex computing tasks. By optimizing the performance of GEMM
 How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
How to calculate addition, subtraction, multiplication and division in word document
Mar 19, 2024 pm 08:13 PM
WORD is a powerful word processor. We can use word to edit various texts. In Excel tables, we have mastered the calculation methods of addition, subtraction and multipliers. So if we need to calculate the addition of numerical values in Word tables, How to subtract the multiplier? Can I only use a calculator to calculate it? The answer is of course no, WORD can also do it. Today I will teach you how to use formulas to calculate basic operations such as addition, subtraction, multiplication and division in tables in Word documents. Let's learn together. So, today let me demonstrate in detail how to calculate addition, subtraction, multiplication and division in a WORD document? Step 1: Open a WORD, click [Table] under [Insert] on the toolbar, and insert a table in the drop-down menu.
 How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to count the number of elements in a list using Python's count() function
Nov 18, 2023 pm 02:53 PM
How to use Python's count() function to calculate the number of an element in a list requires specific code examples. As a powerful and easy-to-learn programming language, Python provides many built-in functions to handle different data structures. One of them is the count() function, which can be used to count the number of elements in a list. In this article, we will explain how to use the count() function in detail and provide specific code examples. The count() function is a built-in function of Python, used to calculate a certain
 Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Java program to calculate the area of a triangle using determinants
Aug 31, 2023 am 10:17 AM
Introduction The Java program for calculating the area of a triangle using determinants is a concise and efficient program that can calculate the area of a triangle given the coordinates of three vertices. This program is useful for anyone learning or working with geometry, as it demonstrates how to use basic arithmetic and algebraic calculations in Java, as well as how to use the Scanner class to read user input. The program prompts the user for the coordinates of three points of the triangle, which are then read in and used to calculate the determinant of the coordinate matrix. Use the absolute value of the determinant to ensure the area is always positive, then use a formula to calculate the area of the triangle and display it to the user. The program can be easily modified to accept input in different formats or to perform additional calculations, making it a versatile tool for geometric calculations. ranks of determinants
 Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Count the number of occurrences of a substring recursively in Java
Sep 17, 2023 pm 07:49 PM
Given two strings str_1 and str_2. The goal is to count the number of occurrences of substring str2 in string str1 using a recursive procedure. A recursive function is a function that calls itself within its definition. If str1 is "Iknowthatyouknowthatiknow" and str2 is "know" the number of occurrences is -3. Let us understand through examples. For example, input str1="TPisTPareTPamTP", str2="TP"; output Countofoccurrencesofasubstringrecursi
 How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
How to use the Math.Pow function in C# to calculate the power of a specified number
Nov 18, 2023 am 11:32 AM
In C#, there is a Math class library, which contains many mathematical functions. These include the function Math.Pow, which calculates powers, which can help us calculate the power of a specified number. The usage of the Math.Pow function is very simple, you only need to specify the base and exponent. The syntax is as follows: Math.Pow(base,exponent); where base represents the base and exponent represents the exponent. This function returns a double type result, that is, the power calculation result. Let's
 Python program to calculate the sum of the right diagonal elements of a matrix
Aug 19, 2023 am 11:29 AM
Python program to calculate the sum of the right diagonal elements of a matrix
Aug 19, 2023 am 11:29 AM
A popular general-purpose programming language is Python. It is used in a variety of industries, including desktop applications, web development, and machine learning. Fortunately, Python has a simple and easy-to-understand syntax that is suitable for beginners. In this article, we will use Python to calculate the sum of the right diagonal of a matrix. What is a matrix? In mathematics, we use a rectangular array or matrix to describe a mathematical object or its properties. It is a rectangular array or table containing numbers, symbols, or expressions arranged in rows and columns. . For example -234512367574 Therefore, this is a matrix with 3 rows and 4 columns, expressed as a 3*4 matrix. Now, there are two diagonals in the matrix, the primary diagonal and the secondary diagonal
 Java program example to calculate total score and percentage
Sep 11, 2023 pm 06:01 PM
Java program example to calculate total score and percentage
Sep 11, 2023 pm 06:01 PM
We will demonstrate how to calculate total scores and percentages using a Java program. Total score refers to the sum of all available scores, while the term percentage refers to the calculated score divided by the total score and multiplied by the resulting number 100. percentage_of_marks=(obtained_marks/total_marks)×100 Example 1 This is a Java program that demonstrates how to calculate total scores and percentages. //JavaProgramtodemonstratehowisTotalmarksandPercentagescalculatedimportjava.io.*;publicclassTotalMarks_




