 Backend Development
Backend Development
 C++
C++
 The longest subsequence whose characters are the same as the substring and whose frequency difference is at most K
The longest subsequence whose characters are the same as the substring and whose frequency difference is at most K
The longest subsequence whose characters are the same as the substring and whose frequency difference is at most K

In this problem, we will find the maximum length of the subsequence such that it contains consecutive characters and the frequency difference of all characters does not exceed K.
We need to find all possible subsequences of a given string and check if it contains each character consecutively and with maximum frequency difference to get the output.
Problem Statement- We are given a string alpha containing lowercase alphabetic characters. Additionally, we have been given a positive integer K. We need to find the maximum length of a subsequence of a given string such that it follows the following rules.
All occurrences of a specific character should be consecutive.
The difference in frequency of characters cannot be greater than K.
Example
enter
alpha = "ppppqrs", K = 2
Output
6
Explanation - We can take the "pppqrs" subsequence. The maximum character frequency is 3 and the minimum character frequency is 1. Therefore, the difference is 2. And it contains all characters consecutively.
enter
alpha = "abbbbc", K = 2
Output
5
Explanation - We can take the "abbbc" subsequence.
enter
alpha = "mnnnnnnno", k = 3;
Output
7
Explanation - We can take the "nnnnnnn" subsequence.
method 1
In this method, we will use a recursive function to find all subsequences of a given length. Additionally, we will define functions to check if a subsequence contains all characters consecutively. We will use the map data structure to calculate the maximum and minimum frequency differences.
algorithm
Step 1 - Define the "f" mapping to store the frequency of characters.
Step 2 - If start is equal to the length of the temporary string, and the string length is greater than 0, follow these steps.
Step 3 - Initialize the "minf" and "maxf" variables to store the minimum and maximum frequencies.
Step 4 - Clear the map and store the frequency of each character in the map.
Step 5 - Loop through the map values and find the maximum and minimum frequency values.
Step 6 - If the maximum and minimum frequency difference is less than or equal to K, check whether the string contains consecutive characters.
Step 6.1 - In the checkForContinously() function, define the "pos" map to store the last position of a specific character.
Step 6.2 - Traverse the string. If the current character exists in the map and the difference between the character's current position and last position is less than 1, update the last position. Otherwise, returns false.
Step 6.3 - Add the character to the map if it does not exist.
Step 6.4 - Finally return true.
Step 7 - If the string contains consecutive characters and the frequency difference is less than K, if the value of 'maxi' is less than the length of the current subsequence, update the value of 'maxi'.
Step 8 - Make a recursive call after excluding the current character.
Step 9 - Append the current characters to the end of the temporary string. Also, make a recursive call with the updated "tmp" string.
Example
#include <bits/stdc++.h>
using namespace std;
int maxi = 0;
// Check for continuous characters in the substring
bool CheckForContinuous(string &tmp) {
// map to store the last index of the character
unordered_map<char, int> pos;
for (int p = 0; p < tmp.length(); p++) {
// When the last index exists in the map
if (pos[tmp[p]]) {
// If the last index is adjacent to the current index
if (p - pos[tmp[p]] + 1 <= 1)
pos[tmp[p]] = p + 1;
else
return false;
} else {
// When the map doesn't have a character as a key
pos[tmp[p]] = p + 1;
}
}
return true;
}
void getLongestSubSeq(string &alpha, string tmp, int start, int &k) {
// To store the character's frequency
unordered_map<char, int> f;
if (start == alpha.length()) {
if (tmp.length() > 0) {
// To store minimum and maximum frequency of characters
int minf = INT_MAX, maxf = INT_MIN;
// Make map empty
f.clear();
// Store frequency of characters in the map
for (int p = 0; p < tmp.length(); p++)
f[tmp[p]]++;
// Get minimum and maximum value from the map
for (auto &key : f) {
minf = min(minf, key.second);
maxf = max(maxf, key.second);
}
// Validate substring for frequency difference and continuous characters
if (maxf - minf <= k && CheckForContinuous(tmp))
maxi = max(maxi, (int)tmp.length());
}
return;
}
// Exclude current character
getLongestSubSeq(alpha, tmp, start + 1, k);
// Include current character
tmp.push_back(alpha[start]);
getLongestSubSeq(alpha, tmp, start + 1, k);
}
int main() {
string alpha = "ppppqrs", tmp;
int k = 2;
getLongestSubSeq(alpha, tmp, 0, k);
cout <<"The maximum length of the substring according to the given conditions is " << maxi;
return 0;
}
Output
The maximum length of the substring according to the given conditions is 6
Time complexity - O(N*2N), where O(N) is used to check consecutive characters and O(2N) is used to find all subsequences.
Space complexity - O(N) to store temporary subsequences.
We use a simple method to find all subsequences of a given string. However, this is very time consuming. It is not recommended to use this method to solve the problem with large strings.
The above is the detailed content of The longest subsequence whose characters are the same as the substring and whose frequency difference is at most K. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Which has a greater impact on performance, memory frequency or timing?
Feb 19, 2024 am 08:58 AM
Which has a greater impact on performance, memory frequency or timing?
Feb 19, 2024 am 08:58 AM
Memory is one of the most important components in the computer, and it has a significant impact on the performance and stability of the computer. When choosing memory, people tend to focus on two important parameters, namely timing and frequency. So, for memory performance, which is more important, timing or frequency? First, let's understand the concepts of timing and frequency. Timing refers to the time interval required for a memory chip to receive and process data. It is usually represented by a CL value (CASLatency). The smaller the CL value, the faster the memory processing speed. The frequency is within
 How to type arrows in Word
Apr 16, 2023 pm 11:37 PM
How to type arrows in Word
Apr 16, 2023 pm 11:37 PM
How to use AutoCorrect to type arrows in Word One of the fastest ways to type arrows in Word is to use the predefined AutoCorrect shortcuts. If you type a specific sequence of characters, Word automatically converts those characters into arrow symbols. You can draw many different arrow styles using this method. To type an arrow in Word using AutoCorrect: Move your cursor to the location in the document where you want the arrow to appear. Type one of the following character combinations: If you don't want what you type to be corrected to an arrow symbol, press the backspace key on your keyboard to
 How to apply superscript and subscript formatting options in Microsoft Excel
Apr 14, 2023 pm 12:07 PM
How to apply superscript and subscript formatting options in Microsoft Excel
Apr 14, 2023 pm 12:07 PM
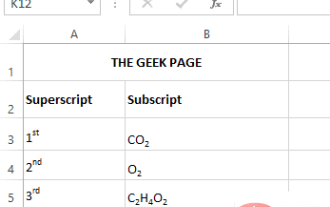
A superscript is a character or characters, either letters or numbers, that you need to set slightly above the normal line of text. For example, if you need to write 1st, the letter st needs to be slightly higher than the character 1. Likewise, a subscript is a group of characters or a single character and needs to be set slightly lower than normal text level. For example, when you write a chemical formula, you need to place the numbers below the normal line of characters. The following screenshots show some examples of superscript and subscript formatting. Although it may seem like a daunting task, applying superscript and subscript formatting to your text is actually quite simple. In this article, we will explain in some simple steps how to easily format text using superscript or subscript. Hope you enjoyed reading this article. How to apply superscript in Excel
 How do you enter extended characters, such as the degree symbol, on iPhone and Mac?
Apr 22, 2023 pm 02:01 PM
How do you enter extended characters, such as the degree symbol, on iPhone and Mac?
Apr 22, 2023 pm 02:01 PM
Your physical or numeric keyboard provides a limited number of character options on the surface. However, there are several ways to access accented letters, special characters, and more on iPhone, iPad, and Mac. The standard iOS keyboard gives you quick access to uppercase and lowercase letters, standard numbers, punctuation, and characters. Of course, there are many other characters. You can choose from letters with diacritics to upside-down question marks. You may have stumbled upon a hidden special character. If not, here's how to access them on iPhone, iPad, and Mac. How to Access Extended Characters on iPhone and iPad Getting extended characters on your iPhone or iPad is very simple. In "Information", "
 Use java's Character.isDigit() function to determine whether a character is a number
Jul 27, 2023 am 09:32 AM
Use java's Character.isDigit() function to determine whether a character is a number
Jul 27, 2023 am 09:32 AM
Use Java's Character.isDigit() function to determine whether a character is a numeric character. Characters are represented in the form of ASCII codes internally in the computer. Each character has a corresponding ASCII code. Among them, the ASCII code values corresponding to the numeric characters 0 to 9 are 48 to 57 respectively. To determine whether a character is a number, you can use the isDigit() method provided by the Character class in Java. The isDigit() method is of the Character class
 Correct way to display Chinese characters in matplotlib
Jan 13, 2024 am 11:03 AM
Correct way to display Chinese characters in matplotlib
Jan 13, 2024 am 11:03 AM
Correctly displaying Chinese characters in matplotlib is a problem often encountered by many Chinese users. By default, matplotlib uses English fonts and cannot display Chinese characters correctly. To solve this problem, we need to set the correct Chinese font and apply it to matplotlib. Below are some specific code examples to help you display Chinese characters correctly in matplotlib. First, we need to import the required libraries: importmatplot
 ASUS TUF Z790 Plus is compatible with ASUS MCP79 memory frequency
Jan 03, 2024 pm 04:18 PM
ASUS TUF Z790 Plus is compatible with ASUS MCP79 memory frequency
Jan 03, 2024 pm 04:18 PM
ASUS tufz790plus supports memory frequency. ASUS TUFZ790-PLUS motherboard is a high-performance motherboard that supports dual-channel DDR4 memory and supports up to 64GB of memory. Its memory frequency is very powerful, up to 4800MHz. Specific supported memory frequencies include 2133MHz, 2400MHz, 2666MHz, 2800MHz, 3000MHz, 3200MHz, 3600MHz, 3733MHz, 3866MHz, 4000MHz, 4133MHz, 4266MHz, 4400MHz, 4533MHz, 4600MHz, 4733MHz and 4800MHz. Whether it is daily use or high performance needs
 How to check the frequency of ddr4
Feb 01, 2024 am 09:42 AM
How to check the frequency of ddr4
Feb 01, 2024 am 09:42 AM
The biggest impact of ddr4 memory sticks on computers is frequency, and many users don't know how to check the frequency. In fact, you can check it through the CPU software, and all aspects of information are displayed in great detail. How to check the frequency of ddr4: 1. You must first check it through the software. You can use CPU-z to check it. 2. After it is done, open it and click "Memory". 3. At this time, you can see the "frequency" below.





