Calculate the maximum distance between two points on the coordinate plane using the rotating caliper method

In C, we have a predefined function sqrt which returns the square root of any number. The rotating caliper method is a technique used in solving algorithms or computational geometry.

Visual Representation of the Rotating Caliper Method

Hand Rotation shows a real-world example of a rotating caliper plot, showing the vertical orientation whenever the hand is rotated. We can also understand this concept by using polygons.

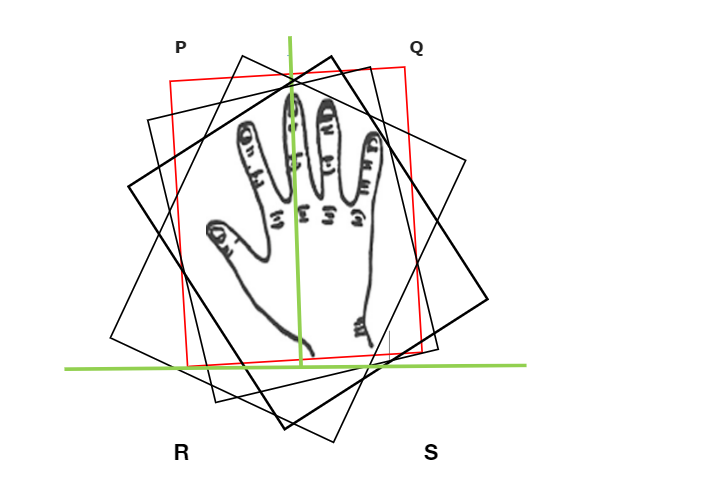
In this article, we will use the rotating caliper method to find the maximum distance between two coordinate points. 跨度>

grammar

Use the following syntax in the program -

vector<datatype> name

parameter

• Vectors - We start with keyword vectors and initialize the vectors in C.

• datatype - The type of data element represented by the vector.

• name - The name of the vector.

algorithm

• We will use the header files iostream, vector and cmath to start the program.

• We are creating a structure name point that will store the coordinates of x and y.

• We are defining a function definition of double data type distance() to calculate the distance between two coordinate points. Here, Points p1 and Point p2 are parameters that accept coordinate values ​​and return distance using predefined function sqrt and distance formula.

• We are defining a function definition called CP() whose double data type accepts parameters Point p1, Point p2 and Point p3 calculation Cross product vectors, i.e. p2-p1 and p3-p1 w.r.t x and y coordinates.

• Now we are creating a function definition of double precision data type rotatingCaliper() that takes the argument as a point vector and maximizes the distance between any two coordinate planes.

• We initialize the variable result to 0, which will be tracked to satisfy the calculation of the maximum distance. To find the size of the point, it will use a predefined function called size() and store it in the variable n.

• We initialize the two variables j and k to 1 and perform the following operations -

• We are moving j to the next point in the polygon and the cross product of the current edge 'points[i], points[CP i 1] % n'And the next edge 'points[j]' is less than the cross product CP of the current edge 'points[i]', points[ (i 1) % n]' and the edge after the next point 'point [(j 1) % n]'. This will verify that the current edge is perpendicular to the next edge.

• We move k to the next point in the polygon until the distance between the current point 'point[i]' and the next point ' The distance point[k]' is less than the distance between the current point 'point[i]' and the next point 'points[(k 1)%n]'. This will verify that the next point is furthest from the current point.

• Now we are calculating the distance between point j, k, and the current point 'point[i]', multiplying all these points, and then we Will get the maximum value in the result variable.

• We start the main function and apply the value of the coordinate plane to the "vector point" variable.

• Finally, we call the function name rotatingCaliper() and pass the 'points' value as parameter to get the maximum distance of the rotating caliper plot.

Example

In this program, we will use the rotating caliper method to perform the maximum distance between two points in the coordinate plane.

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
struct Point {
    double x, y;
};
// In this function we are calculating the distance between two coordinate point.
double distance(Point p1, Point p2) {
   return sqrt((p2.x - p1.x) * (p2.x - p1.x) + (p2.y - p1.y) * (p2.y - p1.y));
}
// In this function we are calculating the cross-product of two vector
double CP(Point p1, Point p2, Point p3) // CP: cross-product {
   return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
}
// In this function we are calculating the Rotating Caliper
double rotatingCalipers(vector<Point> points) {
   double result = 0;
  int n = points.size();
    int j = 1, k = 1;
   for (int i = 0; i < n; i++) {
       while (CP(points[i], points[(i + 1) % n], points[j]) < CP(points[i], points[(i + 1) % n], points[(j + 1) % n])) 
       {
           j = (j + 1) % n;
       }
       while (distance(points[i], points[k]) < distance(points[i], points[(k + 1) % n])) {
          k = (k + 1) % n;
       }
     // calculate the max distance
        result = max(result, distance(points[i], points[j]) * distance(points[i], points[k]));
   }
   return result;
}
int main() {
    vector<Point> points = {{0, 0}, {1, 1}, {1, 2}, {2, 2}, {2, 3}, {3, 3}, {3, 4}, {4, 4}, {4, 5}, {5, 5},{5,6}};
    cout << "Maximum distance between two coordinate points: "<<rotatingCalipers(points) << endl;
    return 0;
}

Output

Maximum distance between two coordinate points: 39.0512

in conclusion

We understand the concept of the rotating caliper method by calculating the maximum distance between two coordinate points. Practical applications of this method include aperture angle optimization, machine learning classification, etc.

The above is the detailed content of Calculate the maximum distance between two points on the coordinate plane using the rotating caliper method. For more information, please follow other related articles on the PHP Chinese website!