Backend Development
C++
What is the translation in C for the largest Ruhr triangle in a square inscribed in a circle?
What is the translation in C for the largest Ruhr triangle in a square inscribed in a circle?
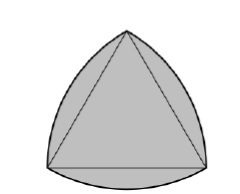
Roulet triangle is a shape formed by the intersection of three disks, with the center of each disk located on the boundary of the other two disks. Its boundary is a curve of constant width, which is the simplest and best-known curve besides the circle itself. Constant width means that every two parallel support lines are equally spaced apart, regardless of their orientation. Because its diameter is the same.
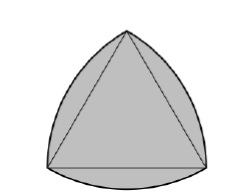
The boundaries of the Reuleaux triangle are curves of equal width based on the equilateral triangle. All points on a side are equidistant from the opposite vertex.
Constructing the Reuleaux triangle
Formula of the Reuleaux triangle
The area of the Reuleaux triangle if the curve is based on an equilateral triangle and the sides The triangle is h
A = (π * h<sup>2</sup>) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h<sup>2</sup> / 2 = 0.70477 * h<sup>2</sup>
The largest Reuleaux triangle within the square, inscribed in the circle
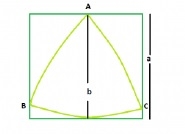
0.70477 * b2 where b is the distance between the parallel lines supporting the Reuleaux triangle.
The distance between the parallel lines supporting the Reuleaux triangle = the sides of the square, that is,a
The area of the Reuleaux triangle,A = 0.70477 * a2
Let’s give an example to better illustrate this concept,Input: r = 6 Output: 50.7434
a, then
a√2 = 2r
a = √2r
In the Reuleaux triangle,h = a = √2r,
The area triangle of Reuleaux triangle is,A = 0.70477*h^2 = 0.70477*2*r^2
Example#include <stdio.h>
#include<math.h>
int main() {
float r = 6;
float area = 0.70477 * 2 * pow(r, 2);
printf("The area is : %f",area);
return 0;
}Copy after login
Output#include <stdio.h>
#include<math.h>
int main() {
float r = 6;
float area = 0.70477 * 2 * pow(r, 2);
printf("The area is : %f",area);
return 0;
}The area is : 50.743439
Copy after login
The area is : 50.743439
The above is the detailed content of What is the translation in C for the largest Ruhr triangle in a square inscribed in a circle?. For more information, please follow other related articles on the PHP Chinese website!
Hot AI Tools
Undresser.AI Undress
AI-powered app for creating realistic nude photos
AI Clothes Remover
Online AI tool for removing clothes from photos.
Undress AI Tool
Undress images for free
Clothoff.io
AI clothes remover
AI Hentai Generator
Generate AI Hentai for free.
Hot Article
Hot Tools
Notepad++7.3.1
Easy-to-use and free code editor
SublimeText3 Chinese version
Chinese version, very easy to use
Zend Studio 13.0.1
Powerful PHP integrated development environment
Dreamweaver CS6
Visual web development tools
SublimeText3 Mac version
God-level code editing software (SublimeText3)
Hot Topics
1377
52
What is the largest square that can be inscribed in an equilateral triangle?
Sep 22, 2023 pm 06:21 PM
Here we will see the area of the largest square that can be inscribed in an equilateral triangle. The side length of the triangle is 'a' and the side length of the square is x. The side length 'a' of the triangle is − so x is − Example #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
Find the area of a circle inscribed in a square in Java
Aug 19, 2023 pm 04:53 PM
Acircleisaroundshapetwo-dimensionaldiagramwhichhasnocorners.Everycirclehasanoriginpointandeverypointonthecirclemaintainsequaldistancefromtheorigin.ThedistancebetweentheoriginandapointinacircleisknownasRadiusofthecircle.Andsimilarly,ifwedrawalinefromo
In a C program, translate the following into Chinese: What is the area of a square inscribed in a circle inscribed in an equilateral triangle?
Aug 31, 2023 pm 12:25 PM
Here we will see that the area of a square is inscribed in a circle, and that the circle is inscribed in an equilateral triangle. The side of the square is "a". The radius of the circle is "r" and the side of the hexagon is "A". The chart is shown below. So the diagonal of the square is - so the area of the square is - Example #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne
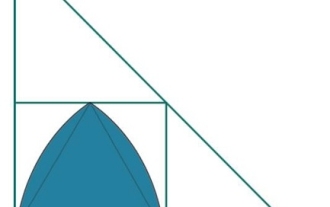What is the largest Ruero triangle inscribed in a square that is a right triangle?
Sep 04, 2023 pm 10:29 PM
Here we will see the area of the largest Reuleaux triangle inscribed in a square, which in turn is inscribed in a right triangle. The side length of the square is 'a'. The height of a Reuleaux triangle is x. The base of the triangle is b, the height is l, and the hypotenuse is h. We know that a square inscribed in a right triangle of height l and base b has side length - the height of a Reuleaux triangle is the same as a. So a=x. Therefore, the area of a Reuleaux triangle is - Example#include<iostream>#include<cmath>usingnamespacestd;fl
C program to calculate the area of a square within a circle inscribed in a hexagon
Aug 28, 2023 pm 08:41 PM
Given a square inscribed in a circle inscribed by a regular hexagon, we need to find the area of the square, and to do this we need to find the relationship between the side lengths of the square and the side lengths of the regular hexagon. The mathematical formula of the radius of the inscribed circle of a regular hexagon is, r=A√3/2. Since the diagonal of the square is equal to the diameter of the circle, the relationship between the radius and the side length is, a=√r according to the regular hexagon The side length of , a=√3A/√2, so, the area of the square, area=a2=(√3A/√2)2 Example #include<stdio.h>#inclu
In C, the largest Reuleaux triangle inside a square
Sep 07, 2023 pm 12:29 PM
A Lule triangle is a shape formed by the intersection of three disks, with the center of each disk on the boundary of the other two disks. Its boundary is a curve of constant width, and apart from the circle itself, it is the simplest and best-known such curve. Constant width means that the spacing between each two parallel support lines is the same, regardless of their orientation. Because all its diameters are the same. The boundaries of a Lule triangle are curves of constant width based on equilateral triangles. All points on an edge are equidistant from the opposite vertex. The formula for constructing a Lule triangle. If the curve is based on an equilateral triangle and the side length of the triangle is h, then the area of the Lule triangle is A=(π*h2)/2–2*(Areao
What is the area of a leaf within a square?
Aug 26, 2023 pm 05:13 PM
Here we will see how to calculate the area of a leaf-like object that lies within a square ABCD. Each side of the square has length 'a'. The leaf has two equal parts. The area of each part is p, now − the area of the whole leaf is 2p. Example #include<iostream>usingnamespacestd;floatleafArea(floata){ return(a*a*(3.1415/2-1));}intmain(){ floatsquare
Print maximum sum square submatrix of given size in C program
Sep 07, 2023 pm 01:53 PM
Given an NxN matrix, find a MxM submatrix with M=1 such that the sum of all elements of the matrix MxM is maximum. The input to the matrix NxN can contain zero, positive integer and negative integer values. Example Input: {{1,1,1,1,1}, {2,2,2,2,2}, {3,3,3,3,3}, {4,4,4,4,4 }, {5,5,5,5,5}}Output:&
