 Technology peripherals
Technology peripherals
 AI
AI
 GPT-4 explores global problems through 97 rounds of dialogue and reaches the conclusion that P≠NP
GPT-4 explores global problems through 97 rounds of dialogue and reaches the conclusion that P≠NP
GPT-4 explores global problems through 97 rounds of dialogue and reaches the conclusion that P≠NP
For those who are in the field of scientific research, they have more or less heard of the P/NP problem. This problem was included in the Millennium Prize problem by the Clay Mathematics Institute. There are seven problems in it. Big problems, including the well-known Poincaré conjecture, Riemann hypothesis, etc. And the organization has offered millions of dollars in prizes to researchers who can solve the problem.
The P/NP problem was first proposed in 1971 by Stephen A. Cook and Leonid Levin respectively. Over the years, many people have devoted themselves to researching this problem. However, some people say that it may take a conservative estimate of 100 years to solve the P=NP problem
In recent years, some people have claimed to have proved that P is equal to or not equal to NP, but these There are errors in the proof process. However, so far, no one has been able to give a definite answer
With the development of artificial intelligence technology, especially the rapid update of large language models in the past year, researchers Begin to try to use artificial intelligence technology to solve some global problems
Researchers from Microsoft Research, Peking University, Beihang University and other institutions proposed to use large language models (LLM) to enhance and accelerating the research on P versus NP problems
This article proposes a general framework, Socratic reasoning, to prompt LLM to think deeply and solve complex problems. On the basis of this framework, LLM is able to recursively discover, solve and integrate problems, while also conducting self-evaluation and improvement
This paper's pilot study on the P vs. NP problem shows that, GPT-4 successfully generated a proof pattern and conducted rigorous reasoning in 97 dialogue rounds, reaching the conclusion that "P≠ NP", which is consistent with the conclusion of (Xu and Zhou, 2023).

Please click the following link to view the paper: https://arxiv.org/pdf/2309.05689.pdf
The main contributions of this article can be summarized as follows:
- ## Use LLM as a collaborative partner with humans to address complex scientific challenges, and propose "LLM for Science (LLM4Science )" paradigm.
- Introduces a framework called "Socratic Reasoning" to encourage LLM to use deduction, transformation, decomposition and other modes to stimulate critical thinking.
- Conduct a pilot study using GPT-4 and the Socratic reasoning framework to solve P versus NP problems in theoretical computer science.
- GPT-4 successfully generated proof patterns and conducted rigorous reasoning in 97 dialogue turns, reaching the conclusion that P ≠ NP, consistent with Xu and Zhou (2023 ) recent work consistent.
- This research demonstrates the potential ability of LLMs like GPT-4 to infer new knowledge and explore complex expert-level problems in collaboration with humans.
- This article highlights LLM as a general innovation leader across domains, unlike previous specialized AI models tailored for specific tasks.
- LLM The ability to use natural and mathematical language fluently is essential for interdisciplinary discovery.
- This work reveals how LLM can be leveraged as a partner to enhance and accelerate the scientific research process across diverse fields.
Rewritten content: This paragraph mentions that they named the framework "Socratic Reasoning" after being inspired by the ancient Greek philosopher Socrates. . Socrates once said: "I can teach no one anything. I can only make them think." And the overall design idea of the framework is the same. It is a general problem-solving framework that allows LLM to be used in a wide range of Navigate the solution space and arrive at answers effectively
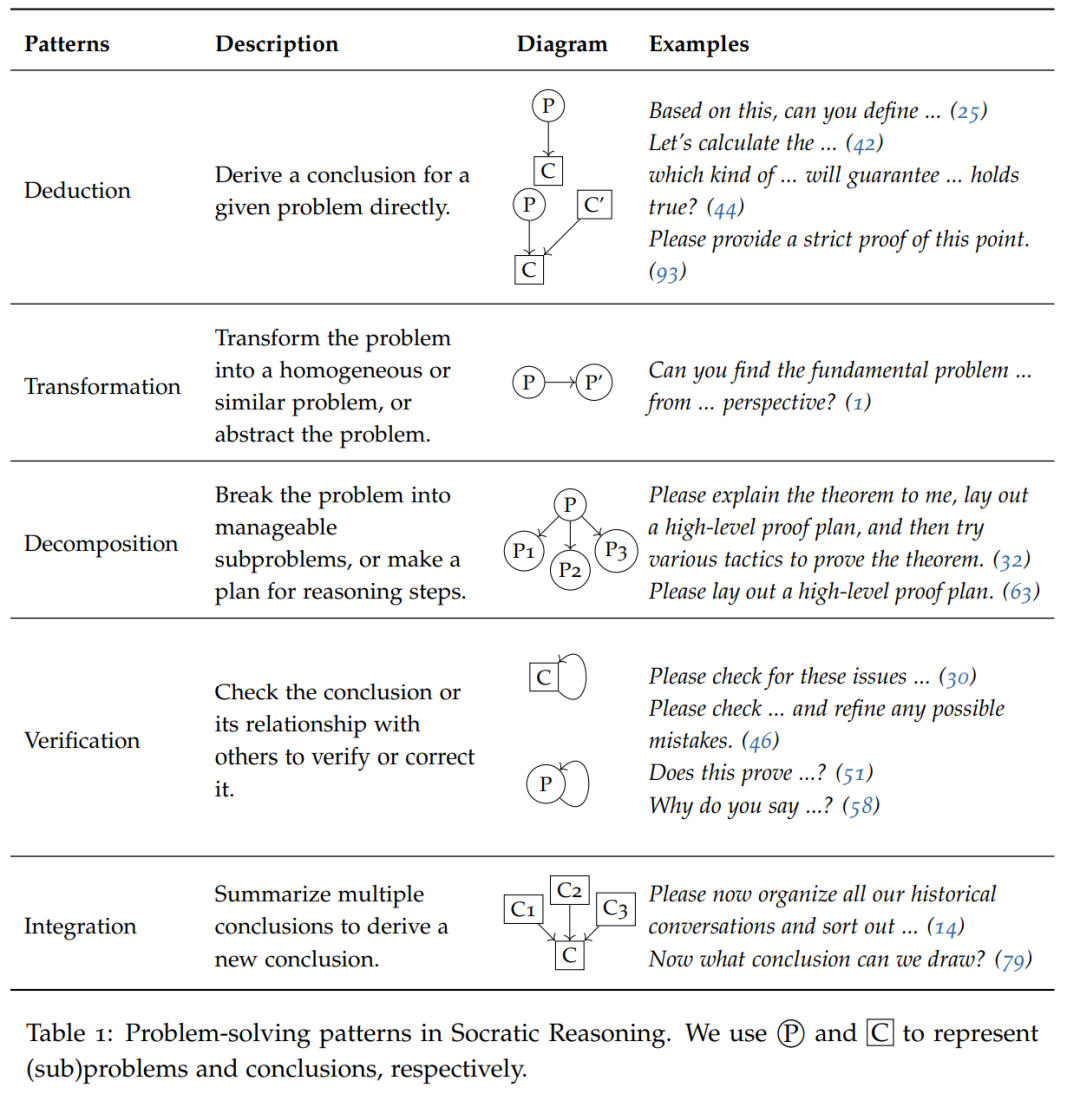
Table 1 lists the five prompt modes of "Socratic Reasoning": deduction, transformation, decomposition, verification and fusion. These patterns are used to discover new insights and perspectives, break complex problems into sub-questions or small steps, and engage in self-improvement by challenging responses to answers
in smaller problems ( atomic problem), LLM can directly give inference results. At this time, the deductive mode (for example, the prompt is let us think step by step...) is used to guide LLM to directly draw conclusions.
For more complex problems, this article first requires LLM to transform the problem into a new problem or decompose it into several sub-problems. These patterns are then executed recursively until the atomic ji problem is reached.
When new problems arise or new conclusions are drawn, verification mode should be adopted and LLM’s self-assessment capabilities should be used to verify and improve
Finally, the fusion mode requires the LLM to synthesize conclusions based on the results of the sub-problems
recursively motivates the LLM through a series of dialogues to continue the above process until the target problem is solved
In this work, "Socratic Reasoning" provides a systematic prompt framework for challenging questions
The picture below is an example of a dialogue used to solve the P vs. NP problem in "Socratic Reasoning". The GPT-4 API is used in the case study, and in addition, the article sorts the processes based on round index.

In the process of exploration, this article introduces five different roles as auxiliary provers, such as mathematicians who are proficient in probability theory. A total of 97 rounds of dialogue were conducted in the experiment, divided into 14 rounds before and 83 rounds after.
For example, the first round prompt: You can talk from a philosophical perspective rather than from a computer theory From the perspective of P!=NP, can we find the fundamental problem behind P!=NP?

Here are other tips:


The dialogue continues, and the final round of dialogue is as follows: Finally, it is concluded that P≠ NP

Interested readers can Check out the original paper to learn more.
The above is the detailed content of GPT-4 explores global problems through 97 rounds of dialogue and reaches the conclusion that P≠NP. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1359
1359
 52
52
 How to correctly display the locally installed 'Jingnan Mai Round Body' on the web page?
Apr 05, 2025 pm 10:33 PM
How to correctly display the locally installed 'Jingnan Mai Round Body' on the web page?
Apr 05, 2025 pm 10:33 PM
Using locally installed font files in web pages Recently, I downloaded a free font from the internet and successfully installed it into my system. Now...
 Does H5 page production require continuous maintenance?
Apr 05, 2025 pm 11:27 PM
Does H5 page production require continuous maintenance?
Apr 05, 2025 pm 11:27 PM
The H5 page needs to be maintained continuously, because of factors such as code vulnerabilities, browser compatibility, performance optimization, security updates and user experience improvements. Effective maintenance methods include establishing a complete testing system, using version control tools, regularly monitoring page performance, collecting user feedback and formulating maintenance plans.
 Where to get the material for H5 page production
Apr 05, 2025 pm 11:33 PM
Where to get the material for H5 page production
Apr 05, 2025 pm 11:33 PM
The main sources of H5 page materials are: 1. Professional material website (paid, high quality, clear copyright); 2. Homemade material (high uniqueness, but time-consuming); 3. Open source material library (free, need to be carefully screened); 4. Picture/video website (copyright verified is required). In addition, unified material style, size adaptation, compression processing, and copyright protection are key points that need to be paid attention to.
 How to select a child element with the first class name item through CSS?
Apr 05, 2025 pm 11:24 PM
How to select a child element with the first class name item through CSS?
Apr 05, 2025 pm 11:24 PM
When the number of elements is not fixed, how to select the first child element of the specified class name through CSS. When processing HTML structure, you often encounter different elements...
 Why does negative margins not take effect in some cases? How to solve this problem?
Apr 05, 2025 pm 10:18 PM
Why does negative margins not take effect in some cases? How to solve this problem?
Apr 05, 2025 pm 10:18 PM
Why do negative margins not take effect in some cases? During programming, negative margins in CSS (negative...
 What application scenarios are suitable for H5 page production
Apr 05, 2025 pm 11:36 PM
What application scenarios are suitable for H5 page production
Apr 05, 2025 pm 11:36 PM
H5 (HTML5) is suitable for lightweight applications, such as marketing campaign pages, product display pages and corporate promotion micro-websites. Its advantages lie in cross-platformity and rich interactivity, but its limitations lie in complex interactions and animations, local resource access and offline capabilities.
 How to use the shape-outside attribute of CSS to achieve the display effect of gradually shortening text?
Apr 05, 2025 pm 10:54 PM
How to use the shape-outside attribute of CSS to achieve the display effect of gradually shortening text?
Apr 05, 2025 pm 10:54 PM
Implementing the display effect of gradually shortening text In web design, how to achieve a special text display effect to make the text length gradually shortening? This effect...
 How to solve the problem of loading when PS is started?
Apr 06, 2025 pm 06:36 PM
How to solve the problem of loading when PS is started?
Apr 06, 2025 pm 06:36 PM
A PS stuck on "Loading" when booting can be caused by various reasons: Disable corrupt or conflicting plugins. Delete or rename a corrupted configuration file. Close unnecessary programs or upgrade memory to avoid insufficient memory. Upgrade to a solid-state drive to speed up hard drive reading. Reinstalling PS to repair corrupt system files or installation package issues. View error information during the startup process of error log analysis.



