Add all larger values in the given binary search tree to each node
Here we will see an interesting problem, we will add a larger value to each node in a given binary search tree. So the initial and final tree will look like this -
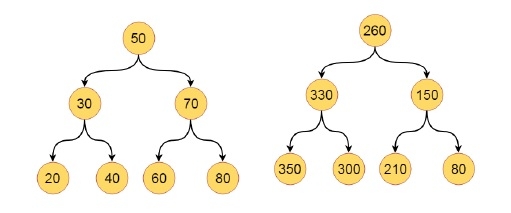
Begin if root is null, then stop bstUpdate(right of room, sum) sum := sum + value of root update root value using sum bstUpdate(left of room, sum) End
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}Copy after login
Output#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}350 330 300 260 210 150 80
Copy after login
350 330 300 260 210 150 80
The above is the detailed content of Add all larger values in the given binary search tree to each node. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 C++ code to reverse paths in a binary search tree using queues
Sep 14, 2023 pm 07:21 PM
C++ code to reverse paths in a binary search tree using queues
Sep 14, 2023 pm 07:21 PM
For example, given a binary search tree, we need to reverse its path from a specific key. Ways to find the solution In this approach we will create a queue and push all the nodes until we get the root node. p>Example #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey; structnode*left,*right;};structnode*newNode(intitem){&nb
 How to implement a binary search tree in Python
Jun 10, 2023 am 08:57 AM
How to implement a binary search tree in Python
Jun 10, 2023 am 08:57 AM
Binary Search Tree (BinarySearchTree, BST) is a search algorithm based on binary trees. Its characteristic is that the value in the left subtree of each node in the tree is smaller than the value of this node, while the value in the right subtree is greater than the value of this node. Therefore, the time complexity of BST search and insertion operations is O(logN). The method of implementing a binary search tree in Python is relatively simple, because Python has two built-in data structures, lists and dictionaries, both of which can be used to implement binary trees. At this
 Binary heap and binary search tree in C++
Aug 22, 2023 pm 04:10 PM
Binary heap and binary search tree in C++
Aug 22, 2023 pm 04:10 PM
In C++ programming, binary heap and binary search tree are two commonly used data structures. They have similarities, but they also have differences. This article will introduce the concepts, basic operations and application scenarios of binary heaps and binary search trees respectively. 1. Binary Heap 1.1 Concept Binary heap is a complete binary tree that satisfies the following two properties: 1.1.1 Heap ordering Heap ordering means that in a binary heap, the value of each node is not greater than (or not less than) the value of its parent node. Here we take the maximum heap as an example, that is, the value of the root node is the largest value in the entire tree, and
 Java uses the max() function of the Math class to obtain the larger of two numbers
Jul 24, 2023 pm 11:17 PM
Java uses the max() function of the Math class to obtain the larger of two numbers
Jul 24, 2023 pm 11:17 PM
Java uses the max() function of the Math class to obtain the larger value of two numbers. In Java programming, we often need to compare the sizes of two numbers and then select the larger number to perform some operations. The Math class in Java provides many functions for mathematical operations, among which the max() function can help us obtain the larger value of two numbers. The Math.max() function is defined as follows: publicstaticintmax(inta,intb) This function accepts two integers
 How to write a binary search tree algorithm using C#
Sep 19, 2023 pm 01:03 PM
How to write a binary search tree algorithm using C#
Sep 19, 2023 pm 01:03 PM
How to use C# to write a binary search tree algorithm requires specific code examples. Binary Search Tree (BinarySearchTree, referred to as BST) is a commonly used data structure that has the characteristics of fast insertion, search, and deletion operations. In C#, we can use object-oriented approach to write binary search tree algorithm. First, we need to define a class for a binary search tree node that contains a value and two pointers to the left and right child nodes. The code looks like this: publicclassBST
 How to implement binary search tree algorithm using java
Sep 19, 2023 am 08:48 AM
How to implement binary search tree algorithm using java
Sep 19, 2023 am 08:48 AM
How to use Java to implement the binary search tree algorithm Binary Search Tree (BinarySearchTree, BST for short) is a commonly used data structure that can efficiently implement operations such as insertion, deletion, and search. This article will introduce how to use Java to implement a binary search tree and provide corresponding code examples. 1. Definition of Binary Search Tree A binary search tree is an ordered tree with the following characteristics: Each node has a unique key value. The key value of the left subtree is less than the key value of the node, and the key value of the right subtree is greater than the key value of the node.
 Add all larger values in the given binary search tree to each node
Sep 16, 2023 pm 08:45 PM
Add all larger values in the given binary search tree to each node
Sep 16, 2023 pm 08:45 PM
Here we will see an interesting problem, we will add a larger value to each node in a given binary search tree. Therefore, the initial and final trees will look like this - Algorithm bstUpdate(root,sum)-Begin ifrootisnull,thenstop bstUpdate(rightofroom,sum) sum:=sum+valueofroot updaterootvalueus
 Add all larger values in the given binary search tree to each node
Sep 07, 2023 pm 12:17 PM
Add all larger values in the given binary search tree to each node
Sep 07, 2023 pm 12:17 PM
BST or Binary Search Tree is a form of binary tree in which all left nodes have values less than the value of the root node and all right nodes have values greater than the value of the root node. For this problem, we will take a binary tree and add to it all values greater than the current node value. The problem "add all larger values to each node of a BST" is simplified to, for a BST, add all node values larger than the current node value to that node value. Add all larger value nodes to each node in BST Problem Statement: Given a Binary Search Tree (BST), we need to add for each node the sum of all larger value nodes. Enter 10 /&nb






