Java program to find the area of a square using method overloading

We can use method overloading to calculate the area of a square in Java. "Method overloading" is a feature in Java that allows people to write multiple method names in the same class using the same method name. It will allow us to declare multiple methods with the same name but with different signatures, i.e. the number of parameters in the methods may be different or the data types of the parameters may be different. Method overloading helps us increase the readability of our code so that we can use the same method in different ways.
Now, let us take "Area of a Square" as an example to implement method overloading in Java.
Area of a square
The area of a square is the defined area it occupies on a two-dimensional plane. We can calculate the area of a square by multiplying the side length * side length.
Area of Square = s*s where s: side of square
In the following example, we will take the area of a square as an example and implement method overloading in Java by changing the data type of the parameter.
algorithm
Step 1 - Write a custom class to find the area of a square.
STEP 2 - Initialize a pair of two variables of different data types in the main method of the public class.
Step 3 - Create an object of the custom class in the main method of the public class.
Step 4 − Call a specific method to find the area of the square using the custom object you created.
The Chinese translation ofExample
is:Example
In this example, we calculate the area of a square using basic formulas and implement method overloading in Java.
Method overloading is achieved by changing the parameter type in the "areaOfSquare" method. Now, when the user inputs a parameter value of integer type to the areaOfSquare method, the first areaOfSquare method of the Area class is called and outputs the result. If the user enters a parameter of double type, the second areaOfSquare method is called and executed.
//Java Code to achieve Method Overloading in Java by Area of Square.
import java.io.*;
class Area {
// In this example area method is overloaded by changing the type of parameters.
public void areaOfSquare(int side) {
int area = 0;
area = side * side;
System.out.println("Area of the square is :" + area);
}
public void areaOfSquare(double side) {
double area= 0;
area = side*side;
System.out.println("Area of the square is:" + area);
}
}
public class Main {
public static void main(String args[]) {
Area Object = new Area();
int side_1= 3;
Object.areaOfSquare(side_1);
double side_2 = 4.5;
Object.areaOfSquare(side_2);
}
}
Output
Area of the square is :9 Area of the square is:20.25
Time complexity: O(1) Auxiliary space: O(1)
The Chinese translation ofExample
is:Example
In this example, we use the Math.pow() function to calculate the area of a square and implement method overloading in Java.
Method overloading is achieved by changing the parameter type in the "areaOfSquare" method. Now, when the user inputs a parameter value of integer type to the areaOfSquare method, the first areaOfSquare method of the Area class is called and outputs the result. If the user enters a parameter of double type, the second areaOfSquare method is called and executed.
//Java Code to achieve Method Overloading in Java by Area of Square.
import java.io.*;
class Area {
// In this example area method is overloaded by changing the type of parameters.
public void areaOfSquare(int side) {
int area = 0;
area =(int) Math.pow(side,2);
System.out.println("Area of the square is :" + area);
}
public void areaOfSquare(double side) {
double area= 0;
area = Math.pow(side,2);
System.out.println("Area of the square is:" + area);
}
}
public class Main {
public static void main(String args[]) {
Area Object = new Area();
int side_1= 3;
Object.areaOfSquare(side_1);
double side_2 = 4.5;
Object.areaOfSquare(side_2);
}
}
Output
Area of the square is :9 Area of the square is:20.25
Time complexity: O(1) Auxiliary space: O(1)
So, in this article, we take finding the area of a square as an example and learn how to implement method overloading in Java by changing the data type of the parameter.
The above is the detailed content of Java program to find the area of a square using method overloading. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
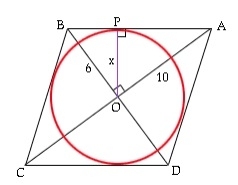 What is the area of a circle inscribed in a rhombus?
Sep 05, 2023 am 08:25 AM
What is the area of a circle inscribed in a rhombus?
Sep 05, 2023 am 08:25 AM
The inscribed circle of a rhombus is tangent to its four sides and four endpoints. The sides of the rhombus are tangent to the circle. Here, r is the radius found using a and the diagonal of the given value. Now the area triangle AOB = ½*OA*OB = ½*AB*r (both using the formula ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Circle area = π*r*r=π*(a2*b2)/4(a2support>+b2) Example of the diagonals of rhombus 5 and 10. Area is 15.700000 Example code Real-time demonstration #include<stdio.h>intma
 How to mark the area in CAD
Mar 14, 2023 am 11:30 AM
How to mark the area in CAD
Mar 14, 2023 am 11:30 AM
Method for area labeling in CAD: 1. Open CAD, click "Draw" to draw graphics; 2. Enter the "AREA" command and press Enter; 3. Select the area; 4. Press the space bar to display the area of the area; 5. Enter the command "T" and then enter the size of the area within the area.
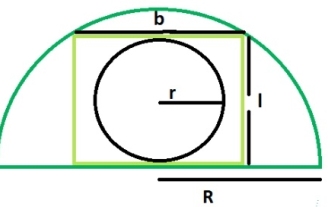 What is the area of a circle within a rectangle inscribed in a semicircle?
Sep 13, 2023 am 08:45 AM
What is the area of a circle within a rectangle inscribed in a semicircle?
Sep 13, 2023 am 08:45 AM
A circle inscribed in a rectangle is tangent to the longer side of the rectangle, that is, its length is tangent to the circle. A rectangle inscribed in a semicircle touches two points on the arc of the semicircle. The width of the rectangle is equal to the diameter of the circle. If R is the radius of the semicircle. The length of the rectangle = √2R/2 The width of the rectangle = R/√2 The radius of the inscribed circle is r = b/2 = R/2√2 Using this formula we can calculate the rectangle inscribed in the semicircle The area of a circle, area = (π*r2)=π*R/8 Example Demonstration #include<stdio.h>intmain(){&
 What is the area of the circular sector?
Aug 30, 2023 am 08:33 AM
What is the area of the circular sector?
Aug 30, 2023 am 08:33 AM
A circular sector, also known as a circular sector/sector of a circle, is a portion of a circle bounded by an arc between two radii. This area is bounded by two radii and an arc. To find the area inscribed, we need to find the angle between the two radii. The total area is equal to 360 degrees of angle. To find the area of an angle, we multiply the area by θ/360. This gives the area of the inscribed part. where θ is the angle (in degrees) between the two radii. The area of the circular sector = π*r*r*(θ/360). For example, the area of a circular sector with a radius of 5 and an angle of 60 degrees is 13.083. Area=(3.14*5*5)*(60/360)=13.03Example codeDemo#incl
 Why does Go language not support the design concept of method overloading?
Apr 04, 2024 am 09:00 AM
Why does Go language not support the design concept of method overloading?
Apr 04, 2024 am 09:00 AM
The Go language does not support method overloading because its design philosophy emphasizes simplicity, concurrency, and type safety. Method overloading can introduce name conflicts, complex type systems, and code confusion. To compensate for this, the Go language provides functions that allow the creation of functions with the same name but different parameter types in the same package, similar to the functionality of method overloading.
 How to measure the area of graphics in CAD Viewer. How to measure the area of graphics in CAD Viewer.
Mar 13, 2024 pm 01:43 PM
How to measure the area of graphics in CAD Viewer. How to measure the area of graphics in CAD Viewer.
Mar 13, 2024 pm 01:43 PM
How to measure the area of graphics in CAD Viewer? CAD Viewer is a very easy-to-use software for viewing engineering drawings. This software has many functions, and drawings in various formats can be opened and viewed. If when we look at the drawings, we find that the area measurement of some graphics is wrong or that some graphics forget to measure the area, we can use this software to measure the area of the graphics. So how to measure the area of graphics? Below, the editor of this site has compiled a CAD drawing king's steps to measure the area of graphics for your reference. Steps for measuring the graphic area in CAD Viewer 1. First, open the drawing file in CAD Viewer APP, take the drawing with arc graphics as an example, and measure the area of the graphic. 2. After opening the drawing, go to the bottom of the software interface
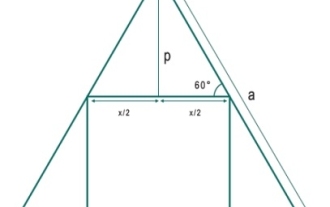 What is the largest square that can be inscribed in an equilateral triangle?
Sep 22, 2023 pm 06:21 PM
What is the largest square that can be inscribed in an equilateral triangle?
Sep 22, 2023 pm 06:21 PM
Here we will see the area of the largest square that can be inscribed in an equilateral triangle. The side length of the triangle is 'a' and the side length of the square is x. The side length 'a' of the triangle is − so x is − Example #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
 Find the area of a circle inscribed in a square in Java
Aug 19, 2023 pm 04:53 PM
Find the area of a circle inscribed in a square in Java
Aug 19, 2023 pm 04:53 PM
Acircleisaroundshapetwo-dimensionaldiagramwhichhasnocorners.Everycirclehasanoriginpointandeverypointonthecirclemaintainsequaldistancefromtheorigin.ThedistancebetweentheoriginandapointinacircleisknownasRadiusofthecircle.Andsimilarly,ifwedrawalinefromo




