C/C++ program written using merge sort algorithm to calculate reverse logarithm in an array?

The reversal count that occurs when sorting a given array is called reversal counting. The inverse problem is a classic problem that can be solved using the merge sort algorithm. In this problem v we will count all elements to its left that are greater than it and add the count to the output. This logic is completed in the merge function of merge sort.

To understand this topic better, let us take an example. Let us consider the two sub-arrays involved in the merge process -

##

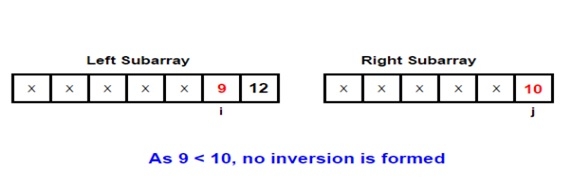
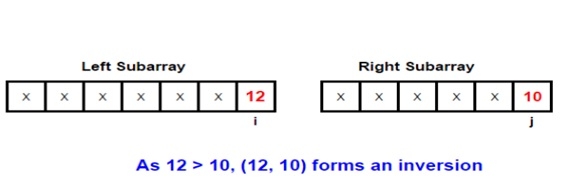
Input: arr[] = { 1, 9, 6, 4, 5}
Output: Inversion count is 5

Explanation

The number of reversals of the array

Given an array, find the number of reversals. If (i < j) and (A[i] > A[j]) then the pair (i, j) is called the inversion of the array A. We need to count all such pairs in arr

For example, < p>

There are 5 inversions in the array

(9,6), (9,4), (9,5), (6,4), (6,5)

1. Compare the values ​​of elements with each other.

2. If the value at the lower index is higher, increment the counter.

3. Display the results.

Example

#include <stdio.h>
int Merge(int arr[], int aux[], int low, int mid, int high) {
   int k = low, i = low, j = mid + 1;
   int inversionCount = 0;
   while (i <= mid && j <= high) {
      if (arr[i] <= arr[j]) {
         aux[k++] = arr[i++];
      } else {
         aux[k++] = arr[j++];
         inversionCount += (mid - i + 1); // NOTE
      }
   }
   while (i <= mid)
   aux[k++] = arr[i++];
   for (int i = low; i <= high; i++)
      arr[i] = aux[i];
   return inversionCount;
}
int MergeSort(int arr[], int aux[], int low, int high) {
   if (high == low) // if run size == 1
      return 0;
   int mid = (low + ((high - low) >> 1));
   int inversionCount = 0;
   inversionCount += MergeSort(arr, aux, low, mid);
   inversionCount += MergeSort(arr, aux, mid + 1, high);
   inversionCount += Merge(arr, aux, low, mid, high);
   return inversionCount;
}
int main() {
   int arr[] = { 1, 9, 6, 4, 5 };
   int N = 5;
   int aux[N];
   for (int i = 0; i < N; i++)
      aux[i] = arr[i];
   printf("Inversion count is %d", MergeSort(arr, aux, 0, N - 1));
   return 0;
}

The above is the detailed content of C/C++ program written using merge sort algorithm to calculate reverse logarithm in an array?. For more information, please follow other related articles on the PHP Chinese website!