
A dominant set of a graph is an NP-complete problem, which is a subset of vertices such that every vertex or adjacent vertex in the subset is in the subset. The full form of NP is "non-deterministic polynomial" which will check the problem in polynomial time, meaning we can check in polynomial time whether the solution is correct. Polynomial time has the best performance for codes like linear search time complexity – n, binary search – logn, merge sort – n(log)n etc. Complexity. NP-complete graphs provide a good solution in reasonable time. This application is used in areas such as network control, topology creation in computer laboratories, social networks and distributed computing.
Let us understand and check if a node has the dominant set of a NP complete graph.
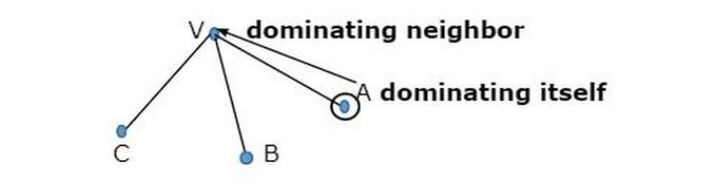
A vertex is said to dominate itself and each of its neighbors.
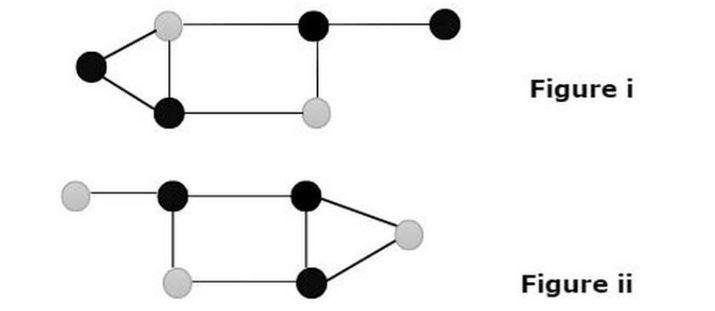
We see two graphs showing that the gray color of the nodes in the graph is dominant in nature.
G = V, E
parameter
G is considered a graph, V is considered a vertex, and E is considered an edge.
Given a graph G(V, E) and an integer k, determine whether the graph has a dominating set of size k. An input specified as a problem is considered an instance of the problem. The graph G(V, E) and the integer k serve as examples of the dominating set problem, which asks whether the graph G can have a dominating set in G. Since the definition of an NP-complete problem is a problem that is both NP and NP-hard, proving that a problem is NP-complete has two components −
If there is an NP problem Y that can be reduced to X in polynomial time, then X is an NP-complete problem. NP-complete problems are just as hard as NP problems. A problem is NP-Complete if it is part both an NP problem and an NP-Hard problem. Nondeterministic Turing machines can solve NP-complete problems in polynomial time. When a problem is np-complete, it has both np and np-hard combinations.
This means that problems with np solutions can be verified in polynomial time.
Real examples that are NP-complete have dominating sets, such as -
Decision-making problem.
The graphics are consistent.
NP_search( key ) {
arraylist[100];
i = array_check(key);
if(list[i]==key) {
searching found at index i.
} else {
searching found at index i.
}
}
Therefore, the total time complexity of this algorithm is O(1), but we do not know which search technique is more useful for solving this problem, which is called a non-deterministic algorithm.
If there is an NP-complete problem Y that can be reduced to problem X in polynomial time, then problem X is NP-hard. NP-hard problems are as hard as NP-complete problems. An NP-hard problem does not necessarily belong to the NP category.
If every NP problem can be solved in polynomial time, it is called NP-Hard. Many times, a specific problem is used to solve and reduce other problems.
Real examples of NP-hard have dominating sets such as -
Hamiltonian circuit
Optimization
Shortest route
We learned the concept that the dominant set of a graph is NP-complete. We see how discrete mathematics is an important aspect connecting these problems, such as Hamilton cycles, shortest paths, etc. In programming terms, NP-complete problems are a class of problems that are difficult to find but whose solutions can be directly verified in polynomial time.
The above is the detailed content of Prove that the dominant set of a graph is NP-complete. For more information, please follow other related articles on the PHP Chinese website!
 windows10 installation failed
windows10 installation failed
 How to set linux environment variables
How to set linux environment variables
 How to leave two spaces empty in a paragraph in html
How to leave two spaces empty in a paragraph in html
 There is no network adapter in device manager
There is no network adapter in device manager
 Laptop sound card driver
Laptop sound card driver
 Detailed explanation of onbeforeunload event
Detailed explanation of onbeforeunload event
 What are the commonly used shortcut keys in WPS?
What are the commonly used shortcut keys in WPS?
 How to set automatic line wrapping in word
How to set automatic line wrapping in word