 Backend Development
Backend Development
 PHP Tutorial
PHP Tutorial
 How to solve the minimum spanning tree problem in PHP using the divide-and-conquer method and obtain the optimal solution?
How to solve the minimum spanning tree problem in PHP using the divide-and-conquer method and obtain the optimal solution?
How to solve the minimum spanning tree problem in PHP using the divide-and-conquer method and obtain the optimal solution?

How to use the divide-and-conquer method to solve the minimum spanning tree problem in PHP and obtain the optimal solution?
Minimum spanning tree is a classic problem in graph theory, which aims to find a subset of all vertices in a connected graph, and connect the edges so that the subset forms a tree, and the weights of all edges The sum is the smallest. The divide-and-conquer method is an idea of decomposing a large problem into multiple sub-problems, then solving the sub-problems one by one and finally merging the results. Using the divide-and-conquer method to solve the minimum spanning tree problem in PHP can be achieved by following the following steps.
- Define the data structure of the graph:
First, we need to define the data structure of the graph. Graphs can be represented using arrays and two-dimensional arrays, where arrays represent vertices and two-dimensional arrays represent edges. Other attributes such as weights can be added according to actual needs.
class Graph {
public $vertices;
public $edges;
public function __construct($vertices) {
$this->vertices = $vertices;
$this->edges = array();
}
public function addEdge($u, $v, $weight) {
$this->edges[] = array("u" => $u, "v" => $v, "weight" => $weight);
}
}- Implement the divide-and-conquer algorithm to solve the minimum spanning tree:
Next, we need to implement the divide-and-conquer algorithm to solve the minimum spanning tree. The specific steps are as follows:
- Basic situation: If the graph has only one vertex, return that vertex.
- Decomposition steps: Divide the graph into two subgraphs.
- Recursive solution: Recursively call the minimum spanning tree algorithm for each subgraph.
- Merge result: merge the minimum spanning trees of the two subgraphs into one.
The following is a code example to solve the minimum spanning tree using the divide-and-conquer method:
function minSpanningTree($graph) {
// 基准情况:图只有一个顶点
if ($graph->vertices == 1) {
return array();
}
// 选择两个子图
$subgraph1 = new Graph($graph->vertices / 2);
$subgraph2 = new Graph($graph->vertices - $graph->vertices / 2);
// 将边分配给子图
foreach ($graph->edges as $edge) {
if ($edge["v"] <= $graph->vertices / 2) {
$subgraph1->addEdge($edge["u"], $edge["v"], $edge["weight"]);
} else {
$subgraph2->addEdge($edge["u"], $edge["v"] - $graph->vertices / 2, $edge["weight"]);
}
}
// 递归求解子图的最小生成树
$tree1 = minSpanningTree($subgraph1);
$tree2 = minSpanningTree($subgraph2);
// 合并两个子图的最小生成树
$tree = array_merge($tree1, $tree2);
// 返回最小生成树
return $tree;
}- Testing and application:
Finally, we can Use the above algorithm to solve the minimum spanning tree problem and obtain the optimal solution. The following is a simple test example:
// 创建一个带权重的无向图
$graph = new Graph(4);
$graph->addEdge(1, 2, 1);
$graph->addEdge(1, 3, 2);
$graph->addEdge(2, 3, 3);
$graph->addEdge(2, 4, 4);
$graph->addEdge(3, 4, 5);
// 求解最小生成树
$tree = minSpanningTree($graph);
// 输出最小生成树的边和权重
foreach ($tree as $edge) {
echo $edge["u"] . "-" . $edge["v"] . " weight: " . $edge["weight"] . "
";
}Running the above code will output the following results:
1-2 weight: 1 2-3 weight: 3 3-4 weight: 5
As you can see, using the divide-and-conquer method to solve the minimum spanning tree problem, we successfully obtained Minimum spanning tree of the graph, and the optimal solution is obtained.
The above is the detailed content of How to solve the minimum spanning tree problem in PHP using the divide-and-conquer method and obtain the optimal solution?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 CakePHP Project Configuration
Sep 10, 2024 pm 05:25 PM
CakePHP Project Configuration
Sep 10, 2024 pm 05:25 PM
In this chapter, we will understand the Environment Variables, General Configuration, Database Configuration and Email Configuration in CakePHP.
 PHP 8.4 Installation and Upgrade guide for Ubuntu and Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 Installation and Upgrade guide for Ubuntu and Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 brings several new features, security improvements, and performance improvements with healthy amounts of feature deprecations and removals. This guide explains how to install PHP 8.4 or upgrade to PHP 8.4 on Ubuntu, Debian, or their derivati
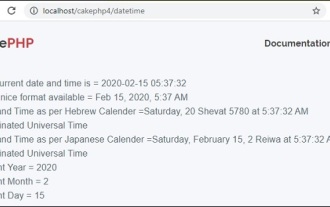 CakePHP Date and Time
Sep 10, 2024 pm 05:27 PM
CakePHP Date and Time
Sep 10, 2024 pm 05:27 PM
To work with date and time in cakephp4, we are going to make use of the available FrozenTime class.
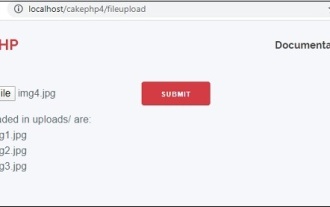 CakePHP File upload
Sep 10, 2024 pm 05:27 PM
CakePHP File upload
Sep 10, 2024 pm 05:27 PM
To work on file upload we are going to use the form helper. Here, is an example for file upload.
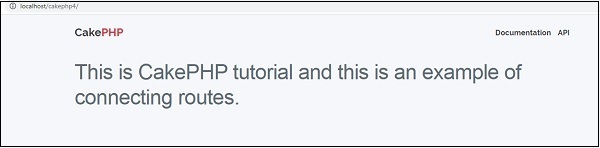 CakePHP Routing
Sep 10, 2024 pm 05:25 PM
CakePHP Routing
Sep 10, 2024 pm 05:25 PM
In this chapter, we are going to learn the following topics related to routing ?
 Discuss CakePHP
Sep 10, 2024 pm 05:28 PM
Discuss CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP is an open-source framework for PHP. It is intended to make developing, deploying and maintaining applications much easier. CakePHP is based on a MVC-like architecture that is both powerful and easy to grasp. Models, Views, and Controllers gu
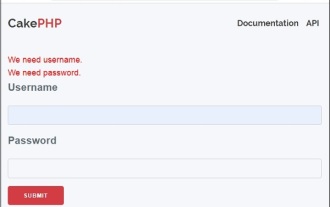 CakePHP Creating Validators
Sep 10, 2024 pm 05:26 PM
CakePHP Creating Validators
Sep 10, 2024 pm 05:26 PM
Validator can be created by adding the following two lines in the controller.
 How To Set Up Visual Studio Code (VS Code) for PHP Development
Dec 20, 2024 am 11:31 AM
How To Set Up Visual Studio Code (VS Code) for PHP Development
Dec 20, 2024 am 11:31 AM
Visual Studio Code, also known as VS Code, is a free source code editor — or integrated development environment (IDE) — available for all major operating systems. With a large collection of extensions for many programming languages, VS Code can be c





