How to use Kruskal's algorithm in C++

How to use the Kruskal algorithm in C
The Kruskal algorithm is a commonly used greedy algorithm to solve the minimum spanning tree problem. In programming using C, we can understand and use Kruskal's algorithm through simple code examples.
The basic idea of Kruskal's algorithm is to continuously select edges with the smallest edge weights that do not form a loop until all vertices are included in the spanning tree. Below we will introduce step by step how to implement Kruskal's algorithm using C.
Step One: Data Preparation
First, we need to prepare a graph data structure to represent the problem. In C, graphs can be represented using adjacency matrices or adjacency lists. Here we choose to use adjacency lists to represent undirected graphs.
Adjacency lists can be implemented using a combination of vectors and linked lists. We define two structures to represent the vertices and edges of the graph.
// 图的顶点结构体
struct Vertex {
int id; // 顶点的唯一标识符
// ...
};
// 图的边结构体
struct Edge {
int start; // 边的起始顶点
int end; // 边的结束顶点
int weight; // 边的权重
// ...
};
// 定义一个无向图的类
class Graph {
public:
// 添加顶点和边的函数
void addVertex(Vertex v);
void addEdge(Edge e);
// ...
private:
// 保存顶点和边的数据结构
vector<Vertex> vertices;
list<Edge> edges;
// ...
};Step 2: Implement the Kruskal algorithm
After preparing the data structure of the graph, we can start to implement the Kruskal algorithm. First, we need to sort the edges of the graph from small to large in weight. Then, we use Union-Find to determine whether the selected edges will form a cycle. Finally, we add the selected edges to the minimum spanning tree.
The following is the specific implementation code of Kruskal algorithm:
// 定义并查集结构体
struct UnionFind {
vector<int> parent;
// ...
};
// 初始化并查集
void initUnionFind(UnionFind& uf, int n) {
uf.parent.resize(n);
// ...
}
// 查找根节点
int findRoot(UnionFind& uf, int x) {
if (uf.parent[x] != x) {
uf.parent[x] = findRoot(uf, uf.parent[x]);
}
return uf.parent[x];
}
// 合并两个集合
void mergeSets(UnionFind& uf, int x, int y) {
int rootX = findRoot(uf, x);
int rootY = findRoot(uf, y);
if (rootX != rootY) {
uf.parent[rootX] = rootY;
}
}
// Kruskal算法主函数
list<Edge> kruskal(Graph& graph) {
list<Edge> minSpanningTree;
// 将图的边按照权重从小到大排序
graph.edges.sort([](const Edge& e1, const Edge& e2) {
return e1.weight < e2.weight;
});
int numVertices = graph.vertices.size();
UnionFind uf;
initUnionFind(uf, numVertices);
for (const Edge& edge : graph.edges) {
int startRoot = findRoot(uf, edge.start);
int endRoot = findRoot(uf, edge.end);
// 如果两个顶点不在同一个集合中,则添加该边到最小生成树中
if (startRoot != endRoot) {
minSpanningTree.push_back(edge);
mergeSets(uf, startRoot, endRoot);
}
}
return minSpanningTree;
}Step 3: Test code
Write a test function, create a graph and call Kruskal algorithm to output the minimum spanning tree:
void testKruskal() {
Graph graph;
// 添加顶点和边
// ...
list<Edge> minSpanningTree = kruskal(graph);
// 输出最小生成树
for (const Edge& edge : minSpanningTree) {
cout << edge.start << " -> " << edge.end << ", weight: " << edge.weight << endl;
}
}
int main() {
testKruskal();
return 0;
}The above is a simple example of using C to implement Kruskal's algorithm. Through this example, you can better understand and use Kruskal's algorithm to solve the minimum spanning tree problem.
The above is the detailed content of How to use Kruskal's algorithm in C++. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 How to use C++ to implement the scheduled task function of embedded systems
Aug 27, 2023 pm 12:05 PM
How to use C++ to implement the scheduled task function of embedded systems
Aug 27, 2023 pm 12:05 PM
How to use C++ to implement the scheduled task function of embedded systems. Embedded systems often need to implement the scheduled task function, that is, to execute some tasks within a specific time interval. As a powerful programming language, C++ provides us with many tools and libraries to achieve such functions. This article will introduce how to use the C++ programming language to implement scheduled task functions in embedded systems and provide some code examples. Using timer interrupts In embedded systems, we can use timer interrupts to implement scheduled task functions. By setting the timer
 How to use Kruskal's algorithm in C++
Sep 19, 2023 pm 04:10 PM
How to use Kruskal's algorithm in C++
Sep 19, 2023 pm 04:10 PM
How to use Kruskal's algorithm in C++ Kruskal's algorithm is a commonly used greedy algorithm to solve the minimum spanning tree problem. In programming in C++, we can understand and use Kruskal's algorithm through simple code examples. The basic idea of Kruskal's algorithm is to continuously select the edge with the smallest edge weight and which does not form a loop until all the vertices are included in the spanning tree. Below we will step by step introduce how to use C++ to implement Kruskal's algorithm. Step One: Data Preparation First, I
 Why does Prim and Kruskal's minimum spanning tree algorithm fail in directed graphs?
Sep 02, 2023 pm 05:29 PM
Why does Prim and Kruskal's minimum spanning tree algorithm fail in directed graphs?
Sep 02, 2023 pm 05:29 PM
Prim's method and Kruskal's algorithm are two common methods for locating MST (minimum spanning tree) in undirected graphs. However, these techniques cannot generate correct MST for directed graphs. This is because directed graphs do not fit the basic assumptions and methods used by Prim and Kruskal's algorithms. Prim's Algorithm First, there is Prim's algorithm, which involves adding edges to an expanding minimum spanning tree in a greedy manner until all vertices are covered. Vertices inside the MST are connected to vertices outside the MST through the edge with the lowest weight. Since all edges in an undirected graph can move in any direction, the shortest path from the MST to external vertices is easy to find. However, in a directed graph, the edges always point in one direction and there may not be a straight line
 High-speed retrieval algorithm and its application in PHP
Jun 22, 2023 pm 05:31 PM
High-speed retrieval algorithm and its application in PHP
Jun 22, 2023 pm 05:31 PM
As a popular server-side programming language, PHP plays an indispensable role in web application development. In actual development, we often need to perform operations such as retrieval and search on large amounts of data. At this time, high-speed retrieval algorithms have become a very important direction. This article will introduce high-speed retrieval algorithms commonly used in PHP and their applications. 1. Overview In the data structure, retrieval refers to finding data records with specified conditions in the data collection. Common retrieval methods include linear search, binary search, hash search, etc. linear search
 How to implement autonomous driving and intelligent transportation systems in C++?
Aug 26, 2023 am 08:58 AM
How to implement autonomous driving and intelligent transportation systems in C++?
Aug 26, 2023 am 08:58 AM
How to implement autonomous driving and intelligent transportation systems in C++? Autonomous driving and intelligent transportation systems are currently hot topics in the field of artificial intelligence, and their application areas involve many aspects such as transportation, safety protection, and urban planning. This article will explore how to use the C++ programming language to implement autonomous driving and intelligent transportation systems, and provide relevant code examples. Understand the basic principles of autonomous driving and intelligent transportation systems. Autonomous driving systems refer to technology that uses computers, sensors and other equipment to navigate and drive vehicles autonomously. it needs to be perceived in real time
 How to use C++ to implement an embedded system with real-time capabilities
Aug 25, 2023 pm 03:18 PM
How to use C++ to implement an embedded system with real-time capabilities
Aug 25, 2023 pm 03:18 PM
How to use C++ to implement an embedded system with real-time functions Introduction: With the continuous development of technology, embedded systems have been widely used in various fields. Real-time functionality is a crucial feature in embedded systems, especially in scenarios that require immediate response to external events. This article will introduce how to use C++ language to implement an embedded system with real-time functions and give code examples. Real-Time Operating System (RTOS) Real-time operating system (RTOS) is the key to achieving real-time functionality. RTOS has task scheduling,
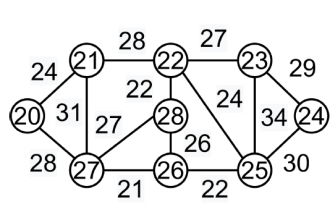 Kruskal's Minimum Spanning Tree Algorithm - Greedy Algorithm in C++
Aug 28, 2023 pm 03:05 PM
Kruskal's Minimum Spanning Tree Algorithm - Greedy Algorithm in C++
Aug 28, 2023 pm 03:05 PM
A spanning tree is a subgraph of a directed undirected graph that connects all vertices. There can be many spanning trees in a graph. The minimum spanning tree (MST) on each graph has the same or smaller weight than all other spanning trees. Weights are assigned to the edges of the spanning tree, and the sum is the weight assigned to each edge. Since V is the number of vertices in the graph, the number of edges of the minimum spanning tree is (V-1), where V is the number of edges. Use Kruskal's algorithm to find the minimum spanning tree. All edges should be arranged in non-descending order by weight. Choose the smallest side. If no loop is formed, the edge is included. Step 2 should be performed until the spanning tree has (V-1) edges. In this case, we are told to use the greedy approach. The greedy option is to choose the edge with the smallest weight. For example: the minimum spanning tree of this graph is (9-1)=8
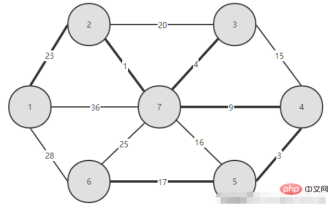 How to implement Kruskal algorithm in Java
May 11, 2023 pm 10:19 PM
How to implement Kruskal algorithm in Java
May 11, 2023 pm 10:19 PM
Introducing another algorithm for constructing a minimum spanning tree, namely the Kruskal algorithm: Let the graph G = (V, E) be an undirected connected weighted graph, V = {1, 2,...n}; let the minimum spanning tree T = (V, TE), the initial state of the tree is a non-connected graph with only n nodes and no edges T = (V, {}). Kruskal's algorithm treats these n nodes as n isolated connected branches. It first sorts all the edges according to their weights from small to large, and then if the number of edges to be selected in T is less than n-1, it makes a greedy selection like this: select the edge (i, j) with the smallest weight in the edge set E ), if adding edge (i, j) to the set TE does not produce a cycle, then add edge (i, j) to the edge set TE, that is, use edge (i, j) to merge the two branches into one




