How to implement Dijkstra's algorithm using Python?
Sep 21, 2023 pm 12:58 PM
How to implement Dijkstra's algorithm using Python?
Introduction:
Dijkstra's algorithm is a commonly used single-source shortest path algorithm that can be used to solve the shortest path problem between two vertices in a weighted graph. This article will introduce in detail how to use Python to implement Dijkstra's algorithm, including algorithm principles and specific code examples.
- Algorithm Principle
The core idea of Dijkstra's algorithm is to gradually determine the shortest path from the source point to other vertices by continuously selecting the vertex closest to the source point. The algorithm is mainly divided into the following steps:
(1) Initialization: Set the distance from the source point to other vertices to infinity, and the distance from the source point to itself to 0. At the same time, create a dictionary that records the shortest path and a collection that records the vertices that have been visited.
(2) Select the unvisited vertex currently closest to the source point, mark it as visited, and update the distance from the source point to its adjacent vertices.
(3) Repeat the above steps until all vertices have been visited or there are currently no selectable vertices. - Code implementation
The following is a code example using Python to implement Dijkstra's algorithm:
import sys
def dijkstra(graph, start):
# 初始化
distances = {vertex: sys.maxsize for vertex in graph} # 记录源点到各顶点的距离
distances[start] = 0
visited = set()
previous_vertices = {vertex: None for vertex in graph} # 记录最短路径的前驱结点
while graph:
# 选择当前距离源点最近的未访问顶点
current_vertex = min(
{vertex: distances[vertex] for vertex in graph if vertex not in visited},
key=distances.get
)
# 标记为已访问
visited.add(current_vertex)
# 更新当前顶点的相邻顶点的距离
for neighbor in graph[current_vertex]:
distance = distances[current_vertex] + graph[current_vertex][neighbor]
if distance < distances[neighbor]:
distances[neighbor] = distance
previous_vertices[neighbor] = current_vertex
# 当前顶点从图中移除
graph.pop(current_vertex)
return distances, previous_vertices
# 示例使用
if __name__ == '__main__':
# 定义图结构(字典表示)
graph = {
'A': {'B': 5, 'C': 1},
'B': {'A': 5, 'C': 2, 'D': 1},
'C': {'A': 1, 'B': 2, 'D': 4, 'E': 8},
'D': {'B': 1, 'C': 4, 'E': 3, 'F': 6},
'E': {'C': 8, 'D': 3},
'F': {'D': 6}
}
start_vertex = 'A'
distances, previous_vertices = dijkstra(graph, start_vertex)
# 打印结果
for vertex in distances:
path = []
current_vertex = vertex
while current_vertex is not None:
path.insert(0, current_vertex)
current_vertex = previous_vertices[current_vertex]
print(f'最短路径: {path}, 最短距离: {distances[vertex]}')The above code example shows how to use Dijkstra's algorithm to solve a given graph structure from the source point The shortest path and shortest distance to each vertex.
Conclusion:
This article introduces the principle of Dijkstra algorithm in detail and gives a code example of using Python to implement Dijkstra algorithm. Readers can modify and expand the sample code to apply to more complex scenarios. By mastering this algorithm, readers can better solve the problem of shortest paths in weighted graphs.
The above is the detailed content of How to implement Dijkstra's algorithm using Python?. For more information, please follow other related articles on the PHP Chinese website!

Hot Article

Hot tools Tags

Hot Article

Hot Article Tags

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 What are the advantages and disadvantages of templating?
May 08, 2024 pm 03:51 PM
What are the advantages and disadvantages of templating?
May 08, 2024 pm 03:51 PM
What are the advantages and disadvantages of templating?
 Google AI announces Gemini 1.5 Pro and Gemma 2 for developers
Jul 01, 2024 am 07:22 AM
Google AI announces Gemini 1.5 Pro and Gemma 2 for developers
Jul 01, 2024 am 07:22 AM
Google AI announces Gemini 1.5 Pro and Gemma 2 for developers
 For only $250, Hugging Face's technical director teaches you how to fine-tune Llama 3 step by step
May 06, 2024 pm 03:52 PM
For only $250, Hugging Face's technical director teaches you how to fine-tune Llama 3 step by step
May 06, 2024 pm 03:52 PM
For only $250, Hugging Face's technical director teaches you how to fine-tune Llama 3 step by step
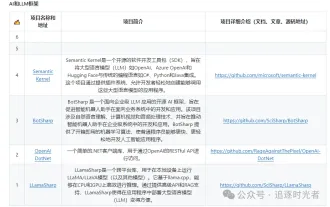 Share several .NET open source AI and LLM related project frameworks
May 06, 2024 pm 04:43 PM
Share several .NET open source AI and LLM related project frameworks
May 06, 2024 pm 04:43 PM
Share several .NET open source AI and LLM related project frameworks
 A complete guide to golang function debugging and analysis
May 06, 2024 pm 02:00 PM
A complete guide to golang function debugging and analysis
May 06, 2024 pm 02:00 PM
A complete guide to golang function debugging and analysis










