heptagon number
A heptagonal number is a number which can be represented as a heptagon. A heptagonal number can be represented as a combination of successive layers of heptagon( 7-sided polygon). be better explained with the below figures.

The first heptagon number is 1. Therefore, it can be represented by a small dot.
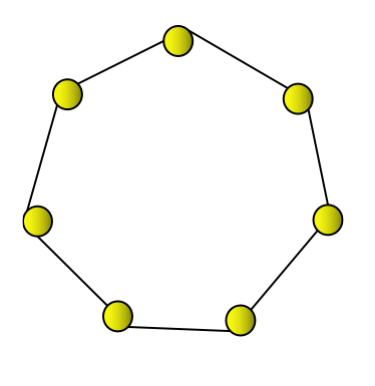
The second heptagonal number is 7, which can be represented by a heptagon.
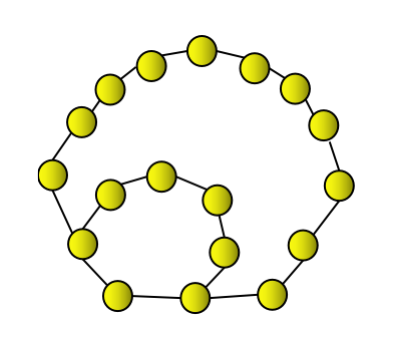
The third heptagon number is 18, which can be represented by a heptagon and combined with a continuous heptagon layer.
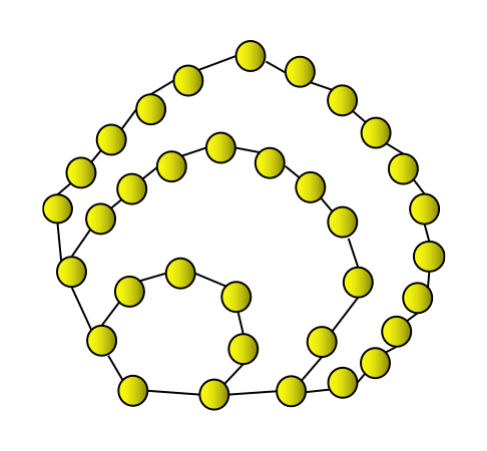
The fourth heptagonal number is 34. It can be represented in the way shown above as a heptagon plus two consecutive layers of heptagons, giving 34.
Similar concepts will be used for further heptagonal numbers. Following the same logic, the first few heptagonal numbers are 1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403……
In this problem, our task is to give any positive number N as input and print the Nth heptagon number as output.
For example,
INPUT : N=6
Output : 81
INPUT : N=9
Output: 189
Now let's look at the algorithm we will use to solve this problem.
algorithm
To solve this problem, we need to see the pattern followed by calculating the nth heptagonal number. The nth heptagonal number can be expressed as −
$$Heptagonal_{n}\:=\:\frac{n}{2}(5n\:-\:3)$$
If we look carefully at this expression, every heptagonal number has the following form
$\frac{n}{2}(5n\:-\:3)$, where n represents the number of heptagonal numbers.
Let us understand it better with examples.
For n=1, $\frac{1}{2}(5\:\times\:1\:-\:3)$= 1, which is the first heptagonal number.
For n=2, $\frac{2}{2}(5\:\times\:2\:-\:3)$= 7, which is the second heptagonal number.
When n=3, $\frac{3}{2}(5\:\times\:3\:-\:3)$= 18, which is the third heptagonal number.
Now, let us check the case of n=8. The result obtained by $\frac{8}{2}(5\:\times\:8\:-\:3)$ is 148, which is actually the eighth heptagonal number in the sequence of heptagonal numbers.
Since we can get any nth heptagonal number using the above expression, so in our method we will use this expression to calculate the nth heptagonal number, where n can be any positive number .
method
We will explain it in the following steps:
Take any positive number N as input and calculate the corresponding heptagon value N.
Initialize a function to calculate the Nth heptagon number.
Use the expression mentioned in the algorithm section, i.e. $\frac{N}{2}(5N\:-\:3)$, calculate the Nth heptagon number and store it in any in variables.
Returns the variable we stored, which will be the value of the Nth heptagonal number corresponding to any positive value N.
Note − We will use floating point data type instead of integer data type to avoid any errors due to decimal values when calculating the Nth heptagonal number using the above formula.
The Chinese translation ofExample
is:Example
Implement this method in C −
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
Output
1 2 |
|
Time complexity: O(1), Because it only takes constant time.
Space complexity: O(1), because no additional space is used.
in conclusion
We tried to learn the concept of heptagonal numbers and the formula for calculating the nth heptagonal number we used in the method.
I hope you found this article helpful in learning the concept of printing the nth heptagonal number entered by any user.
The above is the detailed content of heptagon number. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 37
37
 110
110
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
 Remove duplicate values from PHP array using regular expressions
Apr 26, 2024 pm 04:33 PM
Remove duplicate values from PHP array using regular expressions
Apr 26, 2024 pm 04:33 PM
How to remove duplicate values from PHP array using regular expressions: Use regular expression /(.*)(.+)/i to match and replace duplicates. Iterate through the array elements and check for matches using preg_match. If it matches, skip the value; otherwise, add it to a new array with no duplicate values.
 What is programming for and what is the use of learning it?
Apr 28, 2024 pm 01:34 PM
What is programming for and what is the use of learning it?
Apr 28, 2024 pm 01:34 PM
1. Programming can be used to develop various software and applications, including websites, mobile applications, games, and data analysis tools. Its application fields are very wide, covering almost all industries, including scientific research, health care, finance, education, entertainment, etc. 2. Learning programming can help us improve our problem-solving skills and logical thinking skills. During programming, we need to analyze and understand problems, find solutions, and translate them into code. This way of thinking can cultivate our analytical and abstract abilities and improve our ability to solve practical problems.
 MLP was killed overnight! MIT Caltech and other revolutionary KANs break records and discover mathematical theorems that crush DeepMind
May 06, 2024 pm 03:10 PM
MLP was killed overnight! MIT Caltech and other revolutionary KANs break records and discover mathematical theorems that crush DeepMind
May 06, 2024 pm 03:10 PM
Overnight, the machine learning paradigm is about to change! Today, the infrastructure that dominates the field of deep learning is the multilayer perceptron (MLP), which places activation functions on neurons. So, beyond that, are there any new routes we can take? Just today, teams from MIT, Caltech, Northeastern University and other institutions released a new neural network structure-Kolmogorov–Arnold Networks (KAN). The researchers made a simple change to the MLP by moving the learnable activation function from the nodes (neurons) to the edges (weights)! Paper address: https://arxiv.org/pdf/2404.19756 This change seems baseless at first glance
 Groundbreaking CVM algorithm solves more than 40 years of counting problems! Computer scientist flips coin to figure out unique word for 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Groundbreaking CVM algorithm solves more than 40 years of counting problems! Computer scientist flips coin to figure out unique word for 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Counting sounds simple, but in practice it is very difficult. Imagine you are transported to a pristine rainforest to conduct a wildlife census. Whenever you see an animal, take a photo. Digital cameras only record the total number of animals tracked, but you are interested in the number of unique animals, but there is no statistics. So what's the best way to access this unique animal population? At this point, you must be saying, start counting now and finally compare each new species from the photo to the list. However, this common counting method is sometimes not suitable for information amounts up to billions of entries. Computer scientists from the Indian Statistical Institute, UNL, and the National University of Singapore have proposed a new algorithm - CVM. It can approximate the calculation of different items in a long list.
 Problem-Solving with Python: Unlock Powerful Solutions as a Beginner Coder
Oct 11, 2024 pm 08:58 PM
Problem-Solving with Python: Unlock Powerful Solutions as a Beginner Coder
Oct 11, 2024 pm 08:58 PM
Pythonempowersbeginnersinproblem-solving.Itsuser-friendlysyntax,extensivelibrary,andfeaturessuchasvariables,conditionalstatements,andloopsenableefficientcodedevelopment.Frommanagingdatatocontrollingprogramflowandperformingrepetitivetasks,Pythonprovid
 Build browser-based applications with Golang
Apr 08, 2024 am 09:24 AM
Build browser-based applications with Golang
Apr 08, 2024 am 09:24 AM
Build browser-based applications with Golang Golang combines with JavaScript to build dynamic front-end experiences. Install Golang: Visit https://golang.org/doc/install. Set up a Golang project: Create a file called main.go. Using GorillaWebToolkit: Add GorillaWebToolkit code to handle HTTP requests. Create HTML template: Create index.html in the templates subdirectory, which is the main template.
 Collection of C++ programming puzzles: stimulate thinking and improve programming skills
Jun 01, 2024 pm 10:26 PM
Collection of C++ programming puzzles: stimulate thinking and improve programming skills
Jun 01, 2024 pm 10:26 PM
C++ programming puzzles cover algorithm and data structure concepts such as Fibonacci sequence, factorial, Hamming distance, maximum and minimum values of arrays, etc. By solving these puzzles, you can consolidate C++ knowledge and improve algorithm understanding and programming skills.




