How to calculate studentized residuals in Python?

Studentized residuals are often used in regression analysis to identify potential outliers in the data. Outliers are points that differ significantly from the overall trend of the data and can have a significant impact on the fitted model. By identifying and analyzing outliers, you can better understand underlying patterns in your data and improve the accuracy of your models. In this article, we will take a closer look at studentized residuals and how to implement it in python.

What is studentized residual?

The term "studentized residuals" refers to a specific class of residuals whose standard deviation is divided by the estimate. Regression analysis residuals describe the difference between the observed value of the response variable and its expected value generated by the model. To find outliers in the data that may significantly affect the fitted model, studentized residuals were used.

The following formula is usually used to calculate studentized residuals -

studentized residual = residual / (standard deviation of residuals * (1 - hii)^(1/2))

Where "residual" refers to the difference between the observed response value and the expected response value, "residual standard deviation" refers to the estimate of the residual standard deviation, and "hii" refers to the value of each data point Leverage factor.

Calculate studentized residuals using Python

statsmodels package can be used to calculate studentized residuals in Python. As an illustration, consider the following -

grammar

OLSResults.outlier_test()

Where OLSResults refers to the linear model fitted using the ols() method of statsmodels.

df = pd.DataFrame({'rating': [95, 82, 92, 90, 97, 85, 80, 70, 82, 83],
   'points': [22, 25, 17, 19, 26, 24, 9, 19, 11, 16]})

model = ols('rating ~ points', data=df).fit()
stud_res = model.outlier_test()

Where "rating" and "score" refer to simple linear regression.

algorithm

• Import numpy, pandas, Statsmodel api.

• Create a data set.

• Perform a simple linear regression model on the data set.

• Calculate studentized residuals.

• Print studentized residuals.

Example

Here is a demonstration of using the scikit-posthocs library to run Dunn's tests -

#import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols

#create dataset
df = pd.DataFrame({'rating': [95, 82, 92, 90, 97, 85, 80, 70, 82, 83], 'points': [22, 25, 17, 19, 26, 24, 9, 19, 11, 16]})

Next use the statsmodels OLS class to create a linear regression model -

#fit simple linear regression model
model = ols('rating ~ points', data=df).fit()

Using the outlier test() method, the studentized residuals of each observation in the data set can be generated in the DataFrame -

#calculate studentized residuals
stud_res = model.outlier_test()

#display studentized residuals
print(stud_res)

Output

  student_resid   unadj_p   bonf(p)
0       1.048218  0.329376  1.000000
1      -1.018535  0.342328  1.000000
2       0.994962  0.352896  1.000000
3       0.548454  0.600426  1.000000
4       1.125756  0.297380  1.000000
5      -0.465472  0.655728  1.000000
6      -0.029670  0.977158  1.000000
7      -2.940743  0.021690  0.216903
8       0.100759  0.922567  1.000000
9      -0.134123  0.897080  1.000000

We can also quickly plot predictor values ​​based on studentized residuals -

grammar

x = df['points']
y = stud_res['student_resid']

plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals')

Here we will use the matpotlib library to draw the chart with color = 'black' and lifestyle = '--'

algorithm

• Import matplotlib’s pyplot library

• Define predictor values

• Define studentized residual

• Create a scatterplot of predictors versus studentized residuals

Example

import matplotlib.pyplot as plt

#define predictor variable values and studentized residuals
x = df['points']
y = stud_res['student_resid']

#create scatterplot of predictor variable vs. studentized residuals
plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals')

Output

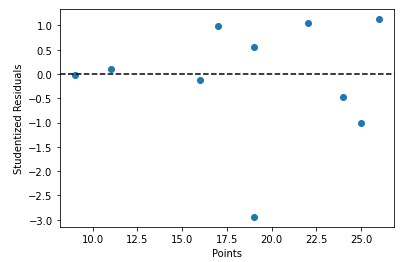
in conclusion

Identify and evaluate possible data outliers. Examining studentized residuals allows you to find points that deviate significantly from the overall trend of the data and explore why they affect the fitted model. Identifying significant observations Studentized residuals can be used to discover and evaluate influential data that have a significant impact on the fitted model. Look for high leverage spots. Studentized residuals can be used to identify high leverage points. Leverage is a measure of the influence of a certain point on the fitted model. Overall, using studentized residuals helps analyze and improve the performance of regression models.

The above is the detailed content of How to calculate studentized residuals in Python?. For more information, please follow other related articles on the PHP Chinese website!