 Technology peripherals
Technology peripherals
 AI
AI
 Revisit Turing's principle and feel the power of proof by contradiction
Revisit Turing's principle and feel the power of proof by contradiction
Revisit Turing's principle and feel the power of proof by contradiction
Algorithms have become ubiquitous, and it seems that for every problem that can be expressed in precise mathematical terms, there is a corresponding algorithm. However, this is not the case. In fact, some seemingly simple problems can never be solved by algorithms. Alan Turing, a pioneer among computer scientists, proved this in a paper nearly a century ago. Because of the existence of such "uncomputable" problems, he proposed the computational mathematical model that launched modern computer science.
Turing demonstrated this groundbreaking result using a counterintuitive strategy: He defined a problem that resisted all attempts to solve it. "For example, if I ask you what you are doing, no matter what your answer is, I will say, 'What I am going to do is different from what you said,'" said Rahul Ilango, a graduate student at MIT studying theoretical computer science. Rewritten content: Turing demonstrated this groundbreaking result with a counterintuitive strategy: he defined a problem that resisted all attempts to solve it. "For example, if I ask you what you are doing, no matter what your answer is, I will say, 'What I am going to do is different from what you said.'" said Rahul Ilango, a graduate student at MIT studying theoretical computer science
Turing's strategy is based on a long-standing mathematical method called the "diagonal proof." The following is a simplified explanation of the logic behind his proof
StringThe diagonal proof comes from a clever trick to solve a problem about strings. The value of each bit can be 0 or 1. The description of the problem is: Given a list of strings, all strings in the list are the same length, how can you generate a new string that is not in the list?
Rewritten content: One of the most straightforward strategies is to consider every possible string in order. Suppose there are five strings, each with five bits. First iterate over to check if 00000 exists in the list. If it doesn't exist, the problem is solved; if it exists, go to 00001 and repeat the process. This method is simple, but slow for long lists resulting from long strings
Diagonal turns out to be a viable alternative for incrementally building non-existent strings. Starting with the first bit of the first string in the list, reverse it and this will become the first bit of the new string. Then reverse the second bit of the second string and use it as the second bit of the new string, repeat this until you reach the end of the list. By reversing the bit operations, you ensure that the new string is different from every string in the original list by at least one position. (They also form a diagonal line in the list of strings, so it is called a diagonal proof.)
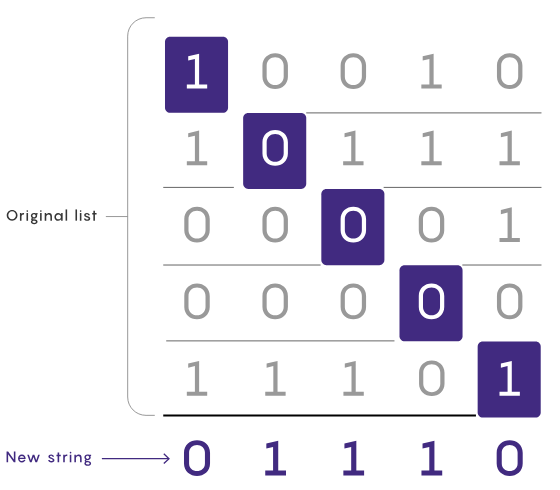 The diagonal proof simply requires checking each item in the list in turn. one bit in a string, so it's usually much faster than other methods, but its real power lies in how well it handles infinitely long string problems.
The diagonal proof simply requires checking each item in the list in turn. one bit in a string, so it's usually much faster than other methods, but its real power lies in how well it handles infinitely long string problems.
Ryan Williams, a theoretical computer scientist at MIT, said: "Although strings and lists can be infinite, the diagonalization method is still effective."
George Cantor Erl was the first to harness this power and was the founder of the mathematical field of set theory. In 1873, he used diagonals to show that some infinite values are larger than others. Sixty years later, Turing applied this version of the diagonal proof to the theory of computation
Restrictions of AlgorithmsIn order to prove that there is a class of mathematical problems that are impossible Solved by any algorithm, Turing proposed a theory. This type of problem has well-defined inputs and outputs, but no defined process to convert the inputs into outputs. Turing focused primarily on decision-making problems and sought to better concretize this nebulous task. In a decision problem, the input can be any string consisting of 0 and 1, and the output can be 0 or 1
Determining whether a number is prime (divisible only by 1 and itself) is a decision An example of the problem - given an input string representing a number, the correct output is 1 if the number is prime and 0 if it is not prime. Another example is checking computer programs for syntax errors. The input strings represent code for different programs - all programs can be represented this way because that's how they are stored and executed on the computer - the rule is that if the code contains a syntax error, output 1, if not, Then output 0.
Only if an algorithm produces the correct output for every possible input, it can be said to solve the problem - if it fails even once, it is not a general algorithm for solving the problem. Typically, one specifies a problem that one wants to solve and then tries to find an algorithm to solve it. Turing turned this logic on its head when looking for unsolvable problems - he imagined an infinite list of all possible algorithms and used diagonalization to construct a puzzle that was opposed to every algorithm on the list .
Please imagine a new question consisting of 20 questions. Instead of starting from a specific concept, the answerer comes up with an example of dissatisfaction for each question in turn. When the game is over, the answerer has described a proposition consisting entirely of opposites of the question
Turing's diagonal proof process is to perform each algorithm in an infinitely long list of algorithms. Thinking: "Can this algorithm solve the problem we want to prove to be uncomputable?", like a game competition. Williams said: "This method transforms the original problem into an 'infinite problem.'"
To win the game, Turing needs to design a question in which the answer given by each algorithm is no. of. This means finding the specific input that made the first algorithm output the wrong answer, another input that made the second algorithm fail, and so on. He found that these special inputs used a method similar to that used by Kurt Gödel not long ago when he showed that self-referential assertions like "This proposition is not provable" can cause trouble in the foundation of mathematics. skills.
The key here is that every algorithm (or program) can be represented as a string of 0s and 1s. This means that, just like in the error checker example, an algorithm can take as input the encoding of another algorithm. In principle, the algorithm could even take its own encoding as input.
In this way, we can define a non-computable problem, just like the problem mentioned in Turing's proof: "Given an input string representing the code of an algorithm, when the code of the algorithm itself As input, if the algorithm outputs 0, let it output 1, otherwise it outputs 0." Every algorithm that attempts to solve this problem will produce incorrect output on at least one input, namely the input that corresponds to its own code. This means that this anomalous problem cannot be solved by any algorithm
What cannot be proved is proof by contradiction
The use of diagonal proofs by computer scientists does not end here. Finish. In 1965, Juris Hartmanis and Richard Stearns adapted Turing's argument to show that not all computable problems are equal—some are inherently more difficult than others. This result launched the field of computational complexity theory, the study of the difficulty of computational problems.
The development of complexity theory reveals the limitations of Turing's diagonal proof. In 1975, Baker, Gill, and Solovy showed that many unsolved problems in complexity theory could not be solved by diagonalization alone. The most important of them is the famous P/NP problem, which is simply a question about whether the correctness of the solution can be verified in polynomial time and whether it can be solved in polynomial time
Diagonal proof The limitations of are a direct result of the high level of abstraction that makes it so powerful. Turing's proof did not address any of the non-computable problems that might arise in practice - instead, problems tend to be abstract. Other diagonals prove equally far removed from the real world, so they cannot solve real-world problems.
Williams said: "The diagonal proof does not directly touch the problem itself, just like doing an experiment with a glove box."
The declining trend of the diagonal proof shows that solving P The /NP problem is going to be a long journey. Despite its limitations, diagonal proofs remain one of the key tools in the complexity theorist's arsenal. In 2011, Williams combined it with a range of other techniques to demonstrate that a restricted computational model was incapable of solving some incredibly difficult problems—a result that solved a problem that had vexed researchers for 25 years. While this is far from solving the P/NP problem, it still represents significant progress.
If you want to prove something is impossible, don’t underestimate the power of denial
Original link:
Needs rewriting The content is: https://www.quantamagazine.org/alan-turing-and-the-power-of-negative-thinking-20230905/
The above is the detailed content of Revisit Turing's principle and feel the power of proof by contradiction. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 A Diffusion Model Tutorial Worth Your Time, from Purdue University
Apr 07, 2024 am 09:01 AM
A Diffusion Model Tutorial Worth Your Time, from Purdue University
Apr 07, 2024 am 09:01 AM
Diffusion can not only imitate better, but also "create". The diffusion model (DiffusionModel) is an image generation model. Compared with the well-known algorithms such as GAN and VAE in the field of AI, the diffusion model takes a different approach. Its main idea is a process of first adding noise to the image and then gradually denoising it. How to denoise and restore the original image is the core part of the algorithm. The final algorithm is able to generate an image from a random noisy image. In recent years, the phenomenal growth of generative AI has enabled many exciting applications in text-to-image generation, video generation, and more. The basic principle behind these generative tools is the concept of diffusion, a special sampling mechanism that overcomes the limitations of previous methods.
 Generate PPT with one click! Kimi: Let the 'PPT migrant workers' become popular first
Aug 01, 2024 pm 03:28 PM
Generate PPT with one click! Kimi: Let the 'PPT migrant workers' become popular first
Aug 01, 2024 pm 03:28 PM
Kimi: In just one sentence, in just ten seconds, a PPT will be ready. PPT is so annoying! To hold a meeting, you need to have a PPT; to write a weekly report, you need to have a PPT; to make an investment, you need to show a PPT; even when you accuse someone of cheating, you have to send a PPT. College is more like studying a PPT major. You watch PPT in class and do PPT after class. Perhaps, when Dennis Austin invented PPT 37 years ago, he did not expect that one day PPT would become so widespread. Talking about our hard experience of making PPT brings tears to our eyes. "It took three months to make a PPT of more than 20 pages, and I revised it dozens of times. I felt like vomiting when I saw the PPT." "At my peak, I did five PPTs a day, and even my breathing was PPT." If you have an impromptu meeting, you should do it
 All CVPR 2024 awards announced! Nearly 10,000 people attended the conference offline, and a Chinese researcher from Google won the best paper award
Jun 20, 2024 pm 05:43 PM
All CVPR 2024 awards announced! Nearly 10,000 people attended the conference offline, and a Chinese researcher from Google won the best paper award
Jun 20, 2024 pm 05:43 PM
In the early morning of June 20th, Beijing time, CVPR2024, the top international computer vision conference held in Seattle, officially announced the best paper and other awards. This year, a total of 10 papers won awards, including 2 best papers and 2 best student papers. In addition, there were 2 best paper nominations and 4 best student paper nominations. The top conference in the field of computer vision (CV) is CVPR, which attracts a large number of research institutions and universities every year. According to statistics, a total of 11,532 papers were submitted this year, and 2,719 were accepted, with an acceptance rate of 23.6%. According to Georgia Institute of Technology’s statistical analysis of CVPR2024 data, from the perspective of research topics, the largest number of papers is image and video synthesis and generation (Imageandvideosyn
 From bare metal to a large model with 70 billion parameters, here is a tutorial and ready-to-use scripts
Jul 24, 2024 pm 08:13 PM
From bare metal to a large model with 70 billion parameters, here is a tutorial and ready-to-use scripts
Jul 24, 2024 pm 08:13 PM
We know that LLM is trained on large-scale computer clusters using massive data. This site has introduced many methods and technologies used to assist and improve the LLM training process. Today, what we want to share is an article that goes deep into the underlying technology and introduces how to turn a bunch of "bare metals" without even an operating system into a computer cluster for training LLM. This article comes from Imbue, an AI startup that strives to achieve general intelligence by understanding how machines think. Of course, turning a bunch of "bare metal" without an operating system into a computer cluster for training LLM is not an easy process, full of exploration and trial and error, but Imbue finally successfully trained an LLM with 70 billion parameters. and in the process accumulate
 PyCharm Community Edition Installation Guide: Quickly master all the steps
Jan 27, 2024 am 09:10 AM
PyCharm Community Edition Installation Guide: Quickly master all the steps
Jan 27, 2024 am 09:10 AM
Quick Start with PyCharm Community Edition: Detailed Installation Tutorial Full Analysis Introduction: PyCharm is a powerful Python integrated development environment (IDE) that provides a comprehensive set of tools to help developers write Python code more efficiently. This article will introduce in detail how to install PyCharm Community Edition and provide specific code examples to help beginners get started quickly. Step 1: Download and install PyCharm Community Edition To use PyCharm, you first need to download it from its official website
 Five programming software for getting started with learning C language
Feb 19, 2024 pm 04:51 PM
Five programming software for getting started with learning C language
Feb 19, 2024 pm 04:51 PM
As a widely used programming language, C language is one of the basic languages that must be learned for those who want to engage in computer programming. However, for beginners, learning a new programming language can be difficult, especially due to the lack of relevant learning tools and teaching materials. In this article, I will introduce five programming software to help beginners get started with C language and help you get started quickly. The first programming software was Code::Blocks. Code::Blocks is a free, open source integrated development environment (IDE) for
 AI in use | AI created a life vlog of a girl living alone, which received tens of thousands of likes in 3 days
Aug 07, 2024 pm 10:53 PM
AI in use | AI created a life vlog of a girl living alone, which received tens of thousands of likes in 3 days
Aug 07, 2024 pm 10:53 PM
Editor of the Machine Power Report: Yang Wen The wave of artificial intelligence represented by large models and AIGC has been quietly changing the way we live and work, but most people still don’t know how to use it. Therefore, we have launched the "AI in Use" column to introduce in detail how to use AI through intuitive, interesting and concise artificial intelligence use cases and stimulate everyone's thinking. We also welcome readers to submit innovative, hands-on use cases. Video link: https://mp.weixin.qq.com/s/2hX_i7li3RqdE4u016yGhQ Recently, the life vlog of a girl living alone became popular on Xiaohongshu. An illustration-style animation, coupled with a few healing words, can be easily picked up in just a few days.
 A must-read for technical beginners: Analysis of the difficulty levels of C language and Python
Mar 22, 2024 am 10:21 AM
A must-read for technical beginners: Analysis of the difficulty levels of C language and Python
Mar 22, 2024 am 10:21 AM
Title: A must-read for technical beginners: Difficulty analysis of C language and Python, requiring specific code examples In today's digital age, programming technology has become an increasingly important ability. Whether you want to work in fields such as software development, data analysis, artificial intelligence, or just learn programming out of interest, choosing a suitable programming language is the first step. Among many programming languages, C language and Python are two widely used programming languages, each with its own characteristics. This article will analyze the difficulty levels of C language and Python



