
Use the Gaussian mixture model to split the one-dimensional multimodal distribution into multiple distributions
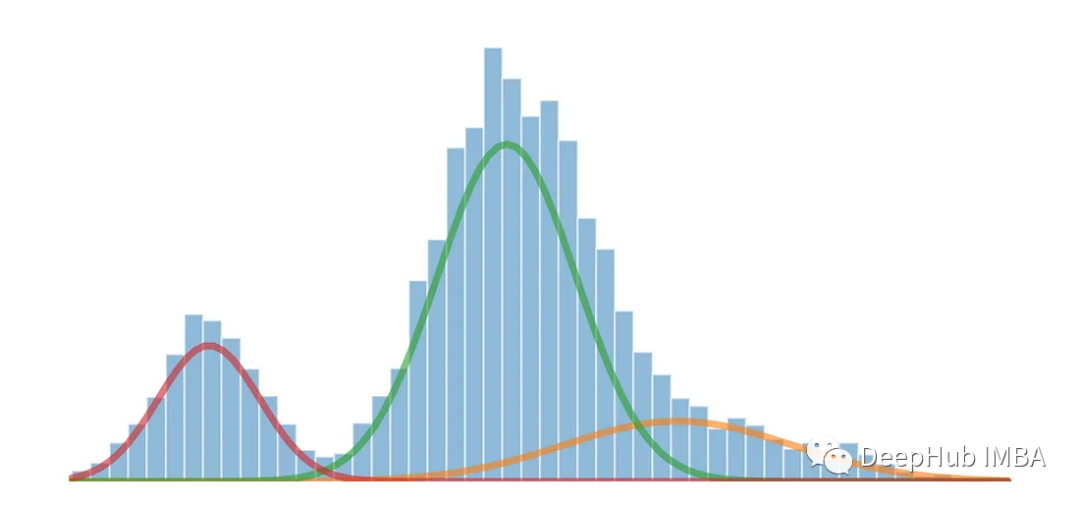
Gaussian mixture model (Gaussian Mixture Models (GMM for short) is a probabilistic model commonly used in the fields of statistics and machine learning for modeling and analyzing complex data distributions. GMM is a generative model that assumes that the observed data is composed of multiple Gaussian distributions, each Gaussian distribution is called a component, and these components control their contribution in the data through weights.
When a data set shows multiple different peaks or modes, it usually means There are multiple prominent clusters or concentrations of data points in the data set. Each mode represents a prominent cluster or concentration of data points in the distribution and can be thought of as a high-density region where data values are more likely to occur
We will use the one-dimensional numpy-generated array.
import numpy as np dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500) multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)
Let us visualize the one-dimensional data distribution.
import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid') plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()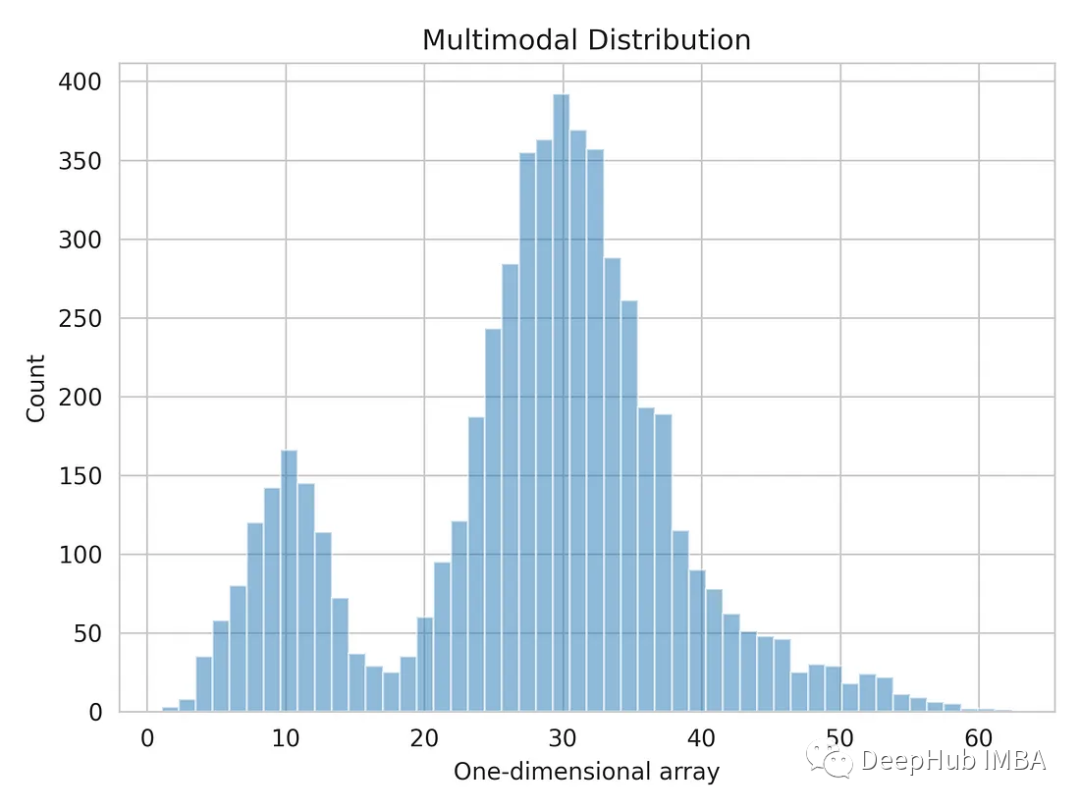
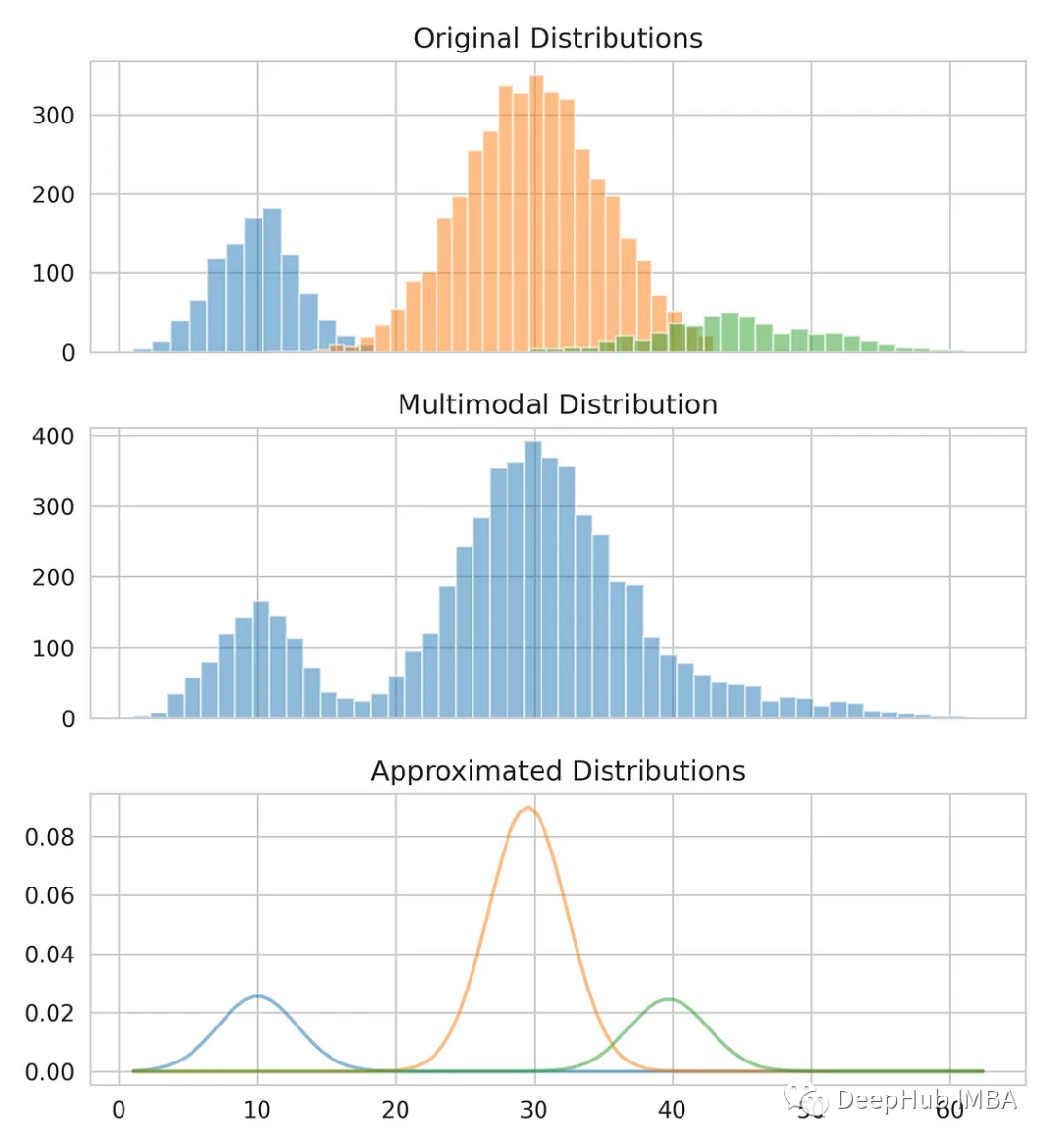
We will use Gaussian mixture model to calculate the mean and standard deviation of each distribution, separating the multimodal distribution into three original distributions. The Gaussian mixture model is an unsupervised probabilistic model that can be used for data clustering. It uses the expectation maximization algorithm to estimate the density region
from sklearn.mixture import GaussianMixture gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1)) means = gmm.means_ # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5 # Useful when plotting the distributions later weights = gmm.weights_ print(f"Means: {means}, Standard Deviations: {standard_deviations}") #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]We already have the mean and standard deviation and can model the original distribution. You can see that while the mean and standard deviation may not be exactly correct, they provide a close estimate.
Compare our estimates with the original data.
from scipy.stats import norm fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7)) for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):axes[0].hist(dist, bins=bins, alpha=0.5) axes[1].hist(multimodal_dist, bins=50, alpha=0.5) x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100) for mean, covariance, weight in zip(means, standard_deviations, weights):pdf = weight*norm.pdf(x, mean, std)plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5) plt.show()
Gaussian mixture model is a powerful tool that can be used to analyze complex It is used to model and analyze data distribution and is also one of the foundations of many machine learning algorithms. It has a wide range of applications and can solve a variety of data modeling and analysis problems
This method can be used as a feature engineering technique to estimate the confidence interval of a subdistribution within an input variable
The above is the detailed content of Decomposing multimodal distributions using Gaussian mixture models. For more information, please follow other related articles on the PHP Chinese website!




