 Technology peripherals
Technology peripherals
 AI
AI
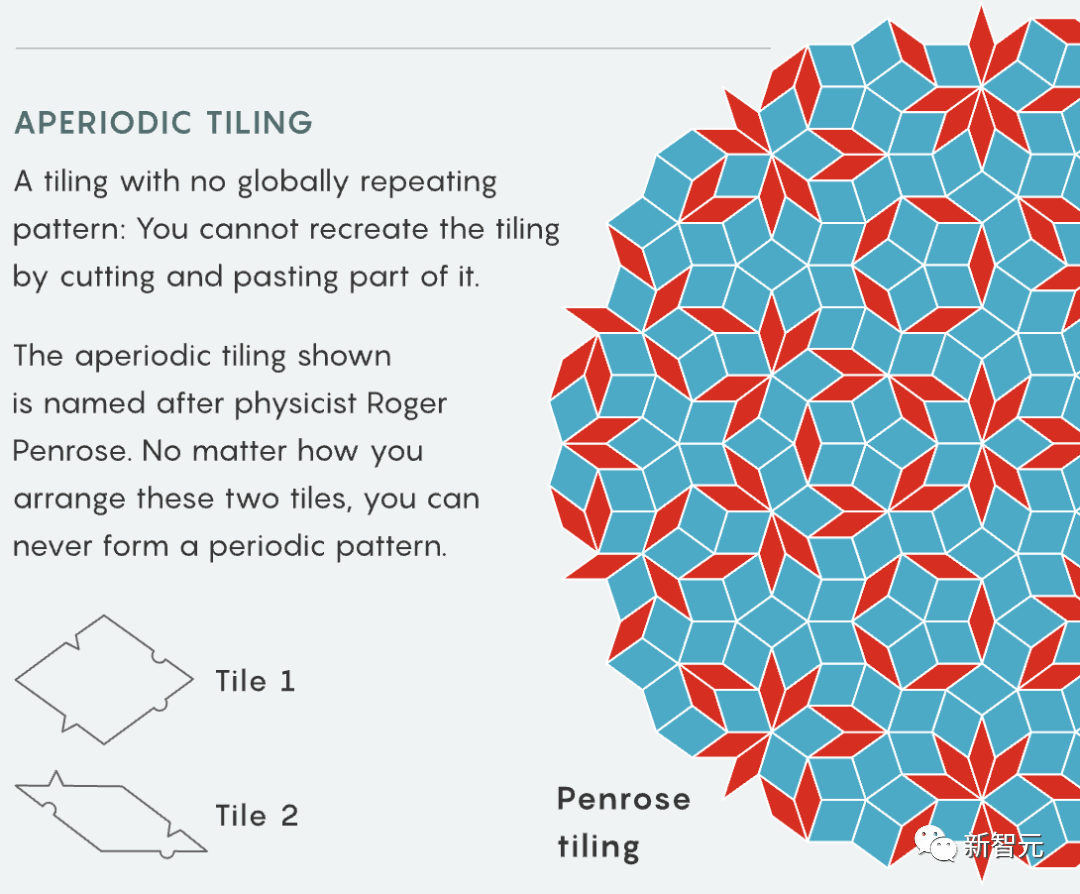
 Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving
Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving
Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving
Tao Zhexuan made a new breakthrough in studying the periodic dense paving problem
On September 18, Tao Zhexuan and Rachel Greenfeld published the preprinted paper "Translational Single Mingling Pavement" "Undecidability of translational monotilings" was uploaded to arXiv.

Paper address: https://arxiv.org/abs/2309.09504
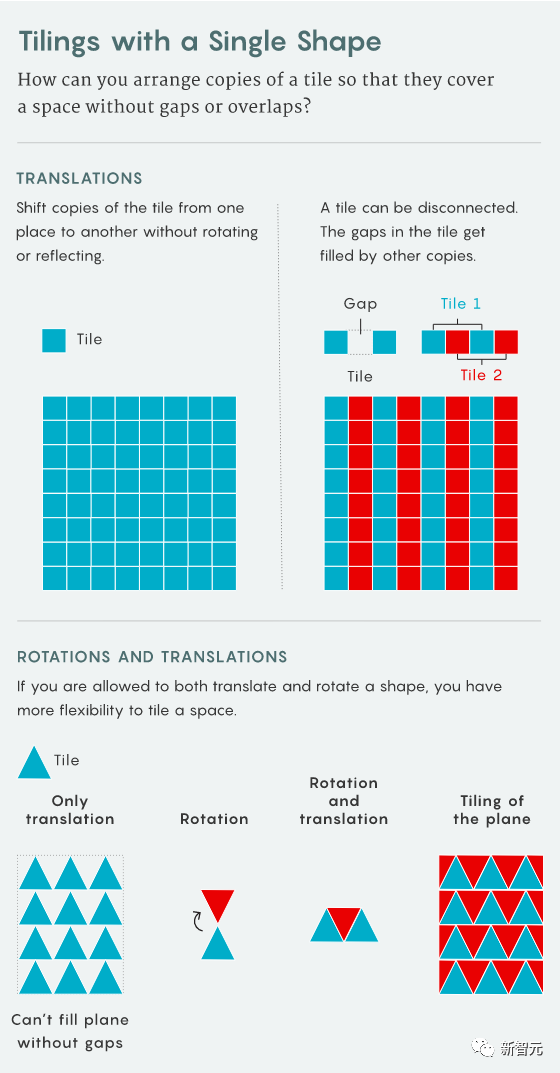
This paper The main conclusion is that if the dimensions of the grid are unbounded, then the problem of determining whether a finite subset of the grid can tile a periodic subset of the grid is undecidable
Be aware that this problem is decidable in dimension 1 and dimension 2.
Tao Zhexuan said that it is a bit strange that most of the components demonstrated in the article are similar to popular games——
There are dense analogues of dominoes, Sudoku, the computer game "Tetris", and even the children's game "Fizz buzz"
Why study one Why do math problems involve so many games? Terence Tao also cannot explain

The undecidability of translational single dense tiling
This paper, It is a sequel to the two's previous paper. Link Periodic Tiles Problem
In the last paper, they constructed a high-dimensional grid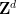 The translation of the single dense pavement
The translation of the single dense pavement 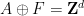
(therefore the single dense pavement 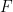 is a finite set), which is non-periodic (There is no way to "fix" this tile into a periodic tile
is a finite set), which is non-periodic (There is no way to "fix" this tile into a periodic tile  , where
, where 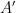 is now relative to the finite index subgroup
is now relative to the finite index subgroup  is periodic).
is periodic).

This fact negates the hypothesis of Stein, Grunbaum-Shephard and Lagarias-Wang about the non-existence of aperiodic closely packed monomers
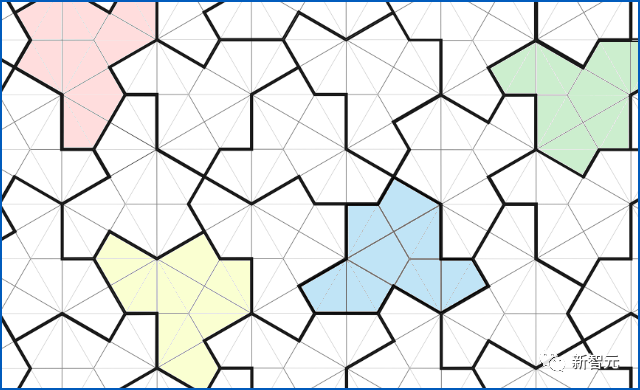
("Hat single dense paving" is a recently discovered non-periodic equidistant single dense paving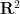 . In this kind of single dense paving, it is allowed to use Rotation, reflection and translation, or the newer "ghost monolith". These monoliths are similar to hat monoliths, except no reflection is required).
. In this kind of single dense paving, it is allowed to use Rotation, reflection and translation, or the newer "ghost monolith". These monoliths are similar to hat monoliths, except no reflection is required).
One of the reasons why Terence Tao and Rachel Greenfeld inspired this conjecture is the observation of mathematician Hao Wang

He found that if the periodic tessellation conjecture is true, then the translational tessellation problem is algorithmically decidable——
There is a Turing machine, for  , when given a dimension
, when given a dimension 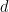 and a finite subset
and a finite subset 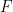 At this time, you can determine within a limited time whether
At this time, you can determine within a limited time whether 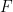 can be densely paved
can be densely paved 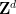 .
.
This is because if there is a periodic tiling, it can be found through a computer search
If there is no tiling at all, Then it can be known from the compactness theorem that there are some limited  subsets that cannot be covered by
subsets that cannot be covered by 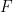 disjoint translations. This can also be done by computer Search to discover.
disjoint translations. This can also be done by computer Search to discover.
The periodic tessellation conjecture asserts that these are the only two possible situations, thus giving decidability.

On the other hand, Wang’s point of view is immutable: the failure of the periodic tessellation conjecture does not automatically mean that the translational tessellation conjecture The undecidability of the problem, since it does not rule out the existence of other algorithms to determine the tiling that do not depend on the existence of periodic tiling
(e.g. even if With the newly discovered hat and ghost tiling, it is still an open question whether the isometric single tiling problem of polygons with rational coefficients in 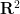 is decidable, whether or not it has reflections.
is decidable, whether or not it has reflections.
The main results of this article address this issue (with a caveat):

What needs to be rewritten is: Theorem 1
does not exist any algorithm, for 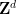 , given a dimension
, given a dimension  , a periodic subset
, a periodic subset 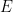 , and a finite subset
, and a finite subset 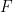 , which can determine whether there is a translational tiling in a limited time
, which can determine whether there is a translational tiling in a limited time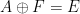 .
.
It should be noted that the periodic subset 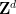 of
of  must be used instead of all
must be used instead of all  ; This is largely due to technical limitations of this approach and is likely to be eliminated with additional effort and creativity.
; This is largely due to technical limitations of this approach and is likely to be eliminated with additional effort and creativity.
In addition, Terence Tao and Rachel Greenfeld also noticed that when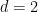 , the periodic pavement conjecture was established by Bhattacharya, so in
, the periodic pavement conjecture was established by Bhattacharya, so in In this case, the problem can be determined.
In this case, the problem can be determined.
For any fixed value of 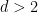 , it is still open whether the tiling problem is decidable (note that in the above results, the dimension
, it is still open whether the tiling problem is decidable (note that in the above results, the dimension 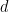 is not fixed, but part of the input).
is not fixed, but part of the input).
This theorem also implies that due to the well-known connection between algorithmic undecidability and logical undecidability (also known as logical independence) It turns out that there exists a (in principle unambiguously describable) periodic subset of the dimensions  ,
, 
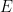 ,# The finite subset
,# The finite subset 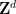 of
of  ##, so that
##, so that 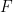 can be passed through translational tiling
can be passed through translational tiling 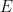 cannot be used in ZFC set theory Confirm or falsify (assuming of course that the theory is consistent).
cannot be used in ZFC set theory Confirm or falsify (assuming of course that the theory is consistent).
As a result of this approach, we can also use the "almost two-dimensional" group  instead of ## here #, where
instead of ## here #, where 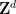 is a finite abelian group (now part of the input, instead of dimension
is a finite abelian group (now part of the input, instead of dimension 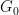 ).
). 
A common way to prove that a problem is undecidable is to "encode" other problems that are known to be undecidable into the original problem, so that any algorithm that determines the original problem can also determine it. Embedded Question
Therefore, we encode Wang’s dense paving problem as a single dense paving problem The second question is about the Wang’s secret shop problem Given a limited Wang’s secret shop set Berger once famously concluded that this question cannot be determined The content that needs to be rewritten is: Berger, Robert, Converting this problem into a high-dimensional translational single dense tiling problem requires solving some intermediate problems First, we can easily embed the Wang's secret shop problem into a similar problem, which we call the domino problem: Rewritten as follows: Domino problem is problem 3 Given a level (or vertical) finite set of dominoes In fact, we only need to insert each Wang's tile as a separate "point" and define the domino set In the next steps we will combine the domino problem with the Sudoku problem: Question 4 (Sudoku problem) Given column width Embedding the Sudoku problem into the single dense pavement problem is based on the modification method proposed in previous papers These papers also proposed Different versions of Sudoku problems, and created a method called "Tab Language" that can transform various problems (including Sudoku problems) into a single Tile Problem To encode a domino problem as a Sudoku problem, we need to get a domino function (which obeys the same rules as certain domino sets This approach is not immediately obvious, but Tao and Rachel Greenfeld adapted some of Aanderaa and Lewis's ideas with the help of Emmanuel Jeandel, and certain hierarchies were used to encode one question into another. Here we explain the hierarchical structure Then, use the formula is two different large prime numbers (for example, you can take ,and , the first component of (1) looks like this: looks like this:  :
: 
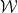 (unit (square, each edge assigned a certain color from a limited palette), is it possible to tessellate a plane using a standard grid
(unit (square, each edge assigned a certain color from a limited palette), is it possible to tessellate a plane using a standard grid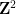 by translation so that adjacent tiles are in common Have the same color on the edges?
by translation so that adjacent tiles are in common Have the same color on the edges? 


 or
or  , which are a pair of adjacent unit squares, each unit square is represented by a finite set ## To decorate it with an element point in
, which are a pair of adjacent unit squares, each unit square is represented by a finite set ## To decorate it with an element point in 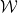 #, is it possible to assign a point to each unit square in the standard lattice tiling
#, is it possible to assign a point to each unit square in the standard lattice tiling 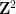 , so that each pair in this tiling Can horizontal (or vertical) squares use dominoes from
, so that each pair in this tiling Can horizontal (or vertical) squares use dominoes from 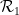 or
or 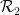 ?
? 
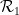 ,
,  are pairs of Wang's dense tiles that are adjacent horizontally or vertically and have the same edge color.
are pairs of Wang's dense tiles that are adjacent horizontally or vertically and have the same edge color. 
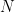 , set of numbers
, set of numbers 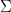 , set of functions
, set of functions 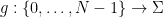
 , and "initial conditions"
, and "initial conditions" 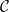 (I won’t go into details here), is it possible to assign a number to each cell
(I won’t go into details here), is it possible to assign a number to each cell 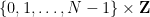 in the "Sudoku board"
in the "Sudoku board"  ## so that for any slope
## so that for any slope 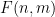 and intercept
and intercept 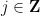 , the number
, the number 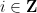 # along the
# along the 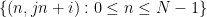 line ## is located in
line ## is located in 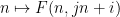 (and
(and 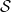 is subject to the initial condition
is subject to the initial condition 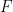 )?
)? 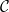
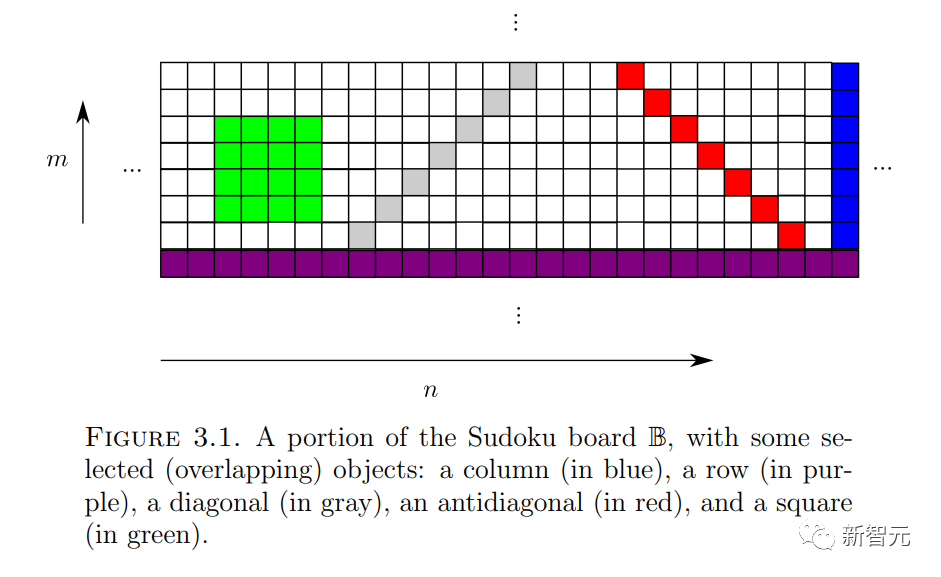 The most novel part of this paper is to prove that the domino problem can indeed be embedded in a Sudoku problem.
The most novel part of this paper is to prove that the domino problem can indeed be embedded in a Sudoku problem. 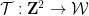 associated domino constraints) and use it to construct the Sudoku function
associated domino constraints) and use it to construct the Sudoku function 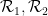 (which obeys some Sudoku constraints associated with the domino set); conversely, each obeys the Sudoku puzzle rules Sudoku functions must be generated from domino functions in some way.
(which obeys some Sudoku constraints associated with the domino set); conversely, each obeys the Sudoku puzzle rules Sudoku functions must be generated from domino functions in some way. 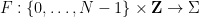

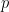 (due to the two-dimensional nature of the domino problem, two different primes need to be used).
(due to the two-dimensional nature of the domino problem, two different primes need to be used). 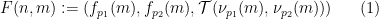 to construct the Sudoku function
to construct the Sudoku function 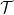 , which There will be some kind of embedding.
, which There will be some kind of embedding. 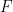 where
where 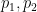 ,
, 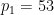 ),
), 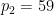 represents the number of times
represents the number of times 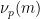 is divided by
is divided by 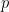 , and
, and 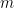
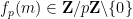 expansion of
expansion of 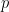 :
: 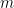
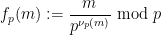 (
(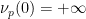 ).
).  In the case of
In the case of 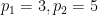
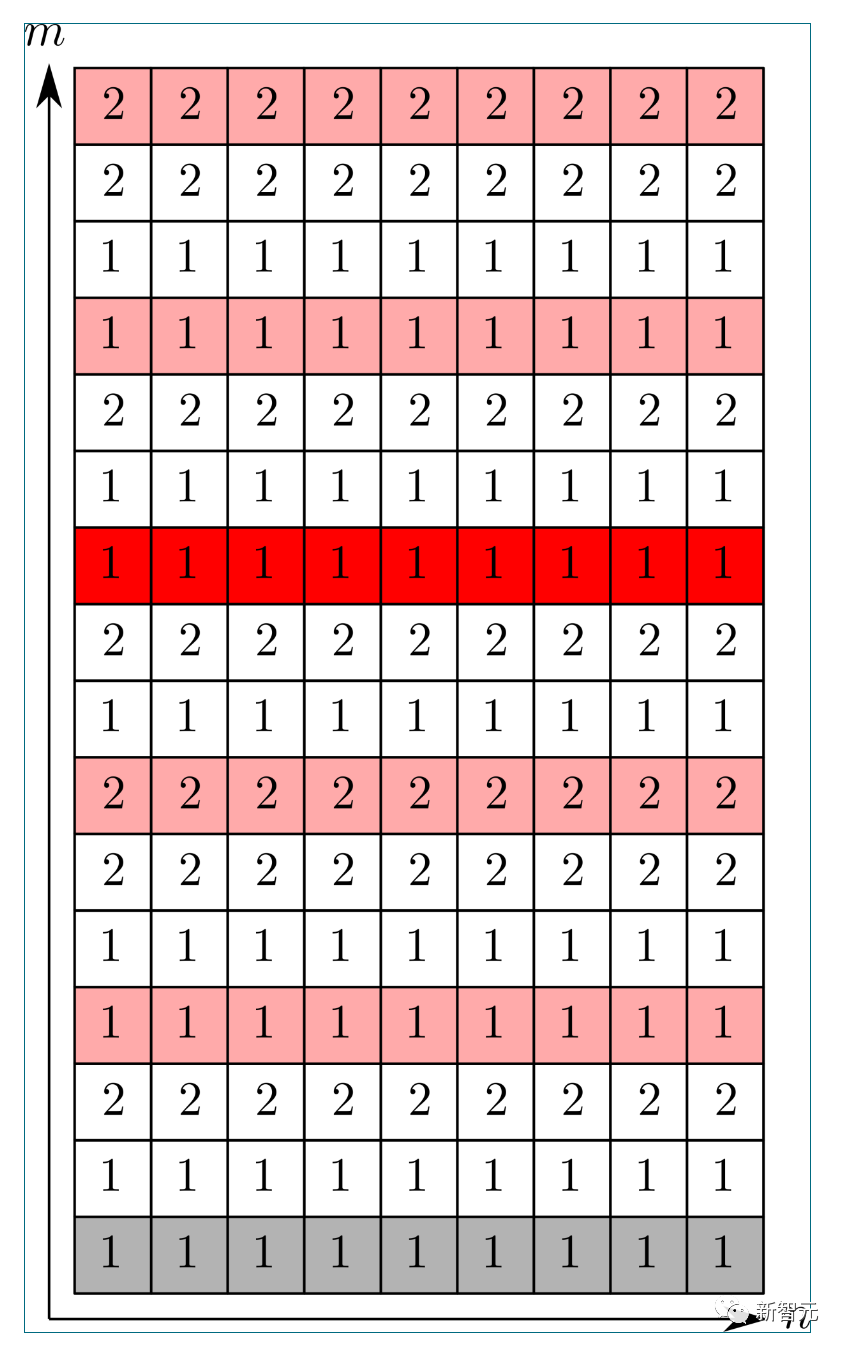 A typical example of the final component
A typical example of the final component 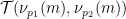
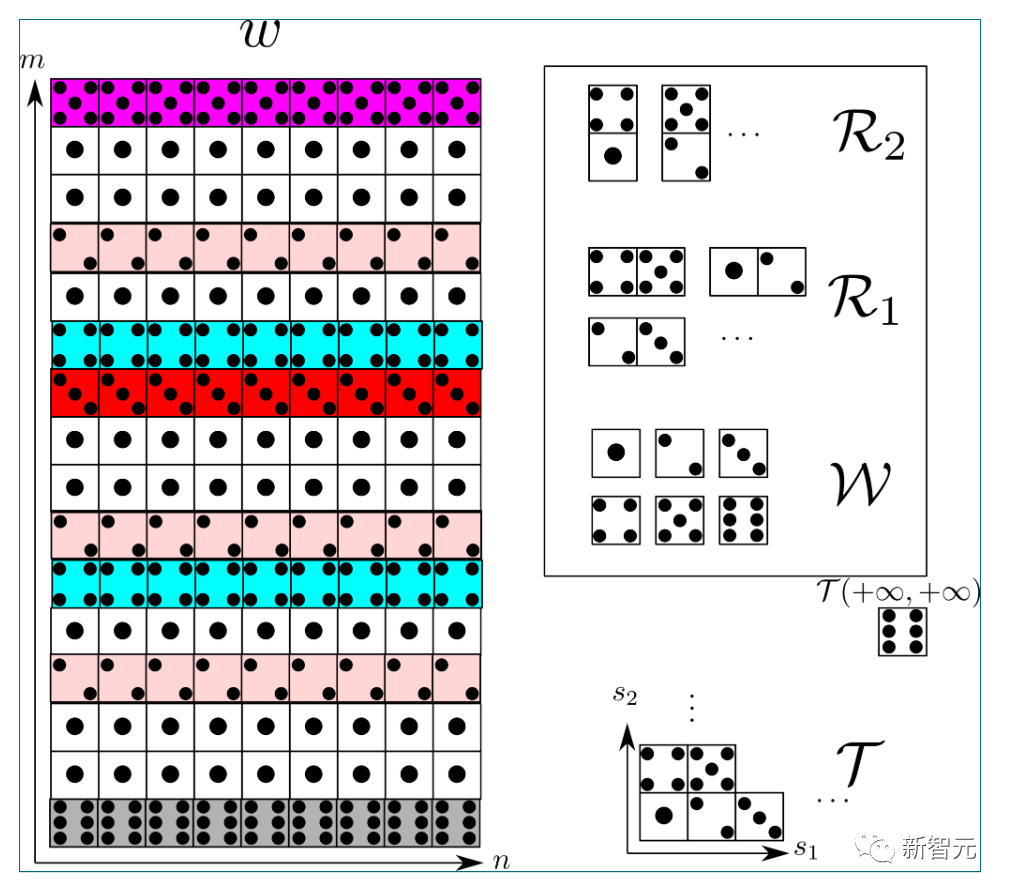 Interesting Yes, I don’t know why, but the decoration here basically follows the rules of the children’s game “Fizz Buzz”
Interesting Yes, I don’t know why, but the decoration here basically follows the rules of the children’s game “Fizz Buzz”
The above is the detailed content of Terence Tao approaches another 60-year geometry problem! A new breakthrough has been made in the problem of periodic close paving. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
 heptagon number
Sep 24, 2023 am 10:33 AM
heptagon number
Sep 24, 2023 am 10:33 AM
Aheptagonalnumberisanumberwhichcanberepresentedasaheptagon.Aheptagonisapolygonwith7sides.Aheptagonalnumbercanberepresentedasacombinationofsuccessivelayersofheptagon(7-sidedpolygon).Heptagonalnumbercanbebetterexplainedwiththebelowfigures. therefore,
 Groundbreaking CVM algorithm solves more than 40 years of counting problems! Computer scientist flips coin to figure out unique word for 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Groundbreaking CVM algorithm solves more than 40 years of counting problems! Computer scientist flips coin to figure out unique word for 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Counting sounds simple, but in practice it is very difficult. Imagine you are transported to a pristine rainforest to conduct a wildlife census. Whenever you see an animal, take a photo. Digital cameras only record the total number of animals tracked, but you are interested in the number of unique animals, but there is no statistics. So what's the best way to access this unique animal population? At this point, you must be saying, start counting now and finally compare each new species from the photo to the list. However, this common counting method is sometimes not suitable for information amounts up to billions of entries. Computer scientists from the Indian Statistical Institute, UNL, and the National University of Singapore have proposed a new algorithm - CVM. It can approximate the calculation of different items in a long list.
 MLP was killed overnight! MIT Caltech and other revolutionary KANs break records and discover mathematical theorems that crush DeepMind
May 06, 2024 pm 03:10 PM
MLP was killed overnight! MIT Caltech and other revolutionary KANs break records and discover mathematical theorems that crush DeepMind
May 06, 2024 pm 03:10 PM
Overnight, the machine learning paradigm is about to change! Today, the infrastructure that dominates the field of deep learning is the multilayer perceptron (MLP), which places activation functions on neurons. So, beyond that, are there any new routes we can take? Just today, teams from MIT, Caltech, Northeastern University and other institutions released a new neural network structure-Kolmogorov–Arnold Networks (KAN). The researchers made a simple change to the MLP by moving the learnable activation function from the nodes (neurons) to the edges (weights)! Paper address: https://arxiv.org/pdf/2404.19756 This change seems baseless at first glance
 Does AI painting still need to know mathematics?
Jun 12, 2023 pm 02:05 PM
Does AI painting still need to know mathematics?
Jun 12, 2023 pm 02:05 PM
Vision With the development of artificial intelligence technology, AI painting has become a hot topic at the moment. By using deep learning algorithms, artificial intelligence can generate realistic images to create stunning works of art. Behind these amazing works, it is inseparable from the support of mathematical knowledge. Mathematical models play a vital role in AI painting. On the one hand, mathematical models are used to describe and represent image information, allowing computers to understand and process images. On the other hand, mathematical models are also used to train deep learning models to achieve automatic generation of images. Deep learning model brings high-quality image generation. Deep learning model is the core part of AI painting. It identifies and simulates the characteristics of images by learning a large amount of image data, and through multi-level data processing
 'Mathematical noob' ChatGPT understands human preferences very well! Generating random numbers online is the ultimate answer to the universe
Apr 01, 2023 am 11:48 AM
'Mathematical noob' ChatGPT understands human preferences very well! Generating random numbers online is the ultimate answer to the universe
Apr 01, 2023 am 11:48 AM
ChatGPT also understands human tricks when it comes to generating random numbers. ChatGPT may be a bullshit artist and a spreader of misinformation, but it is not a "mathematician"! Recently, Colin Fraser, a Meta data scientist, discovered that ChatGPT cannot generate truly random numbers, but is more like "human random numbers." Through experiments, Fraser concluded: "ChatGPT likes the numbers 42 and 7 very much." Netizens said that this means that humans like these numbers very much. ChatGPT also loves "The Ultimate Answer to the Universe". In his test, the prompt entered by Fraser is as follows: "Pick a random number
 Working during the day and doing research at night, Google Brain research scientists solved a conjecture that has puzzled the mathematical community for decades.
Apr 12, 2023 am 09:49 AM
Working during the day and doing research at night, Google Brain research scientists solved a conjecture that has puzzled the mathematical community for decades.
Apr 12, 2023 am 09:49 AM
In mid-October 2022, Justin Gilmer flew from California to New York to visit his former mentor Michael Saks, a mathematician at Rutgers University, on the East Coast. During the reminiscence, they did not talk about mathematics. In fact, Gilmer hasn’t thought seriously about math since earning his PhD at Rutgers University in 2015. At that time, he decided not to pursue a career in academia and began to teach himself programming. Over dinner with Saks, Gilmer told his mentor about his work at Google: machine learning and artificial intelligence. As he walked along the path on campus, Gilmer recalled that in 2013, he spent more than a year walking on this path.
 Is the mathematics behind the diffusion model too difficult to digest? Google makes it clear with a unified perspective
Apr 11, 2023 pm 07:46 PM
Is the mathematics behind the diffusion model too difficult to digest? Google makes it clear with a unified perspective
Apr 11, 2023 pm 07:46 PM
In recent times, AI painting has been very popular. While you are marveling at AI’s painting capabilities, what you may not know is that the diffusion model plays a big role in it. Take the popular model OpenAI's DALL·E 2 as an example. Just enter a simple text (prompt) and it can generate multiple 1024*1024 high-definition images. Not long after DALL·E 2 was announced, Google subsequently released Imagen, a text-to-image AI model that can generate realistic images of the scene from a given text description. Just a few days ago, Stability.Ai publicly released the text generation image model Stable Diffusi





