What is NeRF? Is NeRF-based 3D reconstruction voxel-based?
1 Introduction
Neural Radiation Fields (NeRF) are a fairly new paradigm in the field of deep learning and computer vision. The technique was introduced in the ECCV 2020 paper "NeRF: Representing Scenes as Neural Radiation Fields for View Synthesis" (which won the Best Paper Award), and has since exploded in popularity, with nearly 800 citations to date [ 1]. The approach marks a sea change in the traditional way machine learning processes 3D data.
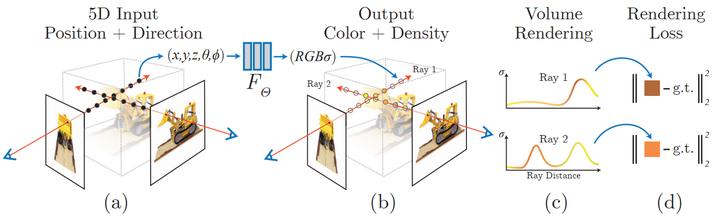
Neural radiation field scene representation and differentiable rendering process:
Synthesize the image by sampling 5D coordinates (position and viewing direction) along the camera ray; These locations are fed into an MLP to produce color and volumetric densities; and these values are composited into an image using volumetric rendering techniques; this rendering function is differentiable, so the scene can be optimized by minimizing the residual between the composite and real observed images express.
2 What is a NeRF?
NeRF is a generative model that generates new views of a 3D scene given an image, conditioned on an image and a precise pose. This process is often called for "New View Composition". Not only that, it also clearly defines the 3D shape and appearance of the scene as a continuous function, which can generate 3D meshes by marching cubes. Although they learn directly from image data, they use neither convolutional nor transformer layers.
Over the years, there have been many ways to represent 3D data in machine learning applications, from 3D voxels to point clouds to signed distance functions. Their biggest common disadvantage is the need to assume a 3D model in advance, either using tools such as photogrammetry or lidar to generate 3D data, or to hand-craft the 3D model. However, many types of objects, such as highly reflective objects, "grid-like" objects, or transparent objects, cannot be scanned at scale. 3D reconstruction methods also often suffer from reconstruction errors, which can lead to step effects or drift that affect model accuracy.
In contrast, NeRF is based on the concept of ray light fields. A light field is a function that describes how light transmission occurs throughout a 3D volume. It describes the direction in which a ray of light moves at each x = (x, y, z) coordinate in space and in each direction d, described as the θ and ξ angles or unit vectors. Together they form a 5D feature space that describes light transmission in a 3D scene. Inspired by this representation, NeRF attempts to approximate a function that maps from this space to a 4D space consisting of color c = (R, G, B) and density (density) σ, which can be thought of as this 5D coordinate space The possibility of the ray being terminated (e.g. by occlusion). Therefore, standard NeRF is a function of the form F: (x, d) -> (c, σ).
The original NeRF paper parameterized this function using a multilayer perceptron trained on a set of images with known poses. This is one method in a class of techniques called generalized scene reconstruction, which aims to describe 3D scenes directly from a collection of images. This approach has some very nice properties:
- Learn directly from the data
- Continuous representation of the scene allows for very thin and complex structures, such as leaves or meshes
- Implicit physical properties such as specularity and roughness
- Implicit rendering of lighting in the scene
Since then, a series of improvement papers have emerged, for example, less Lens and single-lens learning [2, 3], support for dynamic scenes [4, 5], generalization of light fields to feature fields [6], learning from uncalibrated image collections on the network [7], combined with lidar data [8], large-scale scene representation [9], learning without neural networks [10], and so on.
3 NeRF Architecture
Overall, given a trained NeRF model and a camera with known pose and image dimensions, we build the scene through the following process:
- For each pixel, shoot a ray from the camera optical center through the scene to collect a set of samples at the (x, d) position
- Using the point of each sample and the view direction (x, d) d) as input to produce the output (c, σ) value (rgbσ)
- Using classic volume rendering techniques to construct the image
Light emission field (many documents translate it as "radiation Field" (but the translator thinks "Light Shooting Field" is more intuitive) function is just one of several components that, once combined, can create the visual effects seen in the video before. Overall, this article includes the following parts:
- Positional encoding
- Light field function approximator (MLP)
- Differentiable body Renderer (Differentiable volume renderer)
- Stratified Sampling Hierarchical Volume Sampling
In order to explain it with maximum clarity, this article lists the key elements of each component as Show code as concisely as possible. Reference is made to the original implementation of bmild and the PyTorch implementation of yenchenlin and krrish94.
3.1 Positional Encoder
Like the transformer model [11] introduced in 2017, NeRF also benefits from a positional encoder as its input. It uses high-frequency functions to map its continuous inputs into a higher-dimensional space to help the model learn high-frequency changes in the data, resulting in a cleaner model. This method circumvents the bias of the neural network on low-frequency functions, allowing NeRF to represent clearer details. The author refers to a paper on ICML 2019 [12].
If you are familiar with transformerd's positional encoding, the related implementation of NeRF is pretty standard, with the same alternating sine and cosine expressions. Position encoder implementation:
1 |
|
Thinking: This position encoding encodes input points. Is this input point a sampling point on the line of sight? Or a different viewing angle? Is self.n_freqs the sampling frequency on the line of sight? From this understanding, it should be the sampling position on the line of sight, because if the sampling position on the line of sight is not encoded, these positions cannot be effectively represented, and their RGBA cannot be trained.
3.2 Radiance Field Function
In the original text, the light field function is represented by the NeRF model. The NeRF model is a typical multi-layer perceptron, using encoded 3D points and viewing direction as takes input and returns an RGBA value as output. Although this article uses neural networks, any function approximator can be used here. For example, Yu et al.’s follow-up paper Plenoxels uses spherical harmonics to achieve orders of magnitude faster training while achieving competitive results [10].
 Picture
Picture
The NeRF model is 8 layers deep and the feature dimension of most layers is 256. The remaining connections are placed at layer 4. After these layers, RGB and σ values are generated. The RGB values are further processed with a linear layer, then concatenated with the viewing direction, then passed through another linear layer, and finally recombined with σ at the output. PyTorch module implementation of NeRF model:
1 |
|
Thinking: What are the input and output of this NERF class? What happens through this class? It can be seen from the __init__ function parameters that it mainly sets the input, level and dimension of the neural network. 5D data is input, that is, the viewpoint position and line of sight direction, and the output is RGBA. Question, is the output RGBA one point? Or is it a series of lines of sight? If it is a series, I have not seen how the position coding determines the RGBA of each sampling point?
I have not seen any explanation of the sampling interval; if it is a point, then which point on the line of sight is this RGBA? of? Is it the point RGBA that is the result of a collection of sight sampling points seen by the eyes? It can be seen from the NERF class code that multi-layer feedforward training is mainly performed based on the viewpoint position and line of sight direction. The 5D viewpoint position and line of sight direction are input and the 4D RGBA is output.
3.3 Differentiable Volume Renderer(Differentiable Volume Renderer)
The RGBA output points are located in 3D space, so to synthesize them into images, you need to apply equations 1-3 in Section 4 of the paper Describe the volume integral. Essentially, a weighted summation of all samples along the line of sight of each pixel is performed to obtain an estimated color value for that pixel. Each RGB sample is weighted by its transparency alpha value: higher alpha values indicate a higher likelihood that the sampled area is opaque, and therefore points further along the ray are more likely to be occluded. The cumulative product operation ensures that these further points are suppressed.
Volume rendering output by the original NeRF model:
1 |
|
Question: What is the main function here? What was entered? What is output?
3.4 Stratified Sampling
The RGB value finally picked up by the camera is the accumulation of light samples along the line of sight passing through the pixel. The classic volume rendering method is to accumulate points along the line of sight, and then The points are integrated, and at each point the probability that the ray travels without hitting any particles is estimated. Therefore, each pixel needs to sample points along the ray passing through it. To best approximate the integral, their stratified sampling method uniformly divides the space into N bins and draws a sample uniformly from each bin. Instead of simply drawing samples at equal intervals, the stratified sampling method allows the model to sample in continuous space, thus conditioning the network to learn on continuous space.
 Picture
Picture
Hierarchical sampling implemented in PyTorch:
1 |
|
3.5 Hierarchical Volume Sampling
The radiation field is represented by two multi-layer perceptrons: one operates at a coarse level, encoding the broad structural properties of the scene; the other refines the details at a fine level, enabling thin and detailed structures such as meshes and branches. Complex structure. Furthermore, the samples they receive are different, with coarse models processing wide, mostly regularly spaced samples throughout the ray, while fine models honing in regions with strong priors to obtain salient information.
这种“珩磨”过程是通过层次体积采样流程完成的。3D空间实际上非常稀疏,存在遮挡,因此大多数点对渲染图像的贡献不大。因此,对具有对积分贡献可能性高的区域进行过采样(oversample)更有好处。他们将学习到的归一化权重应用于第一组样本,以在光线上创建PDF,然后再将inverse transform sampling应用于该PDF以收集第二组样本。该集合与第一集合相结合,并被馈送到精细网络以产生最终输出。
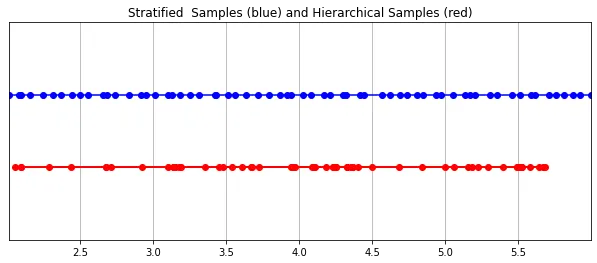
分层采样PyTorch实现:
1 |
|
训练
1 |
|
5 Conclusion
辐射场标志着处理3D数据的方式发生了巨大变化。NeRF模型和更广泛的可微分渲染正在迅速弥合图像创建和体积场景创建之间的差距。虽然我们的组件可能看起来非常复杂,但受vanilla NeRF启发的无数其他方法证明,基本概念(连续函数逼近器+可微分渲染器)是构建各种解决方案的坚实基础,这些解决方案可用于几乎无限的情况。
原文:NeRF From Nothing: A Tutorial with PyTorch | Towards Data Science
原文链接:https://mp.weixin.qq.com/s/zxJAIpAmLgsIuTsPqQqOVg
The above is the detailed content of What is NeRF? Is NeRF-based 3D reconstruction voxel-based?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 1207
1207
 24
24
 The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Imagine an artificial intelligence model that not only has the ability to surpass traditional computing, but also achieves more efficient performance at a lower cost. This is not science fiction, DeepSeek-V2[1], the world’s most powerful open source MoE model is here. DeepSeek-V2 is a powerful mixture of experts (MoE) language model with the characteristics of economical training and efficient inference. It consists of 236B parameters, 21B of which are used to activate each marker. Compared with DeepSeek67B, DeepSeek-V2 has stronger performance, while saving 42.5% of training costs, reducing KV cache by 93.3%, and increasing the maximum generation throughput to 5.76 times. DeepSeek is a company exploring general artificial intelligence
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
 Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Written previously, today we discuss how deep learning technology can improve the performance of vision-based SLAM (simultaneous localization and mapping) in complex environments. By combining deep feature extraction and depth matching methods, here we introduce a versatile hybrid visual SLAM system designed to improve adaptation in challenging scenarios such as low-light conditions, dynamic lighting, weakly textured areas, and severe jitter. sex. Our system supports multiple modes, including extended monocular, stereo, monocular-inertial, and stereo-inertial configurations. In addition, it also analyzes how to combine visual SLAM with deep learning methods to inspire other research. Through extensive experiments on public datasets and self-sampled data, we demonstrate the superiority of SL-SLAM in terms of positioning accuracy and tracking robustness.
 Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
The performance of JAX, promoted by Google, has surpassed that of Pytorch and TensorFlow in recent benchmark tests, ranking first in 7 indicators. And the test was not done on the TPU with the best JAX performance. Although among developers, Pytorch is still more popular than Tensorflow. But in the future, perhaps more large models will be trained and run based on the JAX platform. Models Recently, the Keras team benchmarked three backends (TensorFlow, JAX, PyTorch) with the native PyTorch implementation and Keras2 with TensorFlow. First, they select a set of mainstream
 Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas officially enters the era of electric robots! Yesterday, the hydraulic Atlas just "tearfully" withdrew from the stage of history. Today, Boston Dynamics announced that the electric Atlas is on the job. It seems that in the field of commercial humanoid robots, Boston Dynamics is determined to compete with Tesla. After the new video was released, it had already been viewed by more than one million people in just ten hours. The old people leave and new roles appear. This is a historical necessity. There is no doubt that this year is the explosive year of humanoid robots. Netizens commented: The advancement of robots has made this year's opening ceremony look like a human, and the degree of freedom is far greater than that of humans. But is this really not a horror movie? At the beginning of the video, Atlas is lying calmly on the ground, seemingly on his back. What follows is jaw-dropping
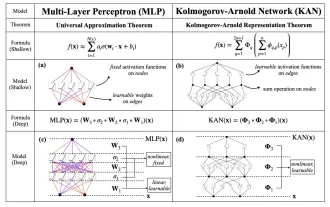 KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
Earlier this month, researchers from MIT and other institutions proposed a very promising alternative to MLP - KAN. KAN outperforms MLP in terms of accuracy and interpretability. And it can outperform MLP running with a larger number of parameters with a very small number of parameters. For example, the authors stated that they used KAN to reproduce DeepMind's results with a smaller network and a higher degree of automation. Specifically, DeepMind's MLP has about 300,000 parameters, while KAN only has about 200 parameters. KAN has a strong mathematical foundation like MLP. MLP is based on the universal approximation theorem, while KAN is based on the Kolmogorov-Arnold representation theorem. As shown in the figure below, KAN has
 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
Target detection is a relatively mature problem in autonomous driving systems, among which pedestrian detection is one of the earliest algorithms to be deployed. Very comprehensive research has been carried out in most papers. However, distance perception using fisheye cameras for surround view is relatively less studied. Due to large radial distortion, standard bounding box representation is difficult to implement in fisheye cameras. To alleviate the above description, we explore extended bounding box, ellipse, and general polygon designs into polar/angular representations and define an instance segmentation mIOU metric to analyze these representations. The proposed model fisheyeDetNet with polygonal shape outperforms other models and simultaneously achieves 49.5% mAP on the Valeo fisheye camera dataset for autonomous driving
 Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
The latest video of Tesla's robot Optimus is released, and it can already work in the factory. At normal speed, it sorts batteries (Tesla's 4680 batteries) like this: The official also released what it looks like at 20x speed - on a small "workstation", picking and picking and picking: This time it is released One of the highlights of the video is that Optimus completes this work in the factory, completely autonomously, without human intervention throughout the process. And from the perspective of Optimus, it can also pick up and place the crooked battery, focusing on automatic error correction: Regarding Optimus's hand, NVIDIA scientist Jim Fan gave a high evaluation: Optimus's hand is the world's five-fingered robot. One of the most dexterous. Its hands are not only tactile




