 Technology peripherals
Technology peripherals
 AI
AI
 Terence Tao's Crazy Amway Copilot: It helped me complete a one-page proof and even guessed my subsequent process
Terence Tao's Crazy Amway Copilot: It helped me complete a one-page proof and even guessed my subsequent process
Terence Tao's Crazy Amway Copilot: It helped me complete a one-page proof and even guessed my subsequent process
After being “endorsed” by GPT-4, Copilot was also ambushed by Terence Tao.
He bluntly said that when programming, Copilot can directly predict what he will do next.
With Copilot, research has become more convenient, and Tao Zhexuan also used it to assist him in completing his latest research results.

Tao Zhexuan said that this part of the paper actually only has one page.
But to complete this one-page proof, he wrote more than 200 lines of code, using the newly learned programming language Lean4.

The GitHub page of Tao Zhexuan’s public code shows that Copilot has increased the speed of writing code by more than half.
Tao Zhexuan said that the reason why he chose Lean4 was because of its "rewriting strategy", which is to perform targeted partial replacement of a long expression.
For example, if a complex function f(x) is defined, when we want to enter the expression of f(114514), we can directly "rewrite" x into 114514 using code.
Tao Zhexuan said that this feature is not too convenient compared to LaTeX which requires repeated input of formulas.
So what new results has Tao Zhexuan’s “one-page proof” brought us this time?
One-page proof of new inequalities
This paper talks about issues related to MacLaughlin's inequality.
McLaughlin's inequality is a classic inequality in mathematics. It is derived based on the law that "the arithmetic mean of non-negative real numbers is greater than or equal to the geometric mean". It can be expressed as:
Assume y1…yn is a non-negative real number. For k=1…n, the mean Sk is defined as (the number of terms whose denominator is the numerator):

#It occurs as the normalized coefficient of a polynomial of degree n with roots.

(Remember this formula, we call it Formula 1)
Then MacLaughlin’s inequality can be expressed as:
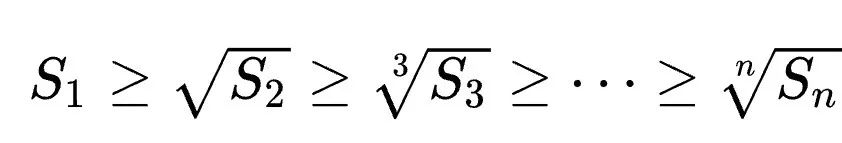
Among them, the equal sign holds true if and only if all yi are equal.
In calculus, there is also a classic Newton's inequality:
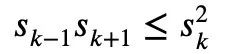
For any 1≤k
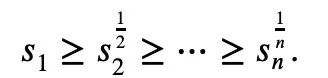
But if this restriction is not added, negative numbers are allowed With the existence of terms, Maclaurin's inequality cannot be expressed using Newton's inequality.
So for the situation where negative terms may exist in Newton's inequalities, Tao Zhexuan proposed a new set of inequality variants:
For any r>0 and 1≤ℓ≤n, there must be a formula 2 or Equation 3 is established.

This is what Terence Tao is trying to prove on this page. The specific proof process is as follows:
We might as well construct a polynomial about the complex variable z P(z):
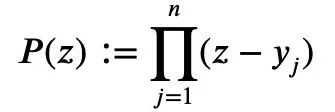
From the previous equation 1 and the triangle inequality, we can get:
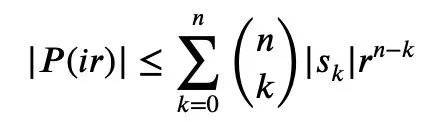
So we only need to establish the lower bound:
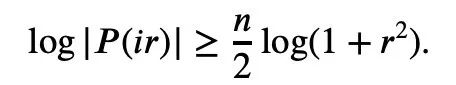
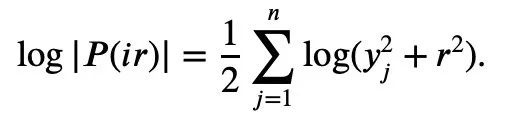
t a) is convex and a>0, we can get the inequality:
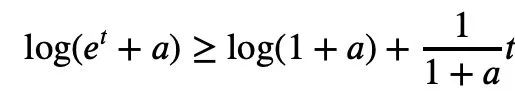
2, t=2log yj, it can be concluded:
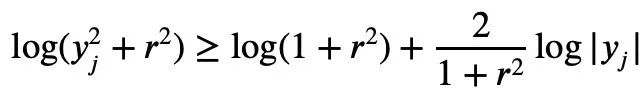
n|=1, the following formula holds:
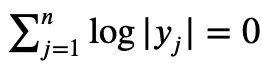
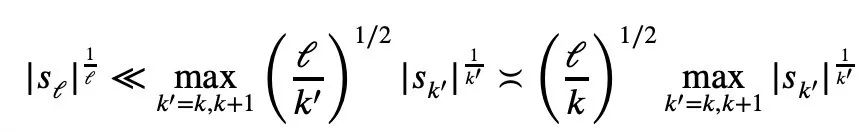


Paper address: https://arxiv.org/abs/2310.05328
The above is the detailed content of Terence Tao's Crazy Amway Copilot: It helped me complete a one-page proof and even guessed my subsequent process. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1359
1359
 52
52
 What method is used to convert strings into objects in Vue.js?
Apr 07, 2025 pm 09:39 PM
What method is used to convert strings into objects in Vue.js?
Apr 07, 2025 pm 09:39 PM
When converting strings to objects in Vue.js, JSON.parse() is preferred for standard JSON strings. For non-standard JSON strings, the string can be processed by using regular expressions and reduce methods according to the format or decoded URL-encoded. Select the appropriate method according to the string format and pay attention to security and encoding issues to avoid bugs.
 How to optimize database performance after mysql installation
Apr 08, 2025 am 11:36 AM
How to optimize database performance after mysql installation
Apr 08, 2025 am 11:36 AM
MySQL performance optimization needs to start from three aspects: installation configuration, indexing and query optimization, monitoring and tuning. 1. After installation, you need to adjust the my.cnf file according to the server configuration, such as the innodb_buffer_pool_size parameter, and close query_cache_size; 2. Create a suitable index to avoid excessive indexes, and optimize query statements, such as using the EXPLAIN command to analyze the execution plan; 3. Use MySQL's own monitoring tool (SHOWPROCESSLIST, SHOWSTATUS) to monitor the database health, and regularly back up and organize the database. Only by continuously optimizing these steps can the performance of MySQL database be improved.
 Laravel's geospatial: Optimization of interactive maps and large amounts of data
Apr 08, 2025 pm 12:24 PM
Laravel's geospatial: Optimization of interactive maps and large amounts of data
Apr 08, 2025 pm 12:24 PM
Efficiently process 7 million records and create interactive maps with geospatial technology. This article explores how to efficiently process over 7 million records using Laravel and MySQL and convert them into interactive map visualizations. Initial challenge project requirements: Extract valuable insights using 7 million records in MySQL database. Many people first consider programming languages, but ignore the database itself: Can it meet the needs? Is data migration or structural adjustment required? Can MySQL withstand such a large data load? Preliminary analysis: Key filters and properties need to be identified. After analysis, it was found that only a few attributes were related to the solution. We verified the feasibility of the filter and set some restrictions to optimize the search. Map search based on city
 How to solve mysql cannot be started
Apr 08, 2025 pm 02:21 PM
How to solve mysql cannot be started
Apr 08, 2025 pm 02:21 PM
There are many reasons why MySQL startup fails, and it can be diagnosed by checking the error log. Common causes include port conflicts (check port occupancy and modify configuration), permission issues (check service running user permissions), configuration file errors (check parameter settings), data directory corruption (restore data or rebuild table space), InnoDB table space issues (check ibdata1 files), plug-in loading failure (check error log). When solving problems, you should analyze them based on the error log, find the root cause of the problem, and develop the habit of backing up data regularly to prevent and solve problems.
 The primary key of mysql can be null
Apr 08, 2025 pm 03:03 PM
The primary key of mysql can be null
Apr 08, 2025 pm 03:03 PM
The MySQL primary key cannot be empty because the primary key is a key attribute that uniquely identifies each row in the database. If the primary key can be empty, the record cannot be uniquely identifies, which will lead to data confusion. When using self-incremental integer columns or UUIDs as primary keys, you should consider factors such as efficiency and space occupancy and choose an appropriate solution.
 Vue and Element-UI cascade drop-down box v-model binding
Apr 07, 2025 pm 08:06 PM
Vue and Element-UI cascade drop-down box v-model binding
Apr 07, 2025 pm 08:06 PM
Vue and Element-UI cascaded drop-down boxes v-model binding common pit points: v-model binds an array representing the selected values at each level of the cascaded selection box, not a string; the initial value of selectedOptions must be an empty array, not null or undefined; dynamic loading of data requires the use of asynchronous programming skills to handle data updates in asynchronously; for huge data sets, performance optimization techniques such as virtual scrolling and lazy loading should be considered.
 Vue.js How to convert an array of string type into an array of objects?
Apr 07, 2025 pm 09:36 PM
Vue.js How to convert an array of string type into an array of objects?
Apr 07, 2025 pm 09:36 PM
Summary: There are the following methods to convert Vue.js string arrays into object arrays: Basic method: Use map function to suit regular formatted data. Advanced gameplay: Using regular expressions can handle complex formats, but they need to be carefully written and considered. Performance optimization: Considering the large amount of data, asynchronous operations or efficient data processing libraries can be used. Best practice: Clear code style, use meaningful variable names and comments to keep the code concise.
 How to use mysql after installation
Apr 08, 2025 am 11:48 AM
How to use mysql after installation
Apr 08, 2025 am 11:48 AM
The article introduces the operation of MySQL database. First, you need to install a MySQL client, such as MySQLWorkbench or command line client. 1. Use the mysql-uroot-p command to connect to the server and log in with the root account password; 2. Use CREATEDATABASE to create a database, and USE select a database; 3. Use CREATETABLE to create a table, define fields and data types; 4. Use INSERTINTO to insert data, query data, update data by UPDATE, and delete data by DELETE. Only by mastering these steps, learning to deal with common problems and optimizing database performance can you use MySQL efficiently.



