
After trying GPT-4, Tao Zhexuan used Github Copilot again.
This time, his trial scenario was to learn the Lean language and use it to formalize mathematical theorems.

# For large models, formal theorem proof is also a challenge. A formal proof is essentially a computer program, but unlike traditional programs in C or Python, the correctness of the proof can be verified using proof assistants such as the Lean language. Theorem proving is a special form of code generation that is very strict in its evaluation and leaves no room for illusions in the model.
The theorem mentioned by Terence Tao comes from a paper on October 9th:

The proof in the paper is less than one page, but Terence Tao's formal proof uses 200 lines of Lean language.
For example, in the paper, Tao Zhexuan just asserts that for any a>0,  is convex in real numbers, because this is a regular calculus exercise, and then calls Jensen's inequality , but it took about 50 lines of code to write out all the details.
is convex in real numbers, because this is a regular calculus exercise, and then calls Jensen's inequality , but it took about 50 lines of code to write out all the details.
Tao Zhexuan said that Github copilot's ability to correctly predict multiple lines of code for various routine verifications and infer the direction he wants from clues such as the names of theorems is "incredible".
Lean's "rewrite" strategy is indispensable, allowing you to modify lengthy assumptions or goals through targeted substitutions that operate on the expression without having to type it in its entirety.
"When writing proofs in LaTeX, I often roughly simulate this method by cutting and pasting the lengthy expression I want to work with from one line to the next and then editing it accordingly, but this This sometimes causes typos to spread across multiple lines in the document, so it is good to be able to rewrite it in an automatic and verifiable way."
The paper also mentioned an inequality, that is, for any k, l, n satisfies  , then
, then
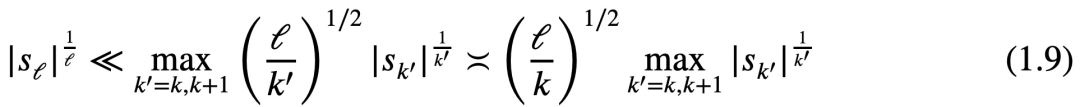 Tao Zhexuan said that the next goal is to establish a simple version of this inequality, that is, inequality (1.8) in the paper:
Tao Zhexuan said that the next goal is to establish a simple version of this inequality, that is, inequality (1.8) in the paper:

The proof in this part mainly uses the knowledge of calculus, but one difficulty is the need to use asymptotic symbols. Tao Zhexuan said that although the subsequent demonstration will be time-consuming, it is not particularly difficult.

The above is the detailed content of Tao Zhexuan gets started with Copilot: Incredible, it can guess the direction I want from the theorem name. For more information, please follow other related articles on the PHP Chinese website!




