
In machine learning, the term ensemble refers to combining multiple models in parallel. The idea is to use the wisdom of the crowd to form a better consensus on the final answer given.

In the field of supervised learning, this method has been widely studied and applied, especially in classification problems with very successful algorithms like RandomForest. A voting/weighting system is often employed to combine the output of each individual model into a more robust and consistent final output. In the world of unsupervised learning, this task becomes more difficult. First, because it encompasses the challenges of the field itself, we have no prior knowledge of the data to compare ourselves to any target. Second, because finding a suitable way to combine information from all models remains a problem, and there is no consensus on how to do this.
In this article, we discuss the best approach on this topic, namely clustering of similarity matrices.
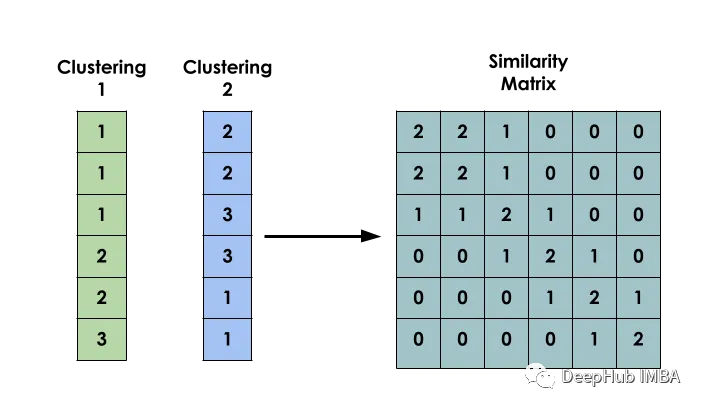 The main idea of this method is: given a data set X, create a matrix S such that Si represents the similarity between xi and xj. This matrix is constructed based on the clustering results of several different models.
The main idea of this method is: given a data set X, create a matrix S such that Si represents the similarity between xi and xj. This matrix is constructed based on the clustering results of several different models.
Binary co-occurrence matrix
 it Used to indicate whether two inputs i and j belong to the same cluster.
it Used to indicate whether two inputs i and j belong to the same cluster.
import numpy as np from scipy import sparse def build_binary_matrix( clabels ): data_len = len(clabels) matrix=np.zeros((data_len,data_len))for i in range(data_len):matrix[i,:] = clabels == clabels[i]return matrix labels = np.array( [1,1,1,2,3,3,2,4] ) build_binary_matrix(labels)
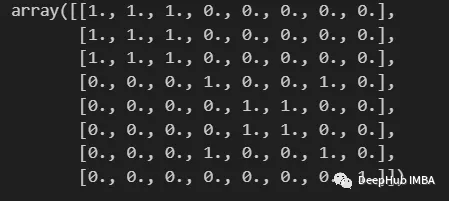 Use KMeans to construct a similarity matrix
Use KMeans to construct a similarity matrix
We introduce here a common method, which only involves calculating the average value between M co-occurrence matrices generated by M different models. We define it as:
 When the entries fall in the same cluster, their similarity value will be close to 1, while when the entries fall in different groups, Their similarity value will be close to 0
When the entries fall in the same cluster, their similarity value will be close to 1, while when the entries fall in different groups, Their similarity value will be close to 0
We will build a similarity matrix based on the labels created by the K-Means model. Conducted using the MNIST dataset. For simplicity and efficiency, we will only use 10,000 PCA-reduced images.
from sklearn.datasets import fetch_openml from sklearn.decomposition import PCA from sklearn.cluster import MiniBatchKMeans, KMeans from sklearn.model_selection import train_test_split mnist = fetch_openml('mnist_784') X = mnist.data y = mnist.target X, _, y, _ = train_test_split(X,y, train_size=10000, stratify=y, random_state=42 ) pca = PCA(n_components=0.99) X_pca = pca.fit_transform(X)To allow for diversity between models, each model is instantiated with a random number of clusters.
NUM_MODELS = 500 MIN_N_CLUSTERS = 2 MAX_N_CLUSTERS = 300 np.random.seed(214) model_sizes = np.random.randint(MIN_N_CLUSTERS, MAX_N_CLUSTERS+1, size=NUM_MODELS) clt_models = [KMeans(n_clusters=i, n_init=4, random_state=214) for i in model_sizes] for i, model in enumerate(clt_models):print( f"Fitting - {i+1}/{NUM_MODELS}" )model.fit(X_pca)The following function is to create a similarity matrix
def build_similarity_matrix( models_labels ):n_runs, n_data = models_labels.shape[0], models_labels.shape[1] sim_matrix = np.zeros( (n_data, n_data) ) for i in range(n_runs):sim_matrix += build_binary_matrix( models_labels[i,:] ) sim_matrix = sim_matrix/n_runs return sim_matrix
Call this function:
models_labels = np.array([ model.labels_ for model in clt_models ]) sim_matrix = build_similarity_matrix(models_labels)
The final result is as follows:
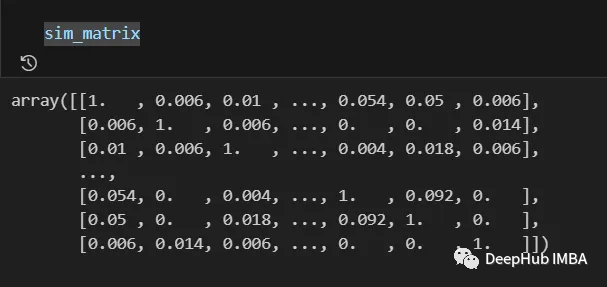 The information from the similarity matrix can still be post-processed before the last step, such as applying logarithmic, polynomial, etc. transformations.
The information from the similarity matrix can still be post-processed before the last step, such as applying logarithmic, polynomial, etc. transformations.
In our case, we will keep the original intention unchanged and rewrite
Pos_sim_matrix = sim_matrix
Clustering the similarity matrix
We can use it to visually see which entries are more likely to belong to the same cluster and which ones do not. However, this information still needs to be converted into actual clusters. This is done by using a clustering algorithm that can receive a similarity matrix as a parameter. Here we use SpectralClustering.
from sklearn.cluster import SpectralClustering spec_clt = SpectralClustering(n_clusters=10, affinity='precomputed',n_init=5, random_state=214) final_labels = spec_clt.fit_predict(pos_sim_matrix)
Comparison with the standard KMeans model
Let’s compare it with KMeans to confirm whether our method is effective.
from seaborn import heatmap import matplotlib.pyplot as plt def data_contingency_matrix(true_labels, pred_labels): fig, (ax) = plt.subplots(1, 1, figsize=(8,8)) n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels)label_names.sort() contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) heatmap(contingency_matrix.astype(int), ax=ax,annot=True, annot_kws={"fontsize":14}, fmt='d') ax.set_xlabel("Clusters", fontsize=18)ax.set_xticks( [i+0.5 for i in range(n_clusters)] )ax.set_xticklabels([i for i in range(n_clusters)], fontsize=14) ax.set_ylabel("Original classes", fontsize=18)ax.set_yticks( [i+0.5 for i in range(n_classes)] )ax.set_yticklabels(label_names, fontsize=14, va="center") ax.set_title("Contingency Matrix\n", ha='center', fontsize=20)from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_score def purity( true_labels, pred_labels ): n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels) purity_vector = np.zeros( (n_classes) )contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) purity_vector = np.max(contingency_matrix, axis=1)/np.sum(contingency_matrix, axis=1) print( f"Mean Class Purity - {np.mean(purity_vector):.2f}" ) for i, true_label in enumerate(label_names):print( f" {true_label} - {purity_vector[i]:.2f}" ) cluster_purity_vector = np.zeros( (n_clusters) )cluster_purity_vector = np.max(contingency_matrix, axis=0)/np.sum(contingency_matrix, axis=0) print( f"Mean Cluster Purity - {np.mean(cluster_purity_vector):.2f}" ) for i in range(n_clusters):print( f" {i} - {cluster_purity_vector[i]:.2f}" ) kmeans_model = KMeans(10, n_init=50, random_state=214) km_labels = kmeans_model.fit_predict(X_pca) data_contingency_matrix(y, km_labels) print( "Single KMeans NMI - ", normalized_mutual_info_score(y, km_labels) ) print( "Single KMeans ARI - ", adjusted_rand_score(y, km_labels) ) purity(y, km_labels)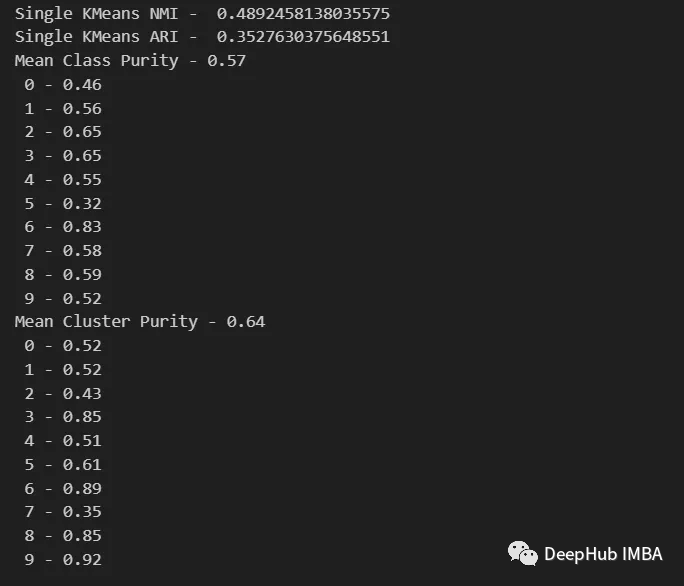
data_contingency_matrix(y, final_labels) print( "Ensamble NMI - ", normalized_mutual_info_score(y, final_labels) ) print( "Ensamble ARI - ", adjusted_rand_score(y, final_labels) ) purity(y, final_labels)
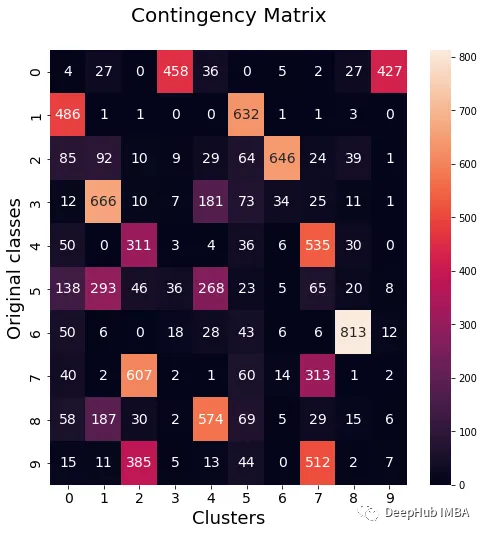
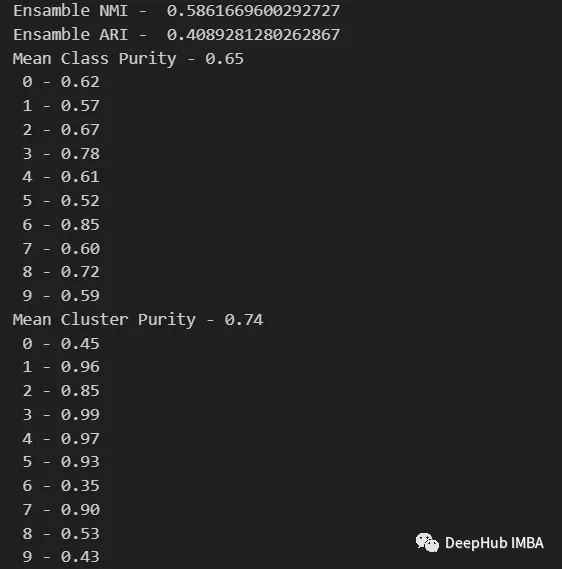
By observing the above values, it can be clearly seen that the Ensemble method can effectively improve the quality of clustering. At the same time, more consistent behavior can also be observed in the contingency matrix, with better distribution categories and less "noise"
The above is the detailed content of Ensemble methods for unsupervised learning: clustering of similarity matrices. For more information, please follow other related articles on the PHP Chinese website!




