 Technology peripherals
Technology peripherals
 AI
AI
 Princeton open source 34B mathematical model: parameters are halved, performance is comparable to Google Minerva, and 55 billion Tokens are used for professional data training
Princeton open source 34B mathematical model: parameters are halved, performance is comparable to Google Minerva, and 55 billion Tokens are used for professional data training
Princeton open source 34B mathematical model: parameters are halved, performance is comparable to Google Minerva, and 55 billion Tokens are used for professional data training
Mathematics, as the cornerstone of science, has always been a key area of research and innovation.
Recently, seven institutions including Princeton University jointly released a large language model LLEMMA specifically for mathematics, with performance comparable to Google Minerva 62B, and made its model, data set and code public , bringing unprecedented opportunities and resources to mathematical research.

Paper address: https://arxiv.org/abs/2310.10631
Dataset The link address is: https://huggingface.co/datasets/EleutherAI/proof-pile-2
Project address: https://github.com/EleutherAI/math-lm What needs to be rewritten is:
LLEMMA inherits the foundation of Code Llama and is pre-trained on Proof-Pile-2.
Proof-Pile-2, a huge mixed data set, contains information on 55 billion tokens, including scientific papers, web data rich in mathematical content, and mathematical codes.
Part of this data set, the Algebraic Stack, brings together 11B data sets from 17 languages, covering numerical, symbolic and mathematical proofs.
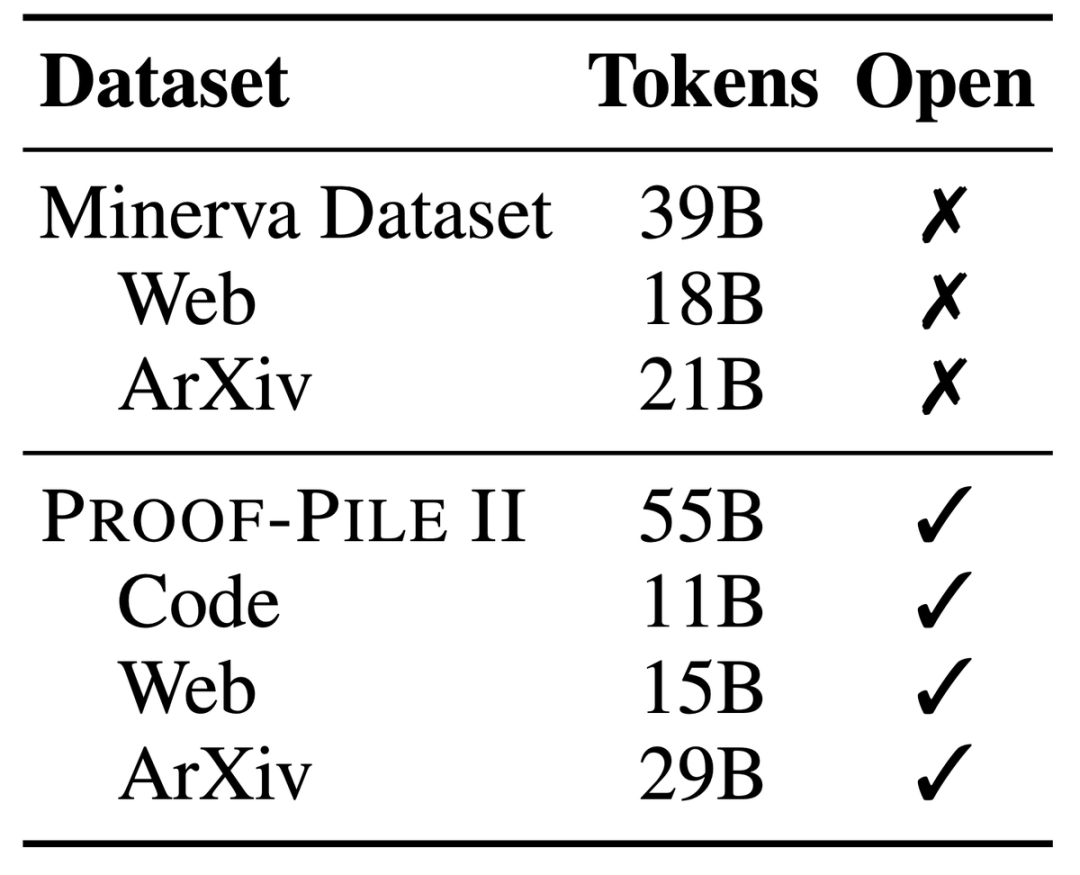
With 700 million and 3.4 billion parameters, it performs extremely well on the MATH benchmark, surpassing all known Open source base model.
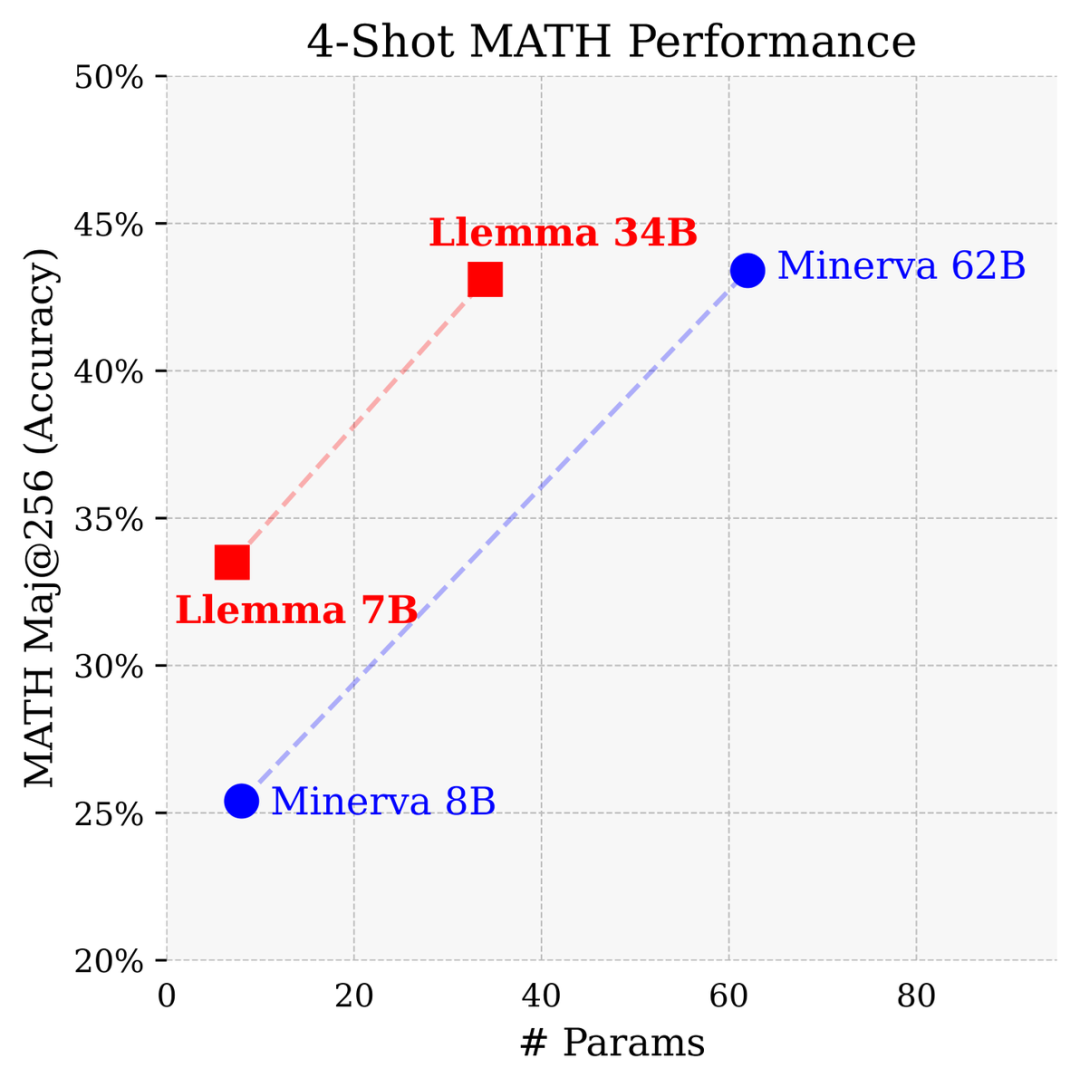
Compared with the closed model developed by Google Research specifically for mathematics, the number of parameters is only half of Minerva 62B Conditions, Llemma 34B achieved almost the same performance.
Llemma surpasses Minerva's performance in solving problems on a parametric basis. It uses computational tools and formal theorem proofs to provide unlimited possibilities for solving mathematical problems

It can conveniently use the Python interpreter and formal prover, further demonstrating its ability to solve mathematical problems
Due to special emphasis on formal proof data, Algebraic Stack has become the first open basic model to demonstrate the ability to prove few-sample theorem

 Figure
Figure
The researchers also openly shared all the training data and code of LLEMMA. Different from previous mathematical models, LLEMMA is an open source, open and shared model, opening the door to the entire scientific research community.
The researchers tried to quantify the model memory effect, and surprisingly, they found that Llemma did not become more accurate for problems that appeared in the training set. Because the code and data are publicly available, the researchers encourage others to replicate and extend their analysis
Training data and experimental configuration
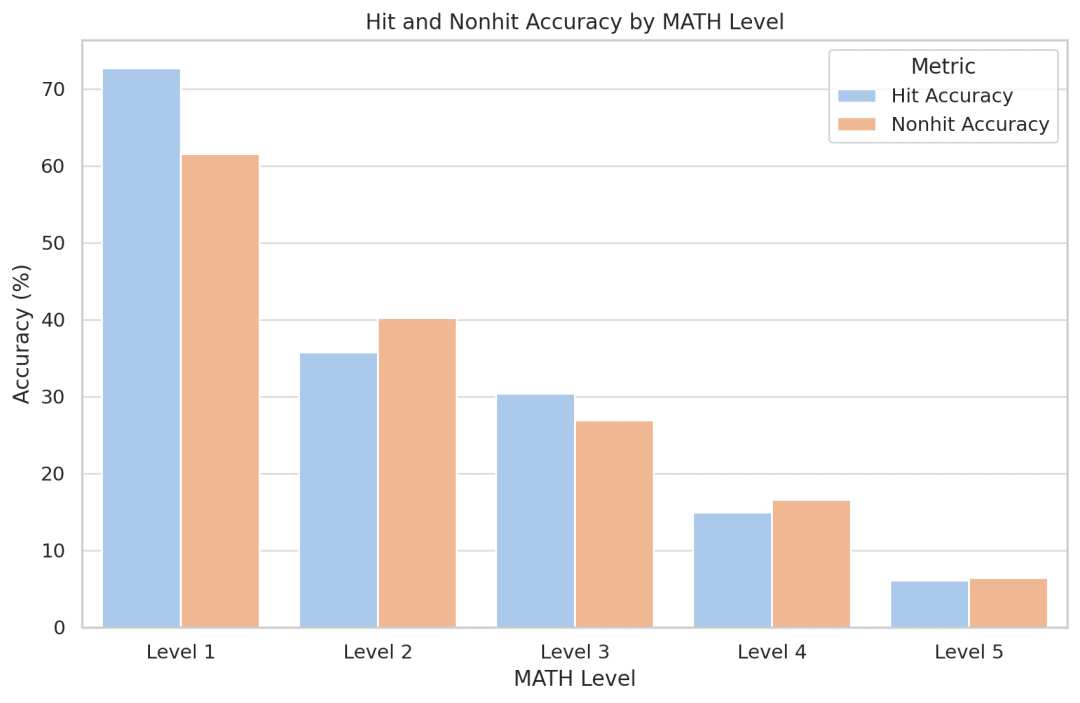
LLEMMA is a large language model dedicated to mathematics, which continues on the basis of Code Llama on Proof-Pile-2 Do pre-training. Proof-Pile-2 is a mixed dataset containing scientific papers, web data with mathematical content, and mathematical code. It contains 55 billion tags
The code part of AlgebraicStack contains 11B A dataset that includes source code in 17 languages, covering numerical, symbolic and formal mathematics, and has been publicly released for every model of
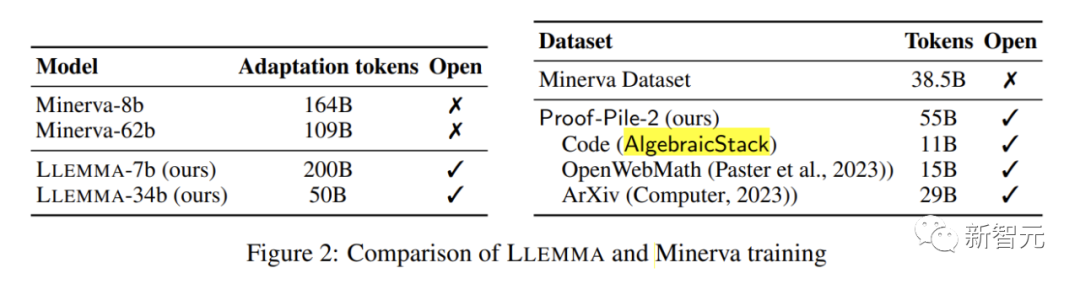
All are initialized by Code Llama. The Code Llama model is a decoder-only language model that is initialized from Llama 2
The author further trained the Code Llama model on Proof-Pile-2 , using standard autoregressive language modeling objectives. For the 7B model, the author performed training with 200B markers, while for the 34B model, the author performed training with 50B markers
Evaluation methods and experimental results
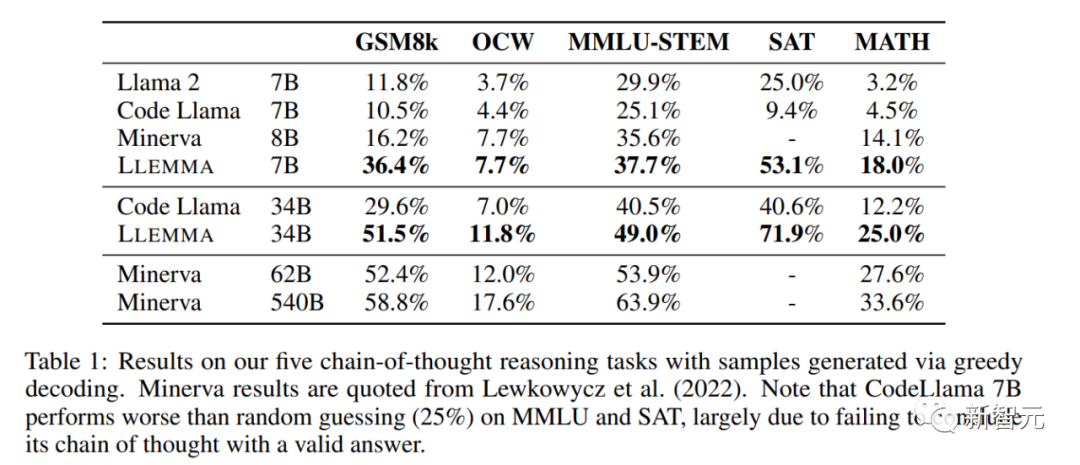
The author uses Proof-Pile-2 to continue pre-training Code Llama, and conducts a few-shot evaluation of LLEMMA on multiple mathematical problem solving tasks such as MATH and GSM8k.
The researchers found that LLEMMA significantly improved on these tasks and was able to adapt to different problem types and difficulties.
LLEMMA 34B demonstrates more powerful mathematical capabilities than other open-ended basic models in extremely difficult mathematical problems

On math benchmarks, LLEMMA’s continuous pre-training on Proof-Pile-2 improves few-shot performance on five math benchmarks.
The improvement of LLEMMA 34B is 20 percentage points higher than Code Llama on GSM8k and 13 percentage points higher on MATH. Moreover, LLEMMA 7B also outperforms the proprietary Minerva model of similar size, proving that pre-training on Proof-Pile-2 can effectively improve the mathematical problem-solving capabilities of large models
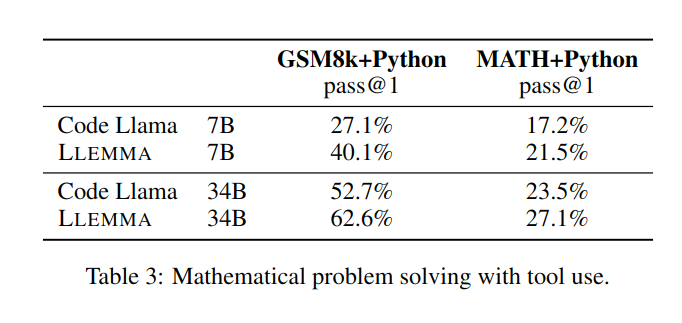
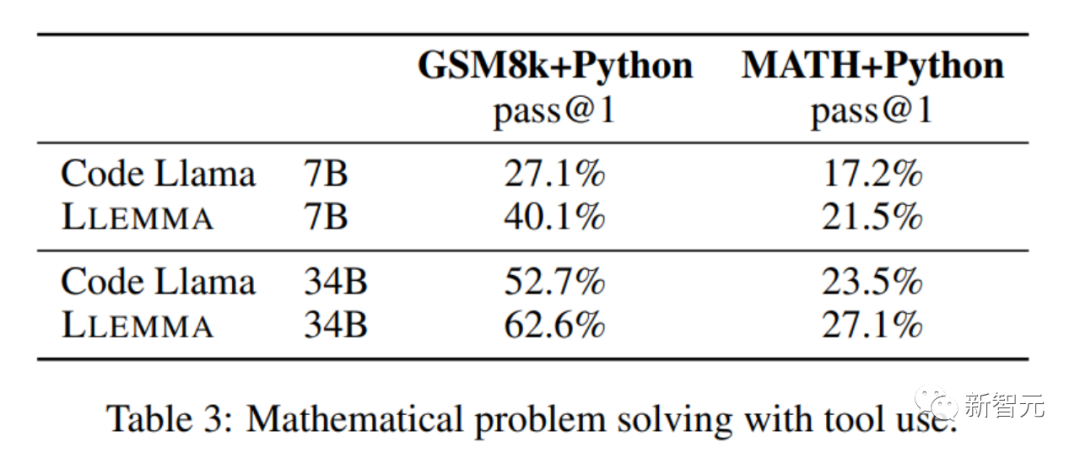
When solving mathematical problems, using computing tools such as Python, LLEMMA is better than Code Llama on both MATH Python and GSM8k Python tasks
When using MATH and GSM8k datasets, LLEMMA performs better than without the tool
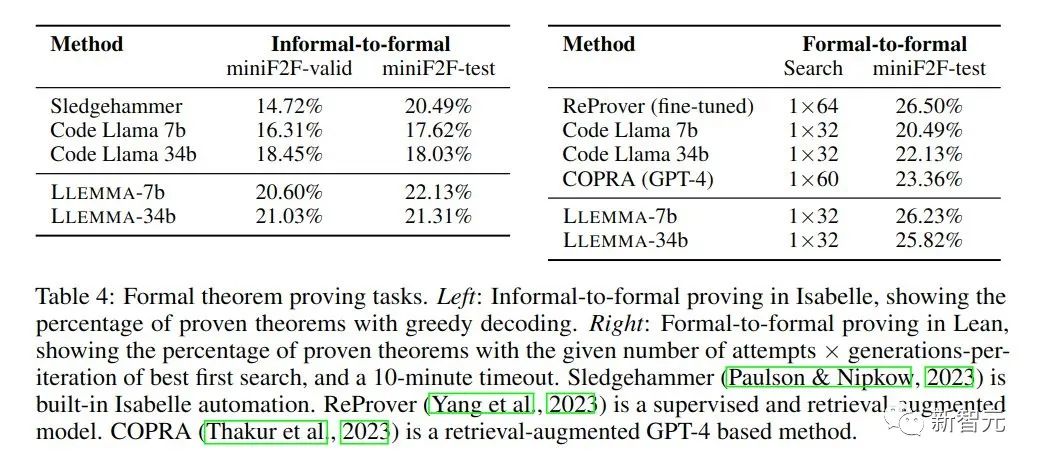
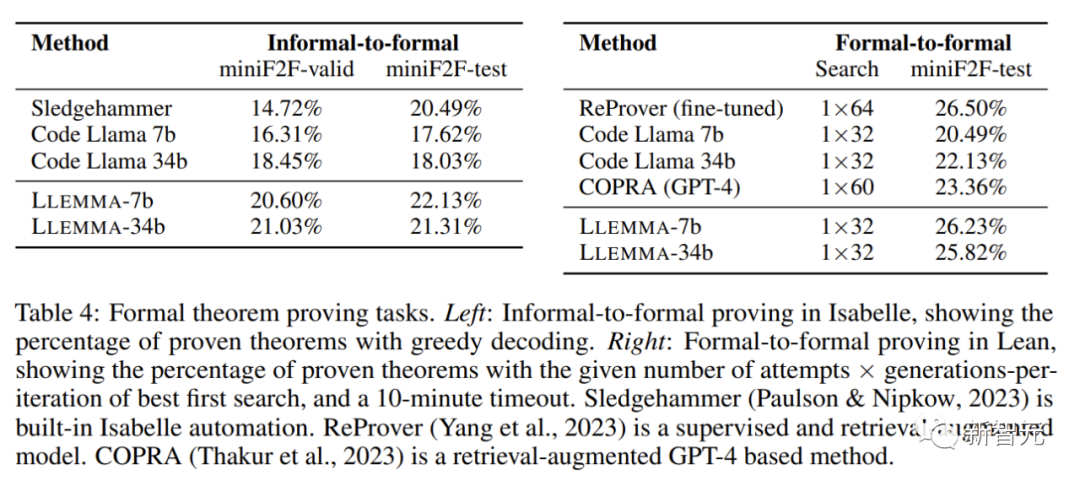
In mathematical proof tasks, LLEMMA performs well
The goal of the informal-to-formal proof task is to generate a formal proof, given a formal statement, an informal LATEX statement, and an informal LATEX proof, Then verify it through the proof assistant.
Formal to formal proof is to prove a formal statement by generating a series of proof steps (strategies). The results show that continuous pre-training of LLEMMA on Proof-Pile-2 improves the few-shot performance of these two formal theorem proving tasks.
LLEMMA not only has impressive performance, but also opens up revolutionary data sets and demonstrates amazing problem-solving capabilities.
The spirit of open source sharing marks the mathematical world entering a new era. The future of mathematics is here, and every one of us mathematics enthusiasts, researchers, and educators will benefit from it.
The emergence of LLEMMA provides us with unprecedented tools to make solving mathematical problems more efficient and innovative.
In addition, the concept of open sharing will also promote deeper cooperation among the global scientific research community and jointly promote scientific progress.
The above is the detailed content of Princeton open source 34B mathematical model: parameters are halved, performance is comparable to Google Minerva, and 55 billion Tokens are used for professional data training. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 Open source! Beyond ZoeDepth! DepthFM: Fast and accurate monocular depth estimation!
Apr 03, 2024 pm 12:04 PM
Open source! Beyond ZoeDepth! DepthFM: Fast and accurate monocular depth estimation!
Apr 03, 2024 pm 12:04 PM
0.What does this article do? We propose DepthFM: a versatile and fast state-of-the-art generative monocular depth estimation model. In addition to traditional depth estimation tasks, DepthFM also demonstrates state-of-the-art capabilities in downstream tasks such as depth inpainting. DepthFM is efficient and can synthesize depth maps within a few inference steps. Let’s read about this work together ~ 1. Paper information title: DepthFM: FastMonocularDepthEstimationwithFlowMatching Author: MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
 The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Imagine an artificial intelligence model that not only has the ability to surpass traditional computing, but also achieves more efficient performance at a lower cost. This is not science fiction, DeepSeek-V2[1], the world’s most powerful open source MoE model is here. DeepSeek-V2 is a powerful mixture of experts (MoE) language model with the characteristics of economical training and efficient inference. It consists of 236B parameters, 21B of which are used to activate each marker. Compared with DeepSeek67B, DeepSeek-V2 has stronger performance, while saving 42.5% of training costs, reducing KV cache by 93.3%, and increasing the maximum generation throughput to 5.76 times. DeepSeek is a company exploring general artificial intelligence
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
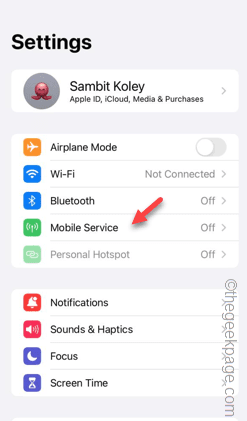 Slow Cellular Data Internet Speeds on iPhone: Fixes
May 03, 2024 pm 09:01 PM
Slow Cellular Data Internet Speeds on iPhone: Fixes
May 03, 2024 pm 09:01 PM
Facing lag, slow mobile data connection on iPhone? Typically, the strength of cellular internet on your phone depends on several factors such as region, cellular network type, roaming type, etc. There are some things you can do to get a faster, more reliable cellular Internet connection. Fix 1 – Force Restart iPhone Sometimes, force restarting your device just resets a lot of things, including the cellular connection. Step 1 – Just press the volume up key once and release. Next, press the Volume Down key and release it again. Step 2 – The next part of the process is to hold the button on the right side. Let the iPhone finish restarting. Enable cellular data and check network speed. Check again Fix 2 – Change data mode While 5G offers better network speeds, it works better when the signal is weaker
 Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas officially enters the era of electric robots! Yesterday, the hydraulic Atlas just "tearfully" withdrew from the stage of history. Today, Boston Dynamics announced that the electric Atlas is on the job. It seems that in the field of commercial humanoid robots, Boston Dynamics is determined to compete with Tesla. After the new video was released, it had already been viewed by more than one million people in just ten hours. The old people leave and new roles appear. This is a historical necessity. There is no doubt that this year is the explosive year of humanoid robots. Netizens commented: The advancement of robots has made this year's opening ceremony look like a human, and the degree of freedom is far greater than that of humans. But is this really not a horror movie? At the beginning of the video, Atlas is lying calmly on the ground, seemingly on his back. What follows is jaw-dropping
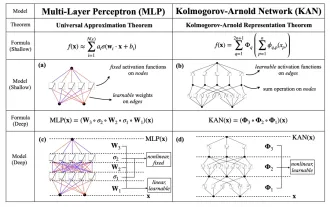 KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
Earlier this month, researchers from MIT and other institutions proposed a very promising alternative to MLP - KAN. KAN outperforms MLP in terms of accuracy and interpretability. And it can outperform MLP running with a larger number of parameters with a very small number of parameters. For example, the authors stated that they used KAN to reproduce DeepMind's results with a smaller network and a higher degree of automation. Specifically, DeepMind's MLP has about 300,000 parameters, while KAN only has about 200 parameters. KAN has a strong mathematical foundation like MLP. MLP is based on the universal approximation theorem, while KAN is based on the Kolmogorov-Arnold representation theorem. As shown in the figure below, KAN has
 The vitality of super intelligence awakens! But with the arrival of self-updating AI, mothers no longer have to worry about data bottlenecks
Apr 29, 2024 pm 06:55 PM
The vitality of super intelligence awakens! But with the arrival of self-updating AI, mothers no longer have to worry about data bottlenecks
Apr 29, 2024 pm 06:55 PM
I cry to death. The world is madly building big models. The data on the Internet is not enough. It is not enough at all. The training model looks like "The Hunger Games", and AI researchers around the world are worrying about how to feed these data voracious eaters. This problem is particularly prominent in multi-modal tasks. At a time when nothing could be done, a start-up team from the Department of Renmin University of China used its own new model to become the first in China to make "model-generated data feed itself" a reality. Moreover, it is a two-pronged approach on the understanding side and the generation side. Both sides can generate high-quality, multi-modal new data and provide data feedback to the model itself. What is a model? Awaker 1.0, a large multi-modal model that just appeared on the Zhongguancun Forum. Who is the team? Sophon engine. Founded by Gao Yizhao, a doctoral student at Renmin University’s Hillhouse School of Artificial Intelligence.
 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
Target detection is a relatively mature problem in autonomous driving systems, among which pedestrian detection is one of the earliest algorithms to be deployed. Very comprehensive research has been carried out in most papers. However, distance perception using fisheye cameras for surround view is relatively less studied. Due to large radial distortion, standard bounding box representation is difficult to implement in fisheye cameras. To alleviate the above description, we explore extended bounding box, ellipse, and general polygon designs into polar/angular representations and define an instance segmentation mIOU metric to analyze these representations. The proposed model fisheyeDetNet with polygonal shape outperforms other models and simultaneously achieves 49.5% mAP on the Valeo fisheye camera dataset for autonomous driving



