 Technology peripherals
Technology peripherals
 AI
AI
 The first LLM that supports 4-bit floating point quantization is here to solve the deployment problems of LLaMA, BERT, etc.
The first LLM that supports 4-bit floating point quantization is here to solve the deployment problems of LLaMA, BERT, etc.
The first LLM that supports 4-bit floating point quantization is here to solve the deployment problems of LLaMA, BERT, etc.
Large Language Model (LLM) compression has always attracted much attention. Post-training Quantization is one of the commonly used algorithms. However, most of the existing PTQ methods are integer quantization, and when the number of bits Below 8, the accuracy of the quantized model will drop significantly. Compared with Integer (INT) quantization, Floating Point (FP) quantization can better represent long-tail distributions, so more and more hardware platforms are beginning to support FP quantization. This article gives a solution to FP quantification of large models. Article published at EMNLP 2023.

- ##Paper address: https://arxiv.org/abs/2310.16836
- Code address: https://github.com/nbasyl/LLM-FP4
To understand this article, you must first Have basic knowledge about Floating Point Format and Floating Point Quantization. First, Floating Point Number can be expressed by the following formula:

s represents the sign bit, m represents the mantissa bits, and e represents the exponent bits. p is a value between 0 and 2^e - 1, used to indicate which exponential interval the current number should be divided into, d takes a value of 0 or 1, used to indicate the i-th mantissa bit. b is bias, an integer value used to adjust the exponent interval.
In the following sections, we will explain how floating point quantification works. First, the input values must go through a step called "scale and clip." This step first clips the input value to the maximum range that floating point numbers can represent (±Qmax). The specific calculation formula is as follows:

You can see that similar to integer quantization, FP quantization will also add a full-precision scaling factor to scale the input to an appropriate interval. When calculating matrix multiplication, the scaling factor is calculated separately from the low-bit matrix multiplication, so it does not cause a large overhead. After incorporating this full-precision scaling factor, different quantized tensors can be clipped to different maximum and minimum value intervals accordingly. In actual use, the required quantization interval will be determined based on the value range of the input tensor, and then the corresponding bias will be derived using formula (4). Note that bias in equation (4) can be used as a scaling factor for real values, see equation (2)(3).
The next step in floating-point quantization is to assign the values in the determined quantization interval to the corresponding quantization interval. This process is called comparison and quantization:

#The above figure intuitively illustrates the quantization process. The current input value is quantized into different quantization intervals after being compared with Formula 5.
After obtaining the quantized activation and weight, the scaling factor here is calculated first as mentioned before, and the following efficient matrix multiplication is achieved to complete the acceleration of matrix multiplication:

Then this article points out that the accuracy of FP quantization is closely related to the setting of exponent bits and the quantization interval.
In previous papers, it has been verified that there are huge differences in quantization errors between different FP formats (ie, exponent bit/mantissa bit settings of floating point numbers). Only when the appropriate FP format is chosen, FP quantization can represent long-tail distributions better than INT quantization
 #
#
This article proposes a solution, which is to use a search-based floating-point quantization algorithm to determine the most suitable exponent and mantissa bit settings for floating-point numbers and the corresponding quantization interval in a comprehensive search manner
In addition, in various types of Transformer models (Bert, LLaMA, ViT), there is another phenomenon that seriously affects the difficulty of quantification: that is, different channels in the activation of the model The order of magnitude difference between them is very large, while the order of magnitude between the same channels is very consistent. Previous studies LLM.int8 and SmoothQuant also found similar phenomena, but this article points out that this phenomenon not only exists in LLM, but also found similar activation distributions in other Transformer models (shown below, LLaMA, BERT and DeIT-S) Phenomenon:

As you can see from the figure, those abnormally large channels are much larger than the remaining channels, so in the process of quantifying the activation tensor , the quantization accuracy will be largely determined by these outliers, thereby suppressing the quantization range of other channel values, and ultimately reducing the overall impact on quantization accuracy. This will cause the final result of quantization to collapse, especially when the number of bits drops to a certain level. It is worth noting that only tensor-wise and token-wise quantization can extract the scaling factor during efficient matrix multipilication, while channel-wise quantization does not support efficient matrix multipilication, as shown in the figure below.

In order to simultaneously solve the problem and maintain efficient matrix multiplication, this paper uses a small amount of rectified data sets to pre-compute activations Maximum value for each channel and calculate the scaling factor. The scaling factor is then split into a real number for each tensor multiplied by a power of 2 for each channel. This power of 2 can be represented by the exponential deviation in FP. The entire process can be expressed by the following formula:

Further, after the calibration is completed, the per-channel exponent bias is It no longer changes, so it can be pre-computed together with weight quantization to integrate this per-channel exponent bias into the quantized weights to improve the quantization accuracy. The complete process is as follows:

After the pre-offset, the full-precision offset of each channel in the original activation function can be observed The position becomes a tensor-based real scaling factor, and the decomposed integer offset is moved to the position of the original integer offset in the weight. See Formula 4
for details. This method (pre-shifted exponent bias) can better improve the quantization accuracy while maintaining the principle of efficient matrix multiplication. The intuitive display of the method is as shown in the figure below:

Finally, this article shows the Floating Point Quantization (FPQ) method. On LLaMA, BERT and ViTs models, 4-bit quantization has achieved results far exceeding SOTA. In particular, this article shows that the 4-bit quantized LLaMA-13B model achieves an average score of 63.1 on the zero-shot inference task, which is only 5.8 points lower than the full precision model and has a higher smoothing amount than the previous SOTA method. 12.7, which is currently one of the few known feasible 4-bit quantization schemes.

The above is the detailed content of The first LLM that supports 4-bit floating point quantization is here to solve the deployment problems of LLaMA, BERT, etc.. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
Imagine an artificial intelligence model that not only has the ability to surpass traditional computing, but also achieves more efficient performance at a lower cost. This is not science fiction, DeepSeek-V2[1], the world’s most powerful open source MoE model is here. DeepSeek-V2 is a powerful mixture of experts (MoE) language model with the characteristics of economical training and efficient inference. It consists of 236B parameters, 21B of which are used to activate each marker. Compared with DeepSeek67B, DeepSeek-V2 has stronger performance, while saving 42.5% of training costs, reducing KV cache by 93.3%, and increasing the maximum generation throughput to 5.76 times. DeepSeek is a company exploring general artificial intelligence
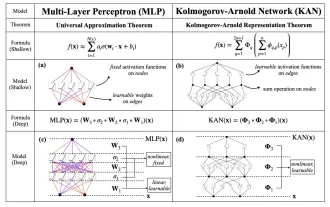 KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
Earlier this month, researchers from MIT and other institutions proposed a very promising alternative to MLP - KAN. KAN outperforms MLP in terms of accuracy and interpretability. And it can outperform MLP running with a larger number of parameters with a very small number of parameters. For example, the authors stated that they used KAN to reproduce DeepMind's results with a smaller network and a higher degree of automation. Specifically, DeepMind's MLP has about 300,000 parameters, while KAN only has about 200 parameters. KAN has a strong mathematical foundation like MLP. MLP is based on the universal approximation theorem, while KAN is based on the Kolmogorov-Arnold representation theorem. As shown in the figure below, KAN has
 Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas officially enters the era of electric robots! Yesterday, the hydraulic Atlas just "tearfully" withdrew from the stage of history. Today, Boston Dynamics announced that the electric Atlas is on the job. It seems that in the field of commercial humanoid robots, Boston Dynamics is determined to compete with Tesla. After the new video was released, it had already been viewed by more than one million people in just ten hours. The old people leave and new roles appear. This is a historical necessity. There is no doubt that this year is the explosive year of humanoid robots. Netizens commented: The advancement of robots has made this year's opening ceremony look like a human, and the degree of freedom is far greater than that of humans. But is this really not a horror movie? At the beginning of the video, Atlas is lying calmly on the ground, seemingly on his back. What follows is jaw-dropping
 Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
The performance of JAX, promoted by Google, has surpassed that of Pytorch and TensorFlow in recent benchmark tests, ranking first in 7 indicators. And the test was not done on the TPU with the best JAX performance. Although among developers, Pytorch is still more popular than Tensorflow. But in the future, perhaps more large models will be trained and run based on the JAX platform. Models Recently, the Keras team benchmarked three backends (TensorFlow, JAX, PyTorch) with the native PyTorch implementation and Keras2 with TensorFlow. First, they select a set of mainstream
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI is indeed changing mathematics. Recently, Tao Zhexuan, who has been paying close attention to this issue, forwarded the latest issue of "Bulletin of the American Mathematical Society" (Bulletin of the American Mathematical Society). Focusing on the topic "Will machines change mathematics?", many mathematicians expressed their opinions. The whole process was full of sparks, hardcore and exciting. The author has a strong lineup, including Fields Medal winner Akshay Venkatesh, Chinese mathematician Zheng Lejun, NYU computer scientist Ernest Davis and many other well-known scholars in the industry. The world of AI has changed dramatically. You know, many of these articles were submitted a year ago.
 Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
The latest video of Tesla's robot Optimus is released, and it can already work in the factory. At normal speed, it sorts batteries (Tesla's 4680 batteries) like this: The official also released what it looks like at 20x speed - on a small "workstation", picking and picking and picking: This time it is released One of the highlights of the video is that Optimus completes this work in the factory, completely autonomously, without human intervention throughout the process. And from the perspective of Optimus, it can also pick up and place the crooked battery, focusing on automatic error correction: Regarding Optimus's hand, NVIDIA scientist Jim Fan gave a high evaluation: Optimus's hand is the world's five-fingered robot. One of the most dexterous. Its hands are not only tactile
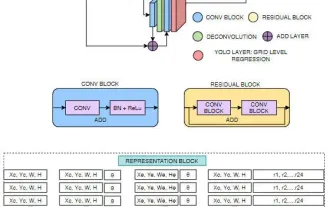 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
Target detection is a relatively mature problem in autonomous driving systems, among which pedestrian detection is one of the earliest algorithms to be deployed. Very comprehensive research has been carried out in most papers. However, distance perception using fisheye cameras for surround view is relatively less studied. Due to large radial distortion, standard bounding box representation is difficult to implement in fisheye cameras. To alleviate the above description, we explore extended bounding box, ellipse, and general polygon designs into polar/angular representations and define an instance segmentation mIOU metric to analyze these representations. The proposed model fisheyeDetNet with polygonal shape outperforms other models and simultaneously achieves 49.5% mAP on the Valeo fisheye camera dataset for autonomous driving
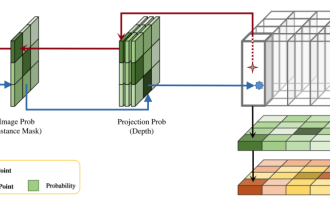 DualBEV: significantly surpassing BEVFormer and BEVDet4D, open the book!
Mar 21, 2024 pm 05:21 PM
DualBEV: significantly surpassing BEVFormer and BEVDet4D, open the book!
Mar 21, 2024 pm 05:21 PM
This paper explores the problem of accurately detecting objects from different viewing angles (such as perspective and bird's-eye view) in autonomous driving, especially how to effectively transform features from perspective (PV) to bird's-eye view (BEV) space. Transformation is implemented via the Visual Transformation (VT) module. Existing methods are broadly divided into two strategies: 2D to 3D and 3D to 2D conversion. 2D-to-3D methods improve dense 2D features by predicting depth probabilities, but the inherent uncertainty of depth predictions, especially in distant regions, may introduce inaccuracies. While 3D to 2D methods usually use 3D queries to sample 2D features and learn the attention weights of the correspondence between 3D and 2D features through a Transformer, which increases the computational and deployment time.





