 Technology peripherals
Technology peripherals
 AI
AI
 Exploring the History and Matrix of Artificial Intelligence: Artificial Intelligence Tutorial (2)
Exploring the History and Matrix of Artificial Intelligence: Artificial Intelligence Tutorial (2)
Exploring the History and Matrix of Artificial Intelligence: Artificial Intelligence Tutorial (2)

In the first article of this series, we discussed the connections and differences between artificial intelligence, machine learning, deep learning, data science and other fields. We also made some hard choices about the programming languages, tools, and more that the entire series would use. Finally, we also introduced a little bit of matrix knowledge. In this article, we will discuss in depth the matrix, the core of artificial intelligence. But before that, let’s first understand the history of artificial intelligence
Why do we need to understand the history of artificial intelligence? There have been many AI booms in history, but in many cases the huge expectations for AI's potential failed to materialize. Understanding the history of artificial intelligence can help us see whether this wave of artificial intelligence will create miracles or is just another bubble about to burst.
When did our understanding of the origin of artificial intelligence begin? Was it after the invention of the digital computer? Or earlier? I believe the pursuit of an omniscient being goes back to the beginning of civilization. For example, Delphi in ancient Greek mythology was a prophet who could answer any question. The search for creative machines that surpass human intelligence has also fascinated us since ancient times. There have been several failed attempts to build chess machines throughout history. Among them is the infamous Mechaturk, which is not a real robot but is controlled by a chess player hidden inside. The logarithms invented by John Napier, Blaise Pascal's calculator, and Charles Babbage's Analytical Engine all played a key role in the development of artificial intelligence
So, the development of artificial intelligence so far What are the milestones? As mentioned earlier, the invention of the digital computer is the most important event in the history of artificial intelligence research. Unlike electromechanical devices, whose scalability depends on power requirements, digital devices benefit from technological advances, such as from vacuum tubes to transistors to integrated circuits and now VLSI.
Another important milestone in the development of artificial intelligence is Alan Turing’s first theoretical analysis of artificial intelligence. He proposed the famous Turing Test
In the late 1950s, John McCarthy
By the 1970s and 1980s, algorithms played a major role in this period. During this time, many new efficient algorithms were proposed. In the late 1960s, Donald Knuth (I strongly recommend you to get to know him, in the computer science world, he is equivalent to Gauss or Euler in the mathematics world) famous "The Art of Computer Programming" The publication of the first volume of Programming marked the beginning of the algorithm era. During these years, many general-purpose algorithms and graph algorithms were developed. In addition, programming based on artificial neural networks also emerged at this time. Although as early as the 1940s, Warren S. McCulloch and Walter Pitts
artificial intelligence had at least two promising opportunities in the digital age, Both opportunities fell short of expectations. Is the current wave of artificial intelligence similar to this? This question is difficult to answer. However, I personally believe that artificial intelligence will have a huge impact this time (LCTT translation annotation: This article was published in June 2022, ChatGTP was launched half a year later). Why do I have such a prediction? First, high-performance computing equipment is now cheap and readily available. In the 1960s or 1980s, there were only a few such powerful computing devices, whereas now we have millions or even billions of them. Second, there is now a vast amount of data available for training artificial intelligence and machine learning programs. Imagine how many digital images engineers who were engaged in digital image processing in the 1990s could use to train algorithms? Maybe thousands or tens of thousands. Now, the data science platform Kaggle (a subsidiary of Google) alone has more than 10,000 data sets. The vast amount of data generated by the Internet every day makes it easier to train algorithms. Third, high-speed Internet connections make it easier to work with large institutions. In the first decade of the 21st century, collaboration among computer scientists was difficult. However, the speed of the Internet now makes collaboration with artificial intelligence projects such as Google Colab, Kaggle, and Project Jupiter a reality. Based on these three factors, I believe that artificial intelligence will exist forever this time, and there will be many excellent applications
More matrix knowledge
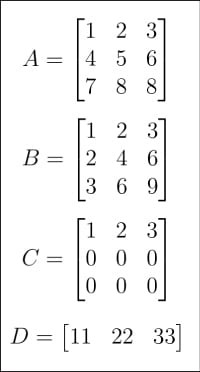 Figure 1: Matrix A, B, C, D
Figure 1: Matrix A, B, C, D
After understanding the history of artificial intelligence, it is now time to return to the topic of matrices and vectors. I have briefly introduced them in previous articles. This time, we'll delve deeper into the world of the Matrix. First, please look at Figure 1 and Figure 2, which show a total of 8 matrices from A to H. Why are so many matrices needed in artificial intelligence and machine learning tutorials? First of all, as mentioned before, matrices are the core of linear algebra, and linear algebra is not the brain of machine learning, but it is the core of machine learning. Secondly, in the following discussion, each matrix has a specific purpose
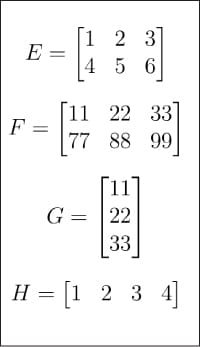 Figure 2: Matrices E, F, G, H
Figure 2: Matrices E, F, G, H
Let Let's look at how matrices are represented and how to get their details. Figure 3 shows how to represent matrix A using NumPy. Although matrices and arrays are not exactly the same, in practical applications we often use them as synonyms
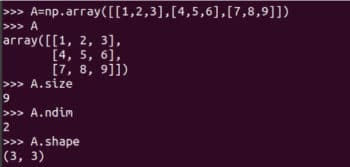 Figure 3: Representing matrix A in NumPy
Figure 3: Representing matrix A in NumPy
I strongly It is recommended that you carefully learn how to use NumPy's array function to create a matrix. Although NumPy also provides the matrix function to create two-dimensional arrays and matrices. But it will be deprecated in the future, so its use is no longer recommended. Some details of matrix A are also shown in Figure 3 . A.size tells us the number of elements in the array. In our case it's 9. Code A.nidm represents the dimension of the array. It is easy to see that matrix A is two-dimensional. A.shape represents the order of matrix A. The order of matrix is the number of rows and columns of the matrix. While I won't explain it further, you need to be aware of the size, dimension, and order of your matrices when using the NumPy library. Figure 4 shows why the size, dimension, and order of a matrix should be carefully identified. Small differences in how an array is defined can result in differences in its size, dimensionality, and order. Therefore, programmers should pay special attention to these details when defining matrices.
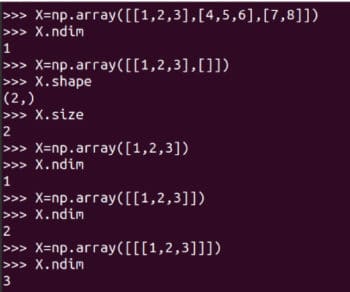 Figure 4: Array size, dimension and order
Figure 4: Array size, dimension and order
Now let’s do some basic matrix operations. Figure 5 shows how matrices A and B are added. NumPy provides two methods for adding matrices, the add function and the operator. Note that only matrices of the same order can be added. For example, two 4 × 3 matrices can be added, but a 3 × 4 matrix and a 2 × 3 matrix cannot be added. However, since programming is different from mathematics, NumPy does not actually follow this rule. Figure 5 also shows adding matrices A and D. Remember, this kind of matrix addition is mathematically illegal. One is called broadcasting broadcasting
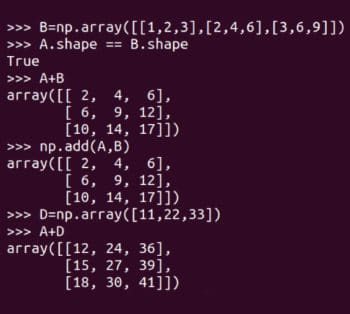 Re-expression: Figure 5: Matrix summation
Re-expression: Figure 5: Matrix summation
Re-expression: Figure 5: Matrix summation
A.shape == B.shape
The broadcast mechanism is not omnipotent. If you try to add matrices D and H, an operation error will occur.
当然除了矩阵加法外还有其它矩阵运算。图 6 展示了矩阵减法和矩阵乘法。它们同样有两种形式,矩阵减法可以由 subtract 函数或减法运算符 - 来实现,矩阵乘法可以由 matmul 函数或矩阵乘法运算符 @ 来实现。图 6 还展示了 逐元素乘法element-wise multiplication 运算符 * 的使用。请注意,只有 NumPy 的 matmul 函数和 @ 运算符执行的是数学意义上的矩阵乘法。在处理矩阵时要小心使用 * 运算符。
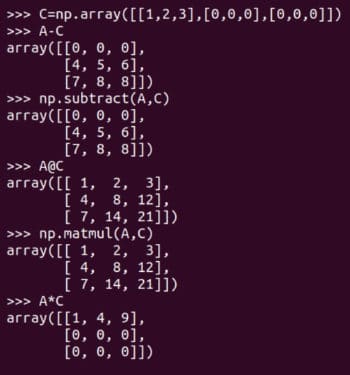 图 6:更多矩阵运算
图 6:更多矩阵运算
对于一个 m x n 阶和一个 p x q 阶的矩阵,当且仅当 n 等于 p 时它们才可以相乘,相乘的结果是一个 m x q 阶矩的阵。图 7 显示了更多矩阵相乘的示例。注意 E@A 是可行的,而 A@E 会导致错误。请仔细阅读对比 D@G 和 G@D 的示例。使用 shape 属性,确定这 8 个矩阵中哪些可以相乘。虽然根据严格的数学定义,矩阵是二维的,但我们将要处理更高维的数组。作为例子,下面的代码创建一个名为 T 的三维数组。
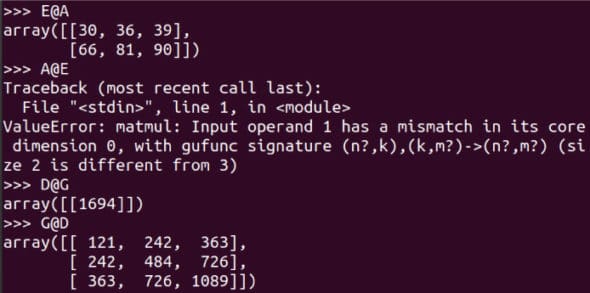 图 7:更多矩阵乘法的例子
图 7:更多矩阵乘法的例子
T = np.array([[[11,22], [33,44]], [[55,66], [77,88]]])
Pandas
到目前为止,我们都是通过键盘输入矩阵的。如果我们需要从文件或数据集中读取大型矩阵并处理,那该怎么办呢?这时我们就要用到另一个强大的 Python 库了——Pandas。我们以读取一个小的 CSV (逗号分隔值comma-separated value)文件为例。图 8 展示了如何读取 cricket.csv 文件,并将其中的前三行打印到终端上。在本系列的后续文章中将会介绍 Pandas 的更多特性。
 图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件
矩阵的秩
需要进行改写的内容是:矩阵的秩
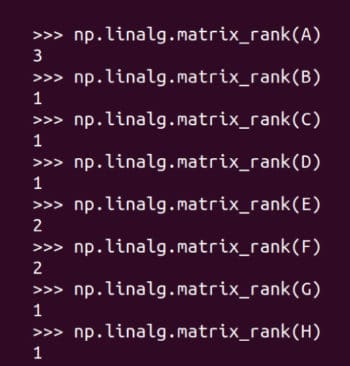 Figure 9: Finding the rank of the matrix
Figure 9: Finding the rank of the matrix
This is the end of this content. In the next article, we will expand the library of tools so that they can be used to develop artificial intelligence and machine learning programs. We will also discuss neural network, supervised learning, unsupervised learning in more detail
The above is the detailed content of Exploring the History and Matrix of Artificial Intelligence: Artificial Intelligence Tutorial (2). For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1376
1376
 52
52
 Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
This site reported on June 27 that Jianying is a video editing software developed by FaceMeng Technology, a subsidiary of ByteDance. It relies on the Douyin platform and basically produces short video content for users of the platform. It is compatible with iOS, Android, and Windows. , MacOS and other operating systems. Jianying officially announced the upgrade of its membership system and launched a new SVIP, which includes a variety of AI black technologies, such as intelligent translation, intelligent highlighting, intelligent packaging, digital human synthesis, etc. In terms of price, the monthly fee for clipping SVIP is 79 yuan, the annual fee is 599 yuan (note on this site: equivalent to 49.9 yuan per month), the continuous monthly subscription is 59 yuan per month, and the continuous annual subscription is 499 yuan per year (equivalent to 41.6 yuan per month) . In addition, the cut official also stated that in order to improve the user experience, those who have subscribed to the original VIP
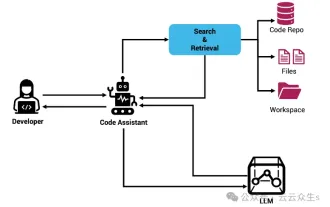 Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Improve developer productivity, efficiency, and accuracy by incorporating retrieval-enhanced generation and semantic memory into AI coding assistants. Translated from EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, author JanakiramMSV. While basic AI programming assistants are naturally helpful, they often fail to provide the most relevant and correct code suggestions because they rely on a general understanding of the software language and the most common patterns of writing software. The code generated by these coding assistants is suitable for solving the problems they are responsible for solving, but often does not conform to the coding standards, conventions and styles of the individual teams. This often results in suggestions that need to be modified or refined in order for the code to be accepted into the application
 Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
To learn more about AIGC, please visit: 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou is different from the traditional question bank that can be seen everywhere on the Internet. These questions It requires thinking outside the box. Large Language Models (LLMs) are increasingly important in the fields of data science, generative artificial intelligence (GenAI), and artificial intelligence. These complex algorithms enhance human skills and drive efficiency and innovation in many industries, becoming the key for companies to remain competitive. LLM has a wide range of applications. It can be used in fields such as natural language processing, text generation, speech recognition and recommendation systems. By learning from large amounts of data, LLM is able to generate text
 Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Large Language Models (LLMs) are trained on huge text databases, where they acquire large amounts of real-world knowledge. This knowledge is embedded into their parameters and can then be used when needed. The knowledge of these models is "reified" at the end of training. At the end of pre-training, the model actually stops learning. Align or fine-tune the model to learn how to leverage this knowledge and respond more naturally to user questions. But sometimes model knowledge is not enough, and although the model can access external content through RAG, it is considered beneficial to adapt the model to new domains through fine-tuning. This fine-tuning is performed using input from human annotators or other LLM creations, where the model encounters additional real-world knowledge and integrates it
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) data set plays a vital role in promoting natural language processing (NLP) research. High-quality QA data sets can not only be used to fine-tune models, but also effectively evaluate the capabilities of large language models (LLM), especially the ability to understand and reason about scientific knowledge. Although there are currently many scientific QA data sets covering medicine, chemistry, biology and other fields, these data sets still have some shortcomings. First, the data form is relatively simple, most of which are multiple-choice questions. They are easy to evaluate, but limit the model's answer selection range and cannot fully test the model's ability to answer scientific questions. In contrast, open-ended Q&A
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing
 SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
Editor | KX In the field of drug research and development, accurately and effectively predicting the binding affinity of proteins and ligands is crucial for drug screening and optimization. However, current studies do not take into account the important role of molecular surface information in protein-ligand interactions. Based on this, researchers from Xiamen University proposed a novel multi-modal feature extraction (MFE) framework, which for the first time combines information on protein surface, 3D structure and sequence, and uses a cross-attention mechanism to compare different modalities. feature alignment. Experimental results demonstrate that this method achieves state-of-the-art performance in predicting protein-ligand binding affinities. Furthermore, ablation studies demonstrate the effectiveness and necessity of protein surface information and multimodal feature alignment within this framework. Related research begins with "S
 Laying out markets such as AI, GlobalFoundries acquires Tagore Technology's gallium nitride technology and related teams
Jul 15, 2024 pm 12:21 PM
Laying out markets such as AI, GlobalFoundries acquires Tagore Technology's gallium nitride technology and related teams
Jul 15, 2024 pm 12:21 PM
According to news from this website on July 5, GlobalFoundries issued a press release on July 1 this year, announcing the acquisition of Tagore Technology’s power gallium nitride (GaN) technology and intellectual property portfolio, hoping to expand its market share in automobiles and the Internet of Things. and artificial intelligence data center application areas to explore higher efficiency and better performance. As technologies such as generative AI continue to develop in the digital world, gallium nitride (GaN) has become a key solution for sustainable and efficient power management, especially in data centers. This website quoted the official announcement that during this acquisition, Tagore Technology’s engineering team will join GLOBALFOUNDRIES to further develop gallium nitride technology. G



