Calculate the intersection of the square of the curve y=x and the straight line x=1 in Java using recursion

Use the recursive method in java to calculate the square of the curve y x and the curved edge surrounded by the straight line x 1 x axis

public class Util {

public static void main(String[] args) {

System.out.println(getMj(2000));

}

public static double calculateArea(double n){

if(n==1){

return 1.0;

}else{

double r = (n-1) * (n-1) * (n 1) * (2*n 1) / (n * n * n * (2*n-1));

return r*getMj(n-1);

}

}

}

The premise of the recursive algorithm is to understand its general formula. 2000 means dividing the curved triangle into 2000 rectangles. The specific principle can be seen in the figure below:

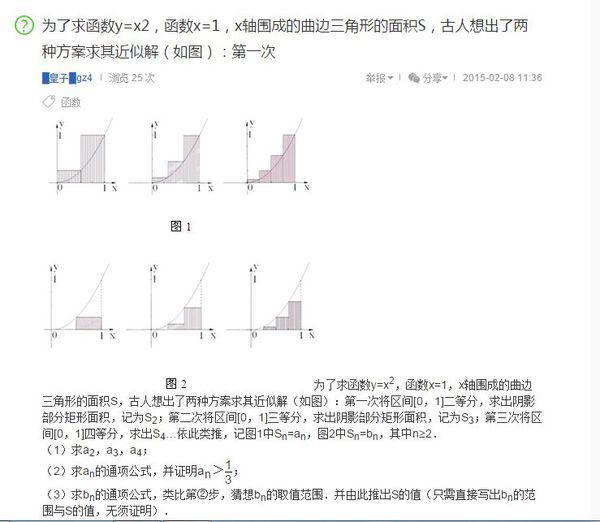
Using the algorithm of Figure 1:

an=(n 1)(2n 1) /6n^2

The simple way to write it is as follows:

public class Util {

public static void main(String[] args) {

System.out.println(getMj(100000));

}

public static double calculateArea(double n){

return (n 1)*(2*n 1)/(6*n*n);

}

}

java recursion problem

(1) Recursion is calling itself in a procedure or function;

(2) When using a recursive strategy, you must ensure that there is a clear recursion end condition, also known as the recursive exit.

Recursive algorithms are generally used to solve three types of problems:

(1)The definition of data is recursively defined. (Fibonacci function)

(2) The problem solution is implemented according to the recursive algorithm. (Traceback)

(3) The structural form of data is defined recursively.

The following example calculates the factorial of n recursively.

public class Test {

public static int factorial(int n) {

if(n == 0){

return 1;

}else{

return n * factorial(n-1);

}

}

public static void main(String[] args) {

System.out.println(factorial(3));

}

}

The recursive algorithm of half search in java data structure hopes for expert guidance!

package souce;

public class Search {

public static boolean binarySearch(int[] a, int x, int left, int right) { // Main method of binary search // ... }

if (x == a[left] || x == a[right]) { return true; // Found, return true }

If the result of (right-left) is a negative number, it means that the value on the right is smaller than the value on the left.

int mid = (left right)/2; //otherwise: two points

if(x == a[mid]) return true; // Find the middle element and return true

else{ //otherwise

If x is greater than the middle element, return the binary search function (binarySearch) and continue to search for x in the right half of the array (a), that is, binarySearch(a,x,mid 1,right). This can narrow the search scope and improve search efficiency.

else return binarySearch(a, x, left, mid-1); // If the target value is less than the middle element, continue searching in the left half.

}

}

public static final int[] sort(int[] a) { // This is a method used to sort an array of integers // You can use any sorting algorithm, such as bubble sort, insertion sort, selection sort, quick sort, etc. // Here we use bubble sort to sort the array for (int i = 0; i a[j 1]) { // Swap element positions int temp = a[j];

for (int i = 0; i

for (int j = 0; j

if(a[i]

swap(a,i,j);

}

}

}

return a;

}

private static void swap(int[] a, int i, int j) { //Define a private static function swap to swap the positions of elements subscripted i and j in array a

int temp = a[i];

a[i] = a[j];

a[j] = temp;

}

public static void print(int[] a) { //Print function for (int i = 0; i

System.out.println();

for (int i = 0; i

System.out.print(a[i]);

if(i!=a.length-1) { System.out.print(","); }

}

System.out.println();

}

public static void main(String[] args) { //Test Methods

int[] a = {90, 12, 21, 32, 51, 78, 87, 98}; is an array containing 8 integers.

print(sort(a));

System.out.println(binarySearch(sort(a), 40, 0, a.length-1)); is a code used to binary search for elements with a value of 40 in the sorted array a.

}

}

The above is the detailed content of Calculate the intersection of the square of the curve y=x and the straight line x=1 in Java using recursion. For more information, please follow other related articles on the PHP Chinese website!