html5 Canvas drawing tutorial (6)—arcTo method for drawing curves in canvas_html5 tutorial skills

The previous article talked about the arc method of canvas, and this article talks about the arcTo method related to it.
arc and arcTo are similar from their names. arcTo is also a method of drawing curves, and the curve he draws is also an arc of a perfect circle. But his parameters are simply incompatible with arc~
ctx.arcTo(x1,y1,x2,y2,radius); The parameters of arcTo include two points, and these two points do not represent the center of the circle. Point, only the last parameter is the radius of the circle, indicating that arcTo has some relationship with the circle.
There are very few articles about arcTo on the Internet, and I finally found one from a foreign country; and there are no intuitive tools for canvas drawing, so I can only rely on guessing. arcTo made me guess for a long time. .
For intuitive description, I adopted an auxiliary method: wherever arcTo is drawn, I also use lineTo to draw the corresponding points to see their relationship. Just draw auxiliary lines.

Copy code

The code is as follows:

var x0=100,
y0 =400,
x1 = 500,
y1 = 400,
x2 = 450,
y2 = 450;
ctx.beginPath();
ctx.moveTo(x0,y0 );
ctx.strokeStyle = "#f00";
ctx.lineWidth = 2;
ctx.arcTo(x1,y1,x2,y2,20);
ctx.stroke();
ctx.beginPath();
ctx.strokeStyle = "rgba(0,0,0,0.5)";
ctx.lineWidth = 1;
ctx.moveTo(x0,y0);
ctx.lineTo(x1,y1);
ctx.fillText('x1,y1',x1 10,y1 10)
ctx.lineTo(x2,y2);
ctx.fillText( 'x2,y2',x2 10,y2)
ctx.stroke();

It seems like a lot of code, but it is actually very simple. I used a few variables to save the coordinate values, and the rest were canvas operations.
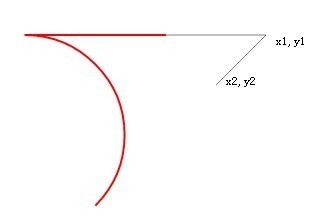
Variable description: x0, y0 are the coordinates of the starting point, x1, y1 are the coordinates of the first point, x2, y2 are the coordinates of the second point. The straight line drawn by lineTo is a translucent 1px black line, and the line drawn by arcTo is a 2px red line.
Refresh the page and you will see the picture below.

I have to say that this red line looks like a hook.
Then the rule of arcTo is found. It actually passes through the starting point, the first point, and the two straight lines at the second point, forming an included angle, and these two lines are also tangents to the parameter circle.
The radius of the circle determines where the circle will be tangent to the line. Just like a ball rolling into a blind spot, the smaller the ball, the farther it rolls in and closer to the dead spot; the opposite is true for a larger ball.
This is a very serious academic issue, please don’t be YY.
Let’s make the ball bigger!

Copy code

The code is as follows:

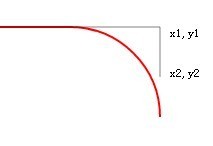
ctx.arcTo(x1,y1,x2 ,y2,50); //Change the radius to 50

As shown in the picture, you can see that the arc has become very large and is not even tangent to the straight line.
Of course, in fact they are still tangent, because the tangent line extends infinitely.
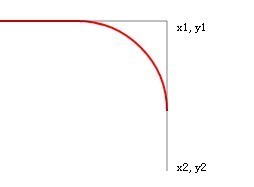
We continue to explore, continue to make the circle larger, and shorten the distance between the starting point and the first point.

Copy code

The code is as follows:

var x0=400; //Start point x The coordinates change from 100 to 400
...
ctx.arcTo(x1,y1,x2,y2,100); //The radius of the circle increases to 100 and then you will see such a strange shape.

It was originally a hook, but now it was bent abruptly, and even in the opposite direction! It's a bit like a wine bottle rack.
However, please note that this circle is still tangent to the two lines! It’s just that now the length of the two lines cannot meet the circle! He has extended both lines wirelessly!
When will this hook handle be reversed? If you are good at geometry, you can try to understand the tangent equation between a point and a circle.
There is a very important point in the arcTo method. This important point is (x1, y1) in the code. As long as its distance to the tangent point of the circle exceeds its distance to the starting point (x0, y0), A reversal will occur.
We can see from the picture that the coordinates of the point (x2, y2) can change infinitely. As long as it is always a point on the tangent line, then when the radius of the circle remains unchanged, the graph drawn by arcTo Nothing will change. This requires special attention.
Let me use my knowledge of geometry that is not available on the table to verify this proposition. To facilitate calculation, I first change the angle between the two lines to 90 degrees.

Copy code

The code is as follows:

var x0=100,
y0=400,
x1 = 500,
y1 = 400,
x2 = 500,
y2 = 450;

After the change, it opens at 90 degrees! We keep the radius of the ball constant. After refresh:

We make y2 larger, that is, extend a tangent line and turn it into 550. After refreshing:

The tangent line is extended, but the red line drawn by arcTo has no change.