 Computer Tutorials
Computer Tutorials
 Computer Knowledge
Computer Knowledge
 How to use the phase angle φ in the trigonometric function y=Asin(wx+φ)
How to use the phase angle φ in the trigonometric function y=Asin(wx+φ)
How to use the phase angle φ in the trigonometric function y=Asin(wx+φ)
What about φ in trigonometric function y Asinwx φ
1. Key point method:
When determining the φ value, consider the intersection of the function y=Asin(ωx φ) B and the x-axis. We need to find the abscissa of the point that initially intersects the x-axis, that is, let ωx φ=0. In this way, the value of φ can be determined. In order to choose the correct point to substitute into the analytical formula, we need to pay attention to which point in the "five-point method" the point belongs to. In the "five-point method", we choose the "first point", which refers to the point where the image intersects the x-axis when it rises. Therefore, ωx φ=0 at this time. Please note that your answer cannot exceed 112 words.
When the "maximum point" (that is, the "peak point" of the image)
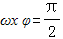
When the "minimum point" (that is, the "valley point" of the image)
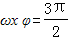
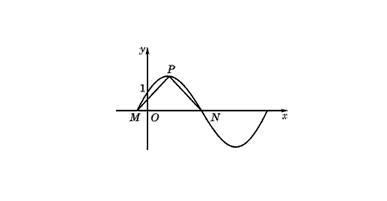
2. Substitution method:
The values of A, ω and B can be determined by substituting known points into the equation or solving for the intersection of the image and the straight line. Pay attention to the intersection location.
Extended information:
Method of monotonicity of trigonometric function y=Asin (ωx φ):
1. We can understand the monotonicity of the function y=Asin (ωx φ) from the perspective of composite functions. The monotonicity of a composite function is determined by both the inner function and the outer function.
If the monotonicity of the inner function and the outer function is the same within a certain interval, the composite function is an increasing function. If the monotonicity of the inner function and the outer function is opposite within a certain interval, the composite function is a decreasing function. In short, both increase and decrease.
2. The image of function y=Asin (ωx φ) is obtained by the function y=sinx through stretching and translation transformation. The monotonicity of the function y=Asin (ωx φ) is also solved based on the function y=sinx.
The function y=Asin (ωx φ) can be seen as a composite of the function y=sint and the function t=ωx φ. The function t=ωx φ is a linear function, and its monotonicity is determined by the sign of ω.
So we only need to regard (ωx φ) as a whole and substitute it into the monotonic interval of y=sint.
For example, the monotonically increasing interval of function y=sint is [-(π/2) 2kπ, (π/2) 2kπ], then we can replace t as a whole with ωx φ, that is, -(π/2) 2kπ≤ ωxφ≤(π/2) 2kπ.
We only need to solve the inequality-(π/2) 2kπ≤(ωx φ)≤(π/2) 2kπ to get the monotonic interval of the function y=Asin(ωx φ).
3. In order to reduce the difficulty of analysis, we generally use the induction formula to change ω in the function y=Asin (ωx φ) to a positive number, so that we can ensure that the linear function t=ωx φ is on the real number set. increasing function.
We know from the properties of composite functions that if we want the monotonic increase (decrease) interval of the function y=Asin (ωx φ), we will bring the whole (ωx φ) into the monotonic increase (decrease) interval of the function y=sint, and then combine it The positive and negative of A, and finally solve the range of x. The solved x range is the monotonic interval of the function y=Asin (ωx φ).
Reference source: Encyclopedia - Trigonometric Functions
Slope formula of straight line
The formula for calculating the slope of a straight line: k=(y2-y1)/(x2-x1)
The tangent of the angle formed by a straight line and the X-axis on the right.
k=tanα=(y2-y1)/(x2-x1)or(y1-y2)/(x1-x2)
When the slope of the straight line L exists, for the linear function y=kx b (slope-intercept form), k is the slope of the function image (straight line).
Extended information
When the slope of straight line L does not exist, the slope-intercept formula y=kx b when k=0 y=b
When the slope of straight line L exists, the point slope formula y2—y1=k(X2—X1),
When the straight line L has a non-zero intercept on the two coordinate axes, there is an intercept formula X/a y/b=1
For any point on any function, its slope is equal to the angle between its tangent and the positive direction of the x-axis, that is, tanα
Slope calculation: ax by c=0, k=-a/b.
Line slope formula: k=(y2-y1)/(x2-x1)
The product of the slopes of two perpendicular intersecting straight lines is -1:k1*k2=-1.
When k>0, the greater the angle between the straight line and the x-axis, the greater the slope; when k
The above is the detailed content of How to use the phase angle φ in the trigonometric function y=Asin(wx+φ). For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 ENE SYS Maintenance: Tips and Tricks to Keep Your System Running Smoothly
Mar 07, 2025 pm 03:09 PM
ENE SYS Maintenance: Tips and Tricks to Keep Your System Running Smoothly
Mar 07, 2025 pm 03:09 PM
This article provides practical tips for maintaining ENE SYS systems. It addresses common issues like overheating and data corruption, offering preventative measures such as regular cleaning, backups, and software updates. A tailored maintenance s
 How to Solve Windows Error Code "INVALID_DATA_ACCESS_TRAP" (0x00000004)
Mar 11, 2025 am 11:26 AM
How to Solve Windows Error Code "INVALID_DATA_ACCESS_TRAP" (0x00000004)
Mar 11, 2025 am 11:26 AM
This article addresses the Windows "INVALID_DATA_ACCESS_TRAP" (0x00000004) error, a critical BSOD. It explores common causes like faulty drivers, hardware malfunctions (RAM, hard drive), software conflicts, overclocking, and malware. Trou
 How do I edit the Registry? (Warning: Use with caution!)
Mar 21, 2025 pm 07:46 PM
How do I edit the Registry? (Warning: Use with caution!)
Mar 21, 2025 pm 07:46 PM
Article discusses editing Windows Registry, precautions, backup methods, and potential issues from incorrect edits. Main issue: risks of system instability and data loss from improper changes.
 How do I manage services in Windows?
Mar 21, 2025 pm 07:52 PM
How do I manage services in Windows?
Mar 21, 2025 pm 07:52 PM
Article discusses managing Windows services for system health, including starting, stopping, restarting services, and best practices for stability.
 Discover How to Fix Drive Health Warning in Windows Settings
Mar 19, 2025 am 11:10 AM
Discover How to Fix Drive Health Warning in Windows Settings
Mar 19, 2025 am 11:10 AM
What does the drive health warning in Windows Settings mean and what should you do when you receive the disk warning? Read this php.cn tutorial to get step-by-step instructions to cope with this situation.
 5 Common Mistakes to Avoid During ENE SYS Implementation
Mar 07, 2025 pm 03:11 PM
5 Common Mistakes to Avoid During ENE SYS Implementation
Mar 07, 2025 pm 03:11 PM
This article identifies five common pitfalls in ENE SYS implementation: insufficient planning, inadequate user training, improper data migration, neglecting security, and insufficient testing. These errors can lead to project delays, system failures
 which application uses ene.sys
Mar 12, 2025 pm 01:25 PM
which application uses ene.sys
Mar 12, 2025 pm 01:25 PM
This article identifies ene.sys as a Realtek High Definition Audio driver component. It details its function in managing audio hardware, emphasizing its crucial role in audio functionality. The article also guides users on verifying its legitimacy
 why won't driver asio.sys load
Mar 10, 2025 pm 07:58 PM
why won't driver asio.sys load
Mar 10, 2025 pm 07:58 PM
This article addresses the failure of the Windows asio.sys audio driver. Common causes include corrupted system files, hardware/driver incompatibility, software conflicts, registry issues, and malware. Troubleshooting involves SFC scans, driver upda





